題目
給你一個數組 points ,其中 points[i] = [xi, yi] 表示 X-Y 平面上的一個點。求最多有多少個點在同一條直線上。
- 示例 1:
輸入:points = [[1,1],[2,2],[3,3]]
輸出:3
- 示例 2:
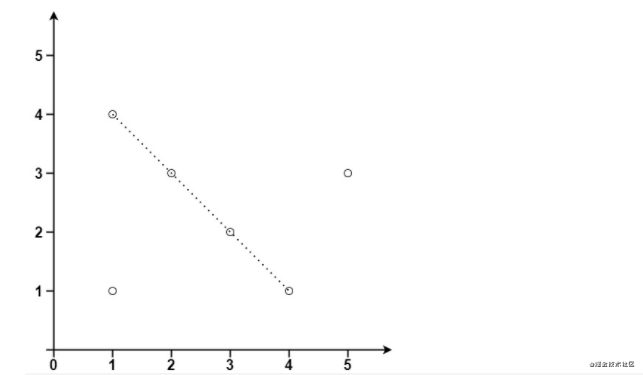
輸入:points = [[1,1],[3,2],[5,3],[4,1],[2,3],[1,4]]
輸出:4
提示:
- 1 <= points.length <= 300
- points[i].length == 2
- -104 <= xi, yi <= 104
- points 中的所有點 互不相同
解題思路
- 遍歷每一個點標i,以點標i為原點向后遍歷后面的所有點標,記作j,計算i與j之間的斜率和截距(因為統一以i為起點,所以不需要計算截距,只需要用斜率就能表示一條直線)
- 使用map記錄斜率,因為都經過點標i,所以相同斜率即為同一條直線上的點,考慮到斜率可能是小數的精度問題,因此將斜率化成最簡分數的形式(使用輾轉相除法求最大公約數),再使用字符串進行表示。最后,斜率相同的直線個數+1(因為一條直線是由兩個點表示的,因此n條直線里面含有n+1個點),就是處于同一直線下的點標數量。
輾轉相除法
做法:用較大數除以較小數,再用出現的余數(第一余數)去除除數,再用出現的余數(第二余數)去除第一余數,如此反復,直到最后余數是0為止。
代碼
class Solution {int gcd(int a, int b) {return b == 0 ? a : gcd(b, a % b);}public int maxPoints(int[][] points) {int n=points.length,res=1;for (int i = 0; i < n; i++) {HashMap<String, Integer> map = new HashMap<>();int x1=points[i][0],y1=points[i][1];int max=0;for (int j = i+1; j < n; j++) {int x2=points[j][0],y2=points[j][1];int a=x1-x2,b=y1-y2;int gcd = gcd(a, b);String key = (a / gcd) + " " + (b / gcd);map.put(key,map.getOrDefault(key,0)+1);max=Math.max(max,map.get(key));}res=Math.max(res,max+1);}return res;}
}















)



