題目
N x N 的棋盤?board 上,按從?1 到 N*N?的數字給方格編號,編號 從左下角開始,每一行交替方向。
例如,一塊 6 x 6 大小的棋盤,編號如下:
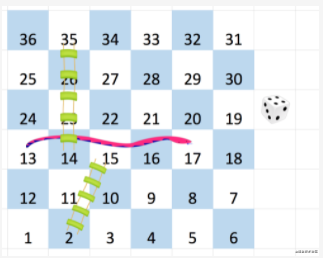
r 行 c 列的棋盤,按前述方法編號,棋盤格中可能存在 “蛇” 或 “梯子”;如果 board[r][c] != -1,那個蛇或梯子的目的地將會是 board[r][c]。
玩家從棋盤上的方格?1 (總是在最后一行、第一列)開始出發。
每一回合,玩家需要從當前方格 x 開始出發,按下述要求前進:
選定目標方格:選擇從編號 x+1,x+2,x+3,x+4,x+5,或者 x+6 的方格中選出一個目標方格 s ,目標方格的編號 <= N*N。
該選擇模擬了擲骰子的情景,無論棋盤大小如何,你的目的地范圍也只能處于區間 [x+1, x+6] 之間。
傳送玩家:如果目標方格 S 處存在蛇或梯子,那么玩家會傳送到蛇或梯子的目的地。否則,玩家傳送到目標方格 S。?
注意,玩家在每回合的前進過程中最多只能爬過蛇或梯子一次:就算目的地是另一條蛇或梯子的起點,你也不會繼續移動。
返回達到方格 N*N 所需的最少移動次數,如果不可能,則返回 -1。
示例:
輸入:[
[-1,-1,-1,-1,-1,-1],
[-1,-1,-1,-1,-1,-1],
[-1,-1,-1,-1,-1,-1],
[-1,35,-1,-1,13,-1],
[-1,-1,-1,-1,-1,-1],
[-1,15,-1,-1,-1,-1]]
輸出:4
解釋:
首先,從方格 1 [第 5 行,第 0 列] 開始。
你決定移動到方格 2,并必須爬過梯子移動到到方格 15。
然后你決定移動到方格 17 [第 3 行,第 5 列],必須爬過蛇到方格 13。
然后你決定移動到方格 14,且必須通過梯子移動到方格 35。
然后你決定移動到方格 36, 游戲結束。
可以證明你需要至少 4 次移動才能到達第 N*N 個方格,所以答案是 4。
解題思路
- 因為棋盤的編號是蛇形的,所以通過蛇形遍歷,可以按編號順序從小到大遍歷一次,當遇到不是-1的點時,使用map記錄該編號下可以跳轉的下一個點
- 使用廣度優先搜索,從編號為1的點開始遍歷,每一步可以從編號 x+1,x+2,x+3,x+4,x+5,或者 x+6 的方格中選出一個目標方格 s,通過map可以查出跳轉到的下一個編號(如果存在蛇或梯子的話)
代碼
class Solution {public int snakesAndLadders(int[][] board) {int n=board.length,cur=1;boolean flag=true;Map<Integer,Integer>map=new HashMap<>();for (int i=n-1;i>=0;i--){if(flag){for (int j=0;j<n;j++,cur++){if(board[i][j]!=-1)map.put(cur,board[i][j]);}flag=false;}else {for (int j=n-1;j>=0;j--,cur++){if(board[i][j]!=-1)map.put(cur,board[i][j]);}flag=true;}}Queue<Integer>queue=new LinkedList<>();queue.add(1);Set<Integer>set=new HashSet<>();set.add(1);int res=0;while (!queue.isEmpty()){int size=queue.size();for (int i=0;i<size;i++){int c=queue.poll();if(c==n*n) return res;for(int k=1;k<=6;k++){int now=c+k;if(map.containsKey(now))now=map.get(now);if(!set.contains(now))queue.add(now);set.add(now);}}res++;}return -1;}
}

)

















