This post is not meant for seasoned statisticians. This is geared towards data scientists and machine learning (ML) learners & practitioners, who like me, do not come from a statistical background.

?他的職位是不是意味著經驗豐富的統計人員。 這是針對數據科學家和機器學習(ML)學習者和從業者的 ，他們和我一樣，并非來自統計背景。

For a person being from a non-statistical background the most confusing aspect of statistics, are the fundamental statistical tests, and when to use which test?. This post is an attempt to mark out the difference between the most common tests and the relevant key assumptions.

對于一個非統計學背景的人來說，統計方面最令人困惑的方面是基本統計檢驗 ，以及何時使用哪種檢驗？ 這篇文章是試圖指出最常見的測試和相關的關鍵假設之間的差異。

目錄 (Table of contents)

1. Terminologies: (KEY TERMINOLOGIES FOR THIS POST)

   術語：( 此職位的主要術語)

2. Statistical Test(Hypothesis Testing)
   統計檢驗(假設檢驗)
3. Statistical Assumptions
   統計假設
4. Parametric tests
   參數測試
5. Parametric test Flowchart
   參數測試流程圖
6. Dealing with non-normal distributions (Non-Parametric tests)
   處理非正態分布(非參數檢驗)

1)術語： (1) TERMINOLIGIES:)

獨立變量和獨立變量 (DEPENDENT AND INDEPENDENT VARIABLES)

An independent variable often called “predictor variable”, is a variable that is being manipulated in order to observe the effect on a dependent variable, sometimes called an outcome/output variable.

通常被稱為“預測變量”的自變量是為了觀察對因變量的影響而被操縱的變量，有時稱為結果/輸出變量。

• Independent variable(s)-> Predictor variable(s)
  自變量->預測變量
• Dependent variable(s) -> Outcome/Output variable(s)
  因變量->結果/輸出變量

變量類型 (TYPES OF VARIABLES)

It is important to distinguish the difference between the type of variables because this plays a key role in determining the correct type of statistical test to adopt. There are two main categories:

區分變量類型之間的差異非常重要，因為這在確定要采用的正確統計檢驗類型中起著關鍵作用。 主要有兩個類別：

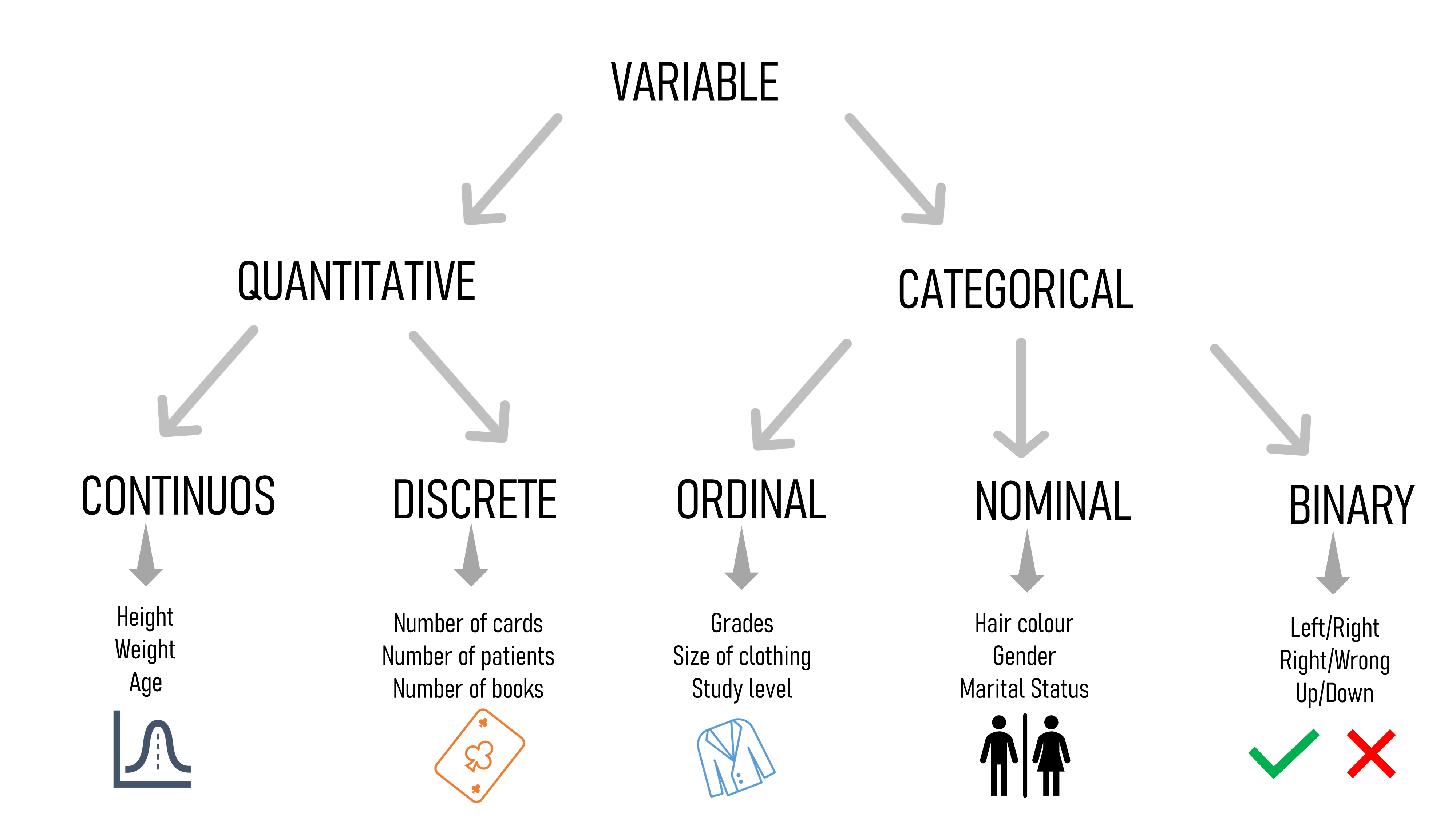
• QUANTITATIVE: express the amounts of things (e.g. the number of cigarettes in a pack). The two different types of quantitative variables are:

  數量 ： 表達物品的數量(例如，一包香煙的數量)。 兩種不同類型的定量變量是：

1. CONTINOUS (a.k.a Ratio): is used to describe measures and can usually be divided into units smaller than one (e.g. 1.50 kg).

   連續 (又稱比率 )：用于描述度量，通常可以劃分為小于一的單位(例如1.50千克)。

2. DISCRETE (a.k.a Interval): is used to describe counts and usually can’t be divided into units smaller than one (e.g. 1 cigarette).

   DISCRETE (又名Interval )：用于描述計數，通常不能分為小于1的單位(例如1支香煙)。

• CATEGORICAL: express groupings of things (e.g. the different type of fruits). The three different types of categorical variables are:

  類別 ： 表達事物的分組(例如，不同類型的水果)。 三種不同類型的類別變量是：

1. ORDINAL: represent data with an order (e.g. rankings).

   序數：表示具有順序的數據(例如排名)。

2. NOMINAL: represent group names (e.g. brands or species names).

   名詞：代表組名(例如品牌或品種名稱)。

3. BINARY: represent data with a yes/no or 1/0 outcome (e.g. LEFT or RIGHT).

   BINARY ：表示結果為是/否或1/0的數據(例如，左或右)。

2)統計測試 (2) STATISTICAL TESTS)

Statistics is all about data. Data alone is not interesting. It is the interpretation of the data that we are interested in.

統計信息都是關于數據的。 單獨的數據并不有趣。 它是對我們感興趣的數據的解釋。

In Statistics, one very important thing is statistical testing, if statistics “is the interpretation of the data”, statistical testing can be considered as the “formal procedure for investigating our ideas about the world”.

在統計中，非常重要的一件事是統計測試，如果統計“是對數據的解釋”，則統計測試可以被視為“調查我們對世界的看法的正式程序”。

In other words, whenever we want to make claims about the distribution of data or whether one set of results are different from another set of results, data scientists must rely on hypothesis testing.

換句話說，每當我們要對數據的分布或一組結果是否與另一組結果有所不同時，數據科學家必須依靠假設檢驗。

假設檢驗 (HYPOTHESIS TESTING)

Using Hypothesis Testing, we try to interpret or draw conclusions about the population using sample data, evaluating two mutually exclusive statements about a population to determine which statement is best supported by the sample data.

使用“ 假設檢驗” ，我們嘗試使用樣本數據來解釋或得出有關總體的結論，評估關于總體的兩個互斥陳述，以確定樣本數據最能支持哪種陳述。

假設檢驗有五個主要步驟： (THERE ARE FIVE MAIN STEPS IN HYPOTHESIS TESTING:)

Step 1) State your hypothesis as a Null (Ho) and Alternate (Ha) hypothesis.

步驟1)將您的假設陳述為零(Ho)和替代(Ha)假設。

Step 2) Choose a significance level (also called alpha or α).

步驟2)選擇顯著性水平(也稱為alpha或α)。

Step 3) Collect data in a way designed to test the hypothesis.

步驟3)以旨在檢驗假設的方式收集數據。

Step 4) Perform an appropriate statistical test: compute the p-value and compare from the test to the significance level.

步驟4)執行適當的統計檢驗：計算p值，然后將檢驗與顯著性水平進行比較。

Step 5) Decide whether to “ REJECT ” the null hypothesis(Ho) or “ FAIL TO REJECT ” the null hypothesis(Ho).

步驟5)決定是“拒絕”無效假設(Ho)還是“失敗”無效假設(Ho)。

Note: Though the specific details might vary, the procedure you will use when testing a hypothesis will always follow some version of these steps.

注意 ：盡管具體細節可能有所不同，但是在檢驗假設時將使用的過程將始終遵循這些步驟的某些版本。

If you want to further understand hypothesis testing, I would highly recommend these two great posts on Hypothesis testing.

如果您想進一步了解假設檢驗，我強烈推薦有關假設檢驗的這兩篇好文章。

3)統計假設 (3) STATISTICAL ASSUMPTIONS)

Statistical tests make some common assumptions about the data being tested (If these assumptions are violated then the test may not be valid: e.g. the resulting p-value may not be correct)

統計測試對要測試的數據做出一些通用假設(如果違反了這些假設，則該測試可能無效：例如，得出的p值可能不正確)

1. Independence of observations: the observations/variables you include in your test should not be related(e.g. several tests from a same test subject are not independent, while several tests from multiple different test subjects are independent)

   觀察結果的獨立性 ：您包含在測試中的觀察值/變量不應該相關(例如，來自同一測試對象的多個測試不是獨立的，而來自多個不同測試對象的多個測試是獨立的)

2. Homogeneity of variance: the “variance” within each group is being compared should be similar to the rest of the group variance. If a group has a bigger variance than the other(s) this will limit the test’s effectiveness.

   方差的同質性 ：比較每個組中的“方差”應與其余組方差相似。 如果組的方差大于其他方，這將限制測試的有效性。

3. Normality of data: the data follows a normal distribution, normality means that the distribution of the test is normally distributed (or bell-shaped) with mean 0, with 1 standard deviation and a symmetric bell-shaped curve.

   數據的正態性 ：數據遵循正態分布，正態性表示測試的分布呈正態分布(或鐘形)，平均值為0，標準差為1，鐘形曲線對稱。

4)參數測試 (4) PARAMETRIC TESTS)

Parametric tests are the ones that can only be run with data that stick with the “three statistical assumptions” mentioned above. The most common types of parametric tests are divided into three categories.

參數測試是只能使用符合上述“三個統計假設”的數據運行的測試。 最常見的參數測試類型分為三類。

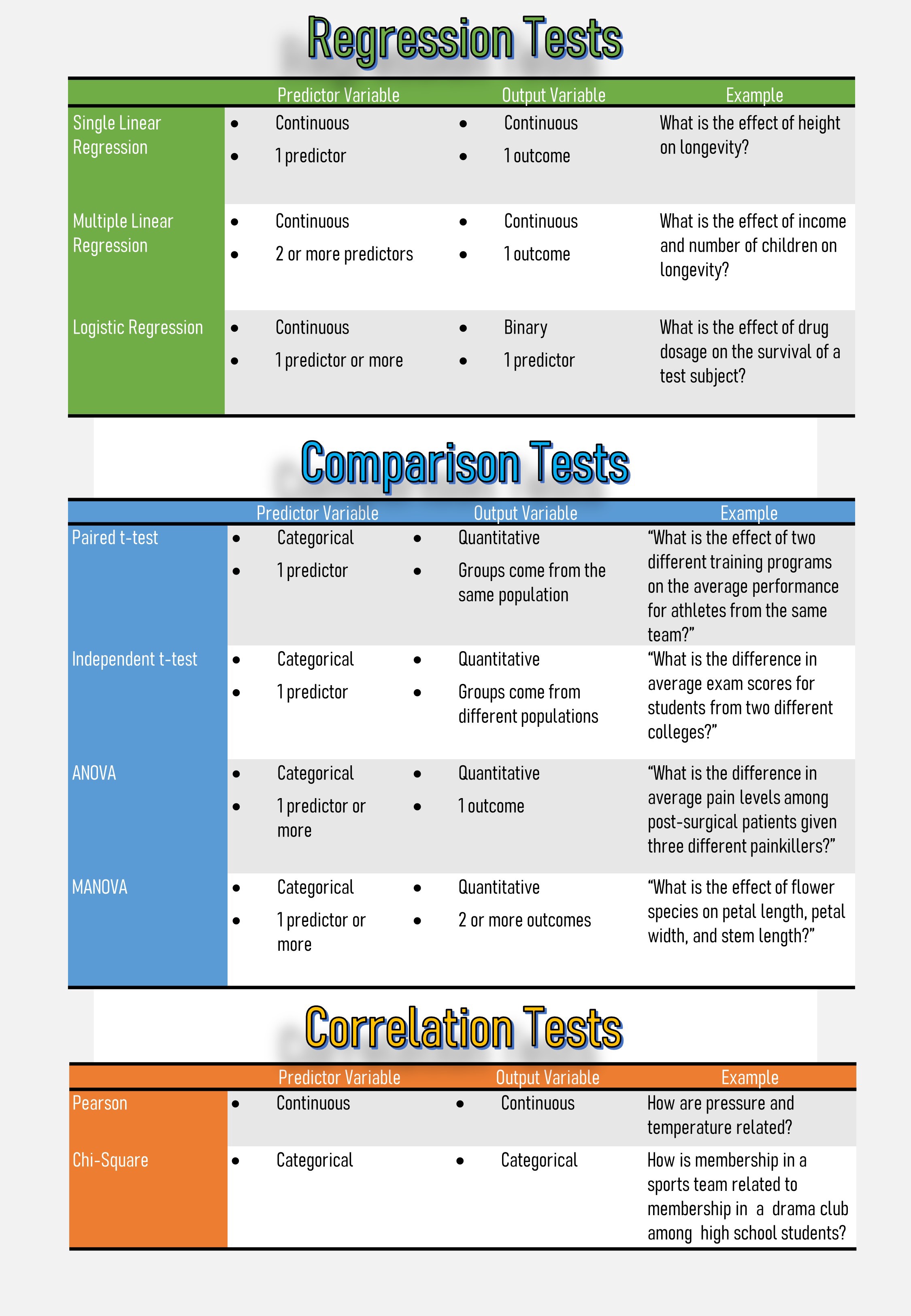
回歸測試： (Regression tests:)

These tests are used test cause-and-effect relationships, if the change in one or more continuous variable predicts change in another variable.

如果一個或多個連續變量的變化預示著另一個變量的變化，則將這些檢驗用于檢驗因果關系 。

• Simple linear regression: tests how a change in the predictor variable predicts the level of change in the outcome variable.

  簡單線性回歸：測試預測變量的變化如何預測結果變量的變化水平。

• Multiple linear regression: tests how changes in the combination of two or more predictor variables predict the level of change in the outcome variable

  多元線性回歸：測試兩個或多個預測變量組合的變化如何預測結果變量的變化水平

• Logistic regression: is used to describe data and to explain the relationship between one dependent (binary) variable and one or more nominal, ordinal, interval or ratio-level independent variable(s).

  Logistic回歸：用于描述數據并解釋一個(二元)變量與一個或多個名義，有序，區間或比率級別的自變量之間的關系。

比較測試： (Comparison tests:)

These tests look for the difference between the means of variables:Comparison of Means.

這些測試尋找變量均值之間的差異：均值比較。

• T-tests are used when comparing the means of precisely two groups (e.g. the average heights of men and women).

  在精確比較兩組的平均值(例如，男性和女性的平均身高)時，使用T檢驗 。

• Independent t-test: Tests the difference between the same variable from different populations (e.g., comparing dogs to cats)

  獨立t檢驗 ：測試來自不同人群的相同變量之間的差異 (例如，比較狗和貓)

• ANOVA and MANOVA tests are used to compare the means of more than two groups or more(e.g. the average weights of children, teenagers, and adults).

  ANOVA和MANOVA檢驗用于比較兩組或以上兩組的均值(例如，兒童，青少年和成人的平均體重)。

關聯測試： (Correlation tests:)

These tests look for an association between variable checking whether two variables are related.

這些測試在變量之間尋找關聯，檢查兩個變量是否相關。

• Pearson Correlation: Tests for the strength of the association between two continuous variables.

  皮爾遜相關：測試兩個連續變量之間關聯的強度。

• Spearman Correlation: Tests for the strength of the association between two ordinal variables (it does not rely on the assumption of normally distributed data)

  Spearman相關性：測試兩個序數變量之間的關聯強度(它不依賴于正態分布數據的假設)

• Chi-Square Test: Tests for the strength of the association between two categorical variables.

  卡方檢驗：測試兩個類別變量之間的關聯強度。

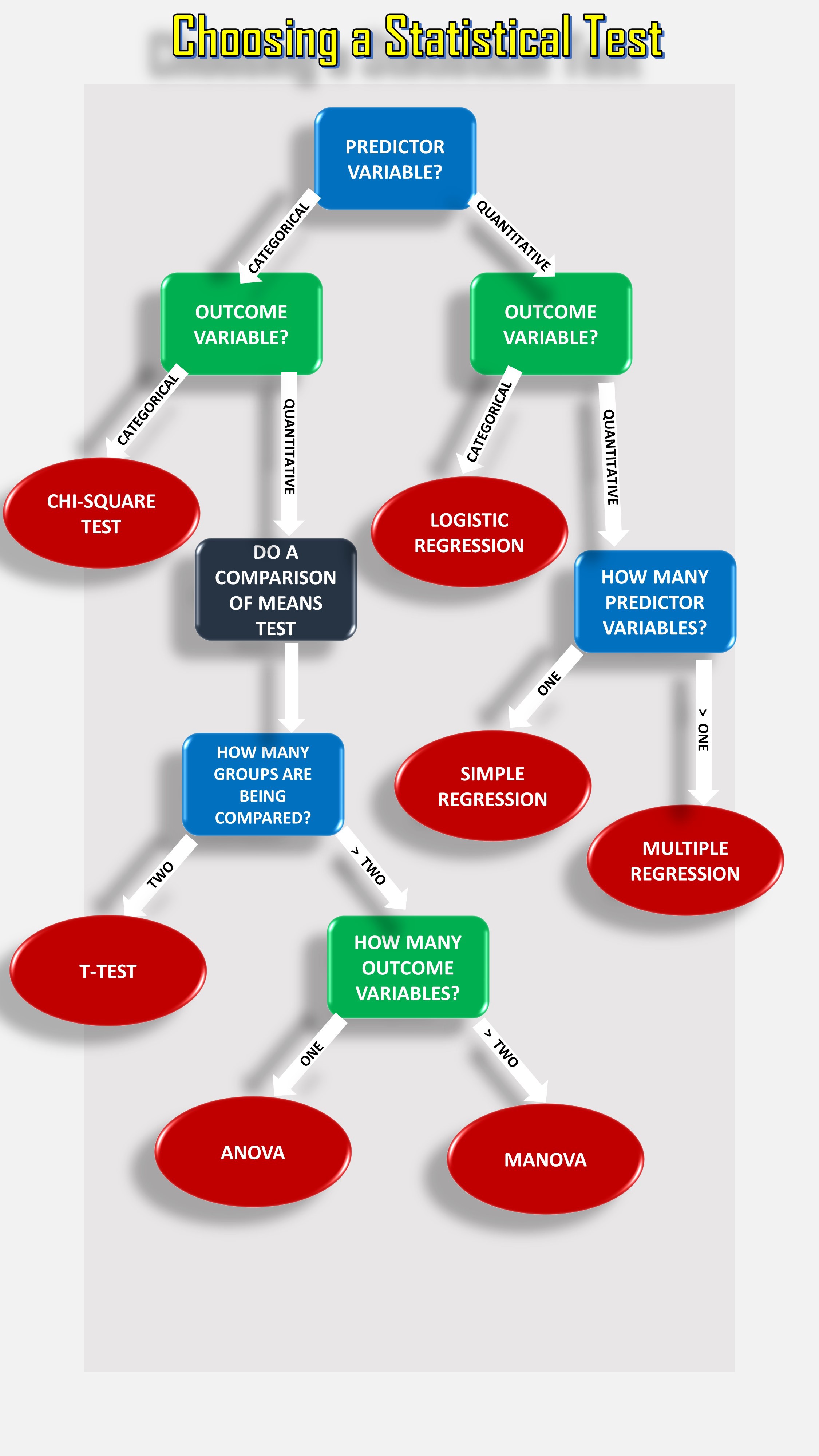
5)流程圖：選擇參數測試 (5) FLOWCHART: CHOOSING A PARAMETRIC TEST)

This flowchart will help you choose among the above described parametric tests. For nonparametric alternatives, check the following section.

該流程圖將幫助您在上述參數測試中進行選擇。 對于非參數替代，請檢查以下部分。

6)處理非正態分布 (6) DEALING WITH NON- NORMAL DISTRIBUTIONS)

Although the normal distribution takes centre part in statistics, many processes follow non-normal distributions. Many datasets naturally fit a non-normal model:

盡管正態分布在統計中占據中心位置，但是許多過程遵循非正態分布。 許多數據集自然適合于非正常模型：

-The number of accidents tends to fit a “Poisson distribution”

-事故數量趨于符合“泊松分布”

-The Lifetimes of products usually fit a “Weibull distribution”.

-產品的使用壽命通常符合“威布爾分布”。

非正態分布的示例 (Example of Non-Normal Distributions)

1. Beta Distribution.
   Beta發行版。
2. Exponential Distribution.
   指數分布。
3. Gamma Distribution.
   伽瑪分布。
4. Inverse Gamma Distribution.
   反伽瑪分布。
5. Log-Normal Distribution.
   對數正態分布。
6. Logistic Distribution.
   物流配送。
7. Maxwell-Boltzmann Distribution.
   Maxwell-Boltzmann分布。
8. Poisson Distribution.
   泊松分布。
9. Skewed Distribution.
   分布偏斜。
10. Symmetric Distribution.
    對稱分布。
11. Uniform Distribution.
    均勻分布。
12. Unimodal Distribution.
    單峰分布。
13. Weibull Distribution.
    威布爾分布。

那么，我們如何處理非正態分布？ (Well then, How do we deal with non-Normal-Distributions?)

When your data is supposed to fit a normal distribution but doesn’t, we could do a few things to handle them:

當您的數據應該符合正態分布但不符合正態分布時，我們可以做一些事情來處理它們：

• We may still be able to run parametric tests if your sample size is large enough (usually over 20 items) and try to interpret the results accordingly.
  如果您的樣本量足夠大(通常超過20個項目)，我們仍然可以運行參數測試，并嘗試相應地解釋結果。
• We may choose to transform the data with different statistical techniques, forcing it to fit a normal distribution.
  我們可能選擇使用不同的統計技術來轉換數據，迫使其適應正態分布。

• If the sample size is small, skewed or if it represents another distribution type, you might run a non-parametric test.

  如果樣本量小，偏斜或代表其他分布類型，則可以運行非參數檢驗 。

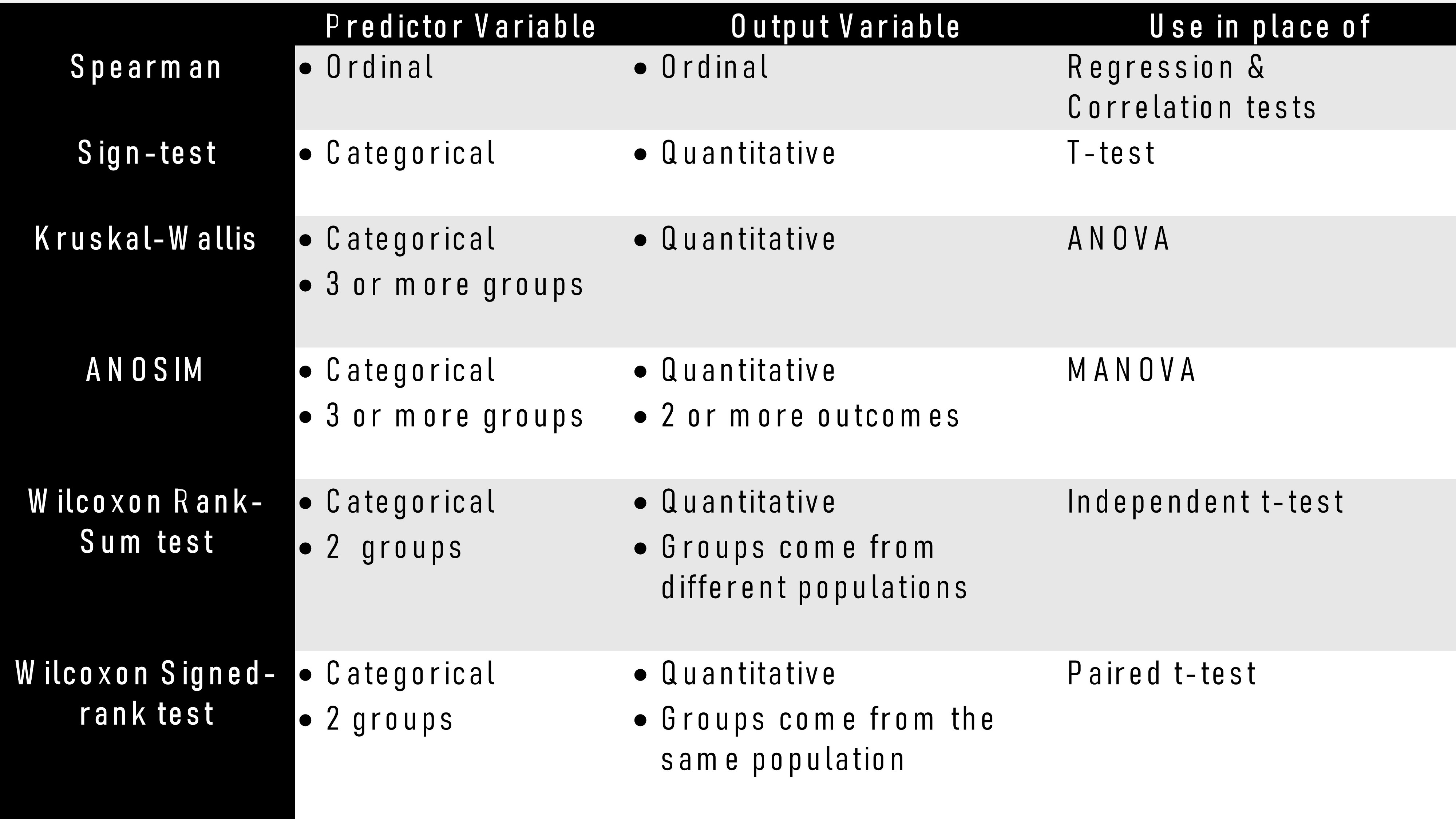
非參數測試 (Non-Parametric Tests)

Non-parametric tests (figure below) don’t make as many assumptions about the data and are useful when one or more of the three statistical assumptions are violated.

非參數檢驗(下圖)對數據的假設不多，當違反三個統計假設中的一個或多個時很有用。

Note that: The inferences that non-parametric tests make aren’t as strong as the parametric tests.

請注意：非參數測試的推論不如參數測試強。

Hope you find this post informative and useful. Please let me know if you have any feedback. Thanks a lot for reading!

希望您發現這篇文章有益和有用。 如果您有任何反饋意見，請告訴我。 非常感謝您的閱讀！