Beginners usually ignore most foundational statistical knowledge. To understand different models, and various techniques better, these concepts are essential. These work as baseline knowledge for various concepts involved in data science, machine learning, and artificial intelligence.

初學者通常會忽略大多數基礎統計知識。 為了更好地理解不同的模型和各種技術，這些概念至關重要。 這些作為數據科學，機器學習和人工智能中涉及的各種概念的基礎知識。

Here is the list of concepts covered in this article.

這是本文涵蓋的概念列表。

1. Measures of central tendency
   集中趨勢的度量
2. Measures of spread
   傳播措施
3. Population & sample
   人口與樣本
4. Central limit theorem
   中心極限定理
5. Sampling & sampling techniques
   采樣與采樣技術
6. Selection Bias
   選擇偏見
7. Correlation & various correlation coefficients
   相關和各種相關系數

Let’s dive in!

讓我們潛入吧！

1-集中趨勢的度量 (1 — Measures of central tendency)

A measure of central tendency is a single value that attempts to describe a set of data by identifying the central position within that set of data. The three most common values used as a measure of center are,

集中趨勢的度量是單個值，該值試圖通過識別數據集中的中心位置來描述該數據集。 用來衡量中心的三個最常見的值是：

— Mean is the average of all the values in data.

—平均值是數據中所有值的平均值。

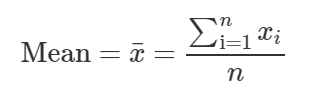
— Median is the middle value in the sorted(ordered) data. Median is a better measure of center than mean as it is not affected by outliers.

—中位數是排序(排序)數據中的中間值。 中值比中心值更好地衡量中心，因為它不受異常值的影響。

— Mode is the most frequent value in the data.

—模式是數據中最頻繁的值。

2-傳播方式 (2 — Measures of spread)

Measures of spread describe how similar or varied the set of observed values are for a particular variable (data item). Measures of spread include the range, quartiles, and the interquartile range, variance, and standard deviation.

傳播量度描述了對于特定變量(數據項)的觀察值集有多相似或多變。 價差的度量包括范圍，四分位數以及四分位數間距，方差和標準差。

— Range is the difference between the smallest value and the largest value in the data.

—范圍是數據中最小值和最大值之間的差。

— Quartiles divide an ordered dataset into four equal parts, and refer to the values of the point between the quarters. The lower quartile (Q1) is the value between the lowest 25% of values and the highest 75% of values. It is also called the 25th percentile.The second quartile (Q2) is the middle value of the data set. It is also called the 50th percentile, or the median.The upper quartile (Q3) is the value between the lowest 75% and the highest 25% of values. It is also called the 75th percentile.

—四分位數將有序數據集分為四個相等的部分，并引用四分之一點之間的點的值。 下四分位數(Q1)是值的最低25％和值的最高75％之間的值。 也稱為第25個百分位數。 第二個四分位數(Q2)是數據集的中間值。 也稱為第50個百分位數，即中位數。 上四分位數(Q3)是值的最低75％和最高25％之間的值。 也稱為第75個百分位。

The interquartile range (IQR) is the difference between the upper (Q3) and lower (Q1) quartiles, and describes the middle 50% of values when ordered from lowest to highest. The IQR is often seen as a better measure of spread than the range as it is not affected by outliers.

四分位數間距(IQR)是上四分位數(Q3)和下四分位數(Q1)之間的差，并描述了從最低到最高順序的中間50％值。 由于IQR不受異常值的影響，因此通常認為IQR比范圍更好。

— The variance of all the data points whose mean is μ, each data point is denoted by Xi, and N number of data points is given by,

-所有的數據點，其平均值μ，每一個數據點是由僖表示的數據點的方差 ，以及N個由下式給出，

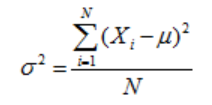
The standard deviation is the square root of the variance. The standard deviation for a population is represented by σ.

標準偏差是方差的平方根。 總體的標準偏差由σ表示。

In datasets with a small spread, all values are very close to the mean, resulting in a small variance and standard deviation. Where a dataset is more dispersed, values are spread further away from the mean, leading to a larger variance and standard deviation.

在具有較小分布的數據集中，所有值都非常接近均值，從而導致較小的方差和標準偏差。 如果數據集更加分散，則值與平均值之間的距離會越來越遠，從而導致較大的方差和標準偏差。

3-人口和樣本 (3 — Population and Sample)

• The population is the entire set of possible data values.

  總體是所有可能的數據值的集合。

• A sample of data set contains a part, or a subset, of a population. The size of a sample is always less than the size of the population from which it is taken.

  數據集樣本包含總體的一部分或子集。 樣本的大小始終小于獲取樣本的人口的大小。

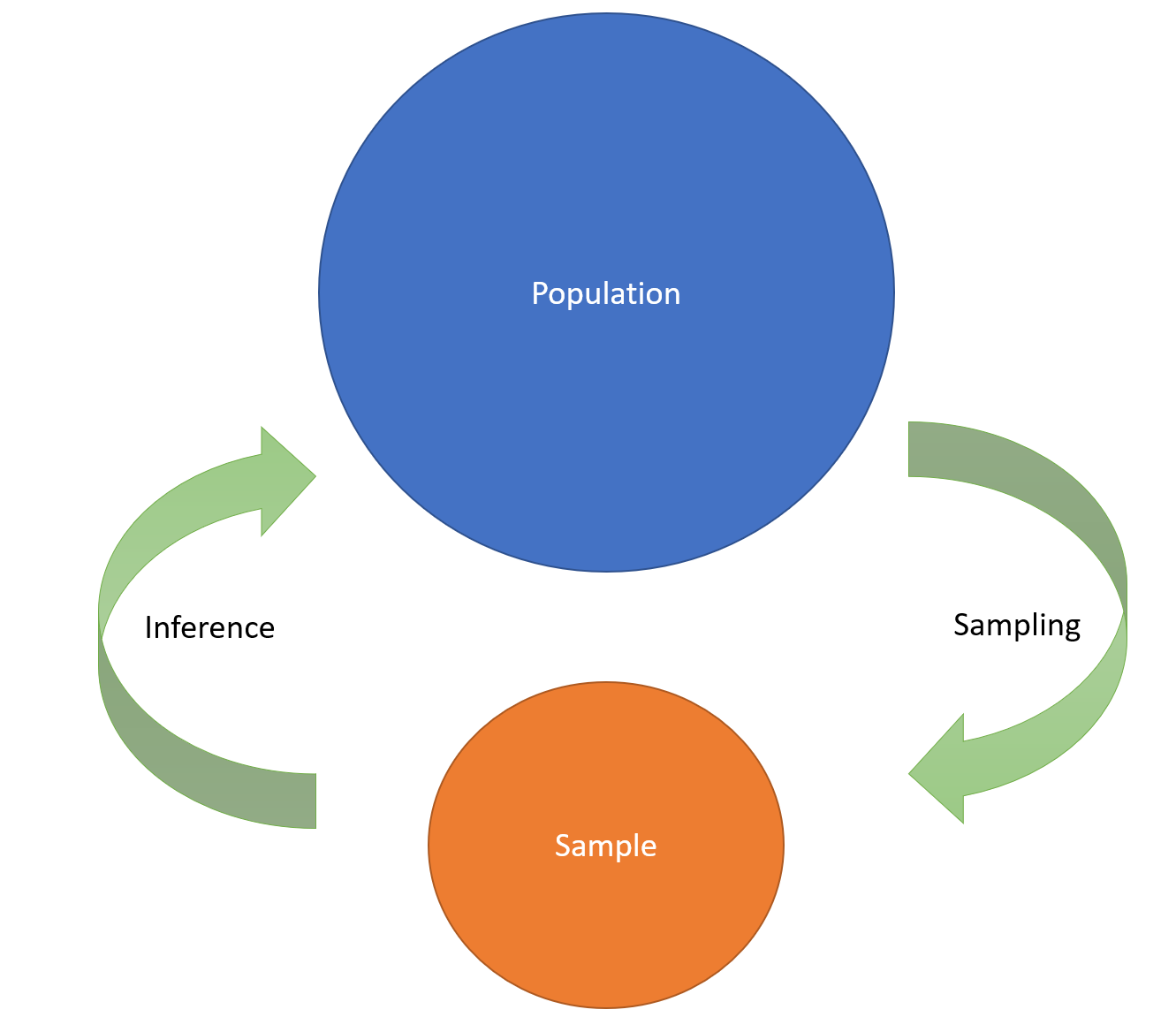
For example, the set of all people of a country is ‘population’ and a subset of people is ‘sample’ which is usually less than the population.

例如， 一個國家的所有人的集合是“ 人口 ”， 一部分人是“ 樣本 ”，通常少于人口。

4 —中心極限定理 (4 — Central Limit Theorem)

Central Limit Theorem is a key concept in probability theory because it implies that probabilistic and statistical methods that work for normal distributions can be applicable to many problems involving other types of distributions.

中心極限定理是概率論中的關鍵概念，因為它暗示適用于正態分布的概率和統計方法可以適用于涉及其他類型分布的許多問題。

CLT states that, “Sampling from a population using a sufficiently large sample size, the mean of the samples, known as the sample mean, will be normally distributed. This is true regardless of the distribution of the population.”

CLT指出：“從使用足夠大樣本量的總體中進行抽樣，樣本均值(即樣本均值)將呈正態分布。 無論人口分布如何，都是如此。”

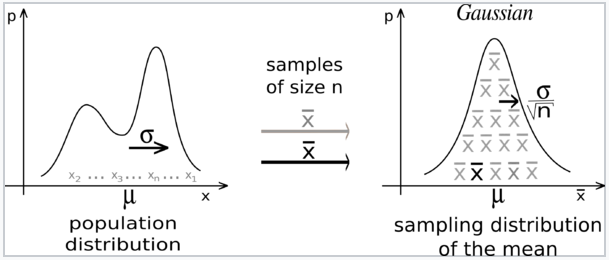
Other acumens from CLT are,

CLT的其他敏銳度是，

• The sample mean converges in probability and almost surely to the expected value of the population mean.
  樣本均值收斂于概率，并且幾乎可以肯定地收斂于總體均值的期望值。
• The variance of the population is the same as the product of variance of the sample and the number of elements in each sample.
  總體方差與樣本方差與每個樣本中元素數量的乘積相同。

5—采樣和采樣技術 (5— Sampling & Sampling techniques)

Sampling is a statistical analysis technique used to select, manipulate, and analyze a representative subset of the data points to identify patterns and trends in the larger data set under observation.

采樣是一種統計分析技術，用于選擇，操作和分析數據點的代表性子集，以識別正在觀察的較大數據集中的模式和趨勢。

There are many different methods for drawing samples from the data; the ideal one depends on the data set and problem in hand. Commonly used sampling techniques are given below,

有很多不同的方法可以從數據中提取樣本。 理想的選擇取決于數據集和手頭的問題。 下面給出了常用的采樣技術，

• Simple random sampling: In this case, each value in the sample is chosen entirely by chance and each value of the population has an equal chance, or probability, of being selected.

  簡單隨機抽樣：在這種情況下，樣本中的每個值完全是由偶然選擇的，總體中的每個值都有相等的被選擇的機會或概率。

• Stratified sampling: In this method, the population is first divided into subgroups (or strata) which share a similar characteristic. It is used when we might reasonably expect the measurement of interest to vary between the different subgroups, and we want to ensure representation from all the subgroups.

  分層抽樣：采用這種方法，首先將總體分為具有相似特征的子組(或階層)。 當我們可能合理地期望感興趣的度量在不同子組之間發生變化，并且我們希望確保所有子組都有代表性時，可以使用它。

• Cluster sampling: In a clustered sample, subgroups of the population are used as the sampling unit, rather than individual values. The population is divided into subgroups, known as clusters, which are randomly selected to be included in the study.

  聚類抽樣：在聚類樣本中，總體的子組用作抽樣單位，而不是單個值。 總體分為亞組，稱為簇，被隨機選擇以納入研究。

• Systematic sampling: Individual values are selected at regular intervals from the sampling frame. The intervals are chosen to ensure an adequate sample size. If you need a sample size n from a population of size x, you should select every x/nth individual for the sample.

  系統采樣：從采樣幀中定期選擇單個值。 選擇間隔以確保足夠的樣本量。 如果需要從數量為x的總體中獲得樣本大小為n ，則應為樣本選擇每個第x / n個人。

6 —選擇偏向 (6 — Selection Bias)

Selection bias (also called Sampling bias) is a systematic error due to a non-random sample of a population, causing some values of the population to be less likely to be included than others, resulting in a biased sample, in which all values are not equally balanced or objectively represented.

選擇偏差(也稱為抽樣偏差)是由于總體的非隨機樣本而導致的系統誤差，導致總體的某些值比其他值更不可能被包含，從而導致偏差樣本，其中所有值都是不能均衡地平衡或客觀地代表。

This means that proper randomization is not achieved, thereby ensuring that the sample obtained is not representative of the population intended to be analyzed.

這意味著無法實現適當的隨機化，從而確保獲得的樣本不代表要分析的總體。

In the general case, selection biases cannot be overcome with statistical analysis of existing data alone. An assessment of the degree of selection bias can be made by examining correlations.

通常，僅通過對現有數據進行統計分析就無法克服選擇偏見。 選擇偏倚程度的評估可以通過檢查相關性來進行。

7 —相關性 (7 — Correlation)

Correlation is simply, a metric that measures the extent to which variables (or features or samples or any groups) are associated with one another. In almost any data analysis, data scientists will compare two variables and how they relate to one another.

簡單來說，相關性是一種度量，用于度量變量(或特征，樣本或任何組)相互關聯的程度。 在幾乎所有數據分析中，數據科學家都將比較兩個變量以及它們之間的關系。

The following are the most widely used correlation techniques,

以下是使用最廣泛的相關技術，

1. Covariance
   協方差
2. Pearson Correlation Coefficient
   皮爾遜相關系數
3. Spearman Rank Correlation Coefficient
   斯皮爾曼等級相關系數

1.協方差 (1. Covariance)

For two samples, say, X and Y, let E(X), E(Y) be the mean values of X, Y respectively, and ‘n’ be the total number of data points. The covariance of X, Y is given by,

對于兩個樣本，例如X和Y ，令E(X)，E(Y)分別為X，Y的平均值，而' n '為數據點的總數。 X，Y的協方差為

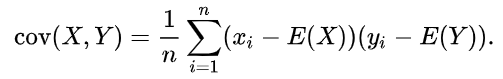
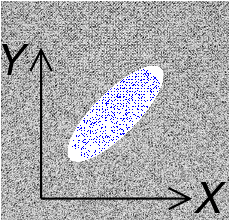
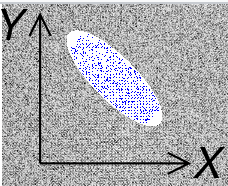
The sign of the covariance indicates the tendency of the linear relationship between the variables.

協方差的符號表示變量之間線性關系的趨勢。

2.皮爾遜相關系數 (2. Pearson Correlation Coefficient)

Pearson Correlation Coefficient is a statistic that also measures the linear correlation between two features. For two samples, X, Y let σX, σY be the standard deviations of X, Y respectively. PCC of X, Y is given by,

皮爾遜相關系數是一種統計數據，還可以測量兩個特征之間的線性相關性。 對于兩個樣本，X，Y分別使σX，σY為X，Y的標準偏差。 X，Y的PCC由下式給出：

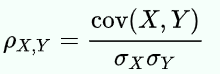
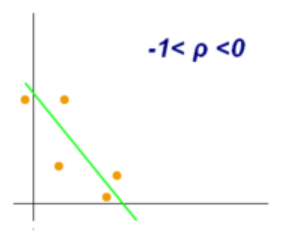
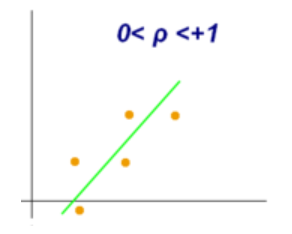
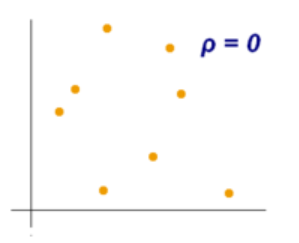
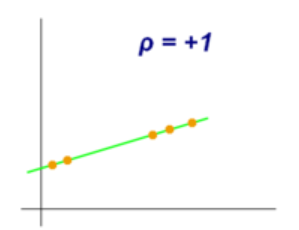
It has a value between -1 and +1.

它的值介于-1和+1之間。

3. Spearman等級相關系數 (3. Spearman Rank Correlation Coefficient)

Spearman Rank Correlation Coefficient (SRCC) assesses how well the relationship between two samples can be described using a monotonic function (whether linear or not) where PCC can assess only linear relationships.

Spearman等級相關系數(SRCC)使用PCC只能評估線性關系的單調函數(無論是否線性 )評估兩個樣本之間的關系描述得如何。

The Spearman rank correlation coefficient between the two samples is equal to the Pearson correlation coefficient between the rank values of those two samples. Rank is the relative position label of the observations within the variable.

兩個樣本之間的Spearman等級相關系數等于這兩個樣本之間的等級值之間的Pearson相關系數 。 等級是變量中觀測值的相對位置標簽。

Intuitively, the Spearman rank correlation coefficient between two variables will be high when observations have a similar rank between the two variables and low when observations have a dissimilar rank between the two variables.

直觀地，當兩個變量之間的觀察值相似時，兩個變量之間的Spearman等級相關系數將較高；而當兩個變量之間的觀察值具有不同等級時，則Spearman等級相關系數將較低。

The Spearman rank correlation coefficient lies between +1 and -1 where

Spearman等級相關系數介于+1和-1之間，其中

• 1 is a perfect positive correlation

  1是完美的正相關

• 0 is no correlation

  0 無相關

• ?1 is a perfect negative correlation

  -1是理想的負相關

To know more about correlation techniques and when to which one, do check that article below.

要了解有關關聯技術以及何時使用哪種技術的更多信息，請檢查以下文章。

Thanks for the read. I am going to write more beginner-friendly posts in the future too. Follow me up on Medium to be informed about them. I welcome feedback and can be reached out on Twitter ramya_vidiyala and LinkedIn RamyaVidiyala. Happy learning!

感謝您的閱讀。 我將來也會寫更多對初學者友好的文章。 跟我上Medium ，以了解有關它們的信息。 我歡迎您提供反饋，可以在Twitter ramya_vidiyala和LinkedIn RamyaVidiyala上與他們聯系 。 學習愉快！