【筆試題心得】排序算法總結整理

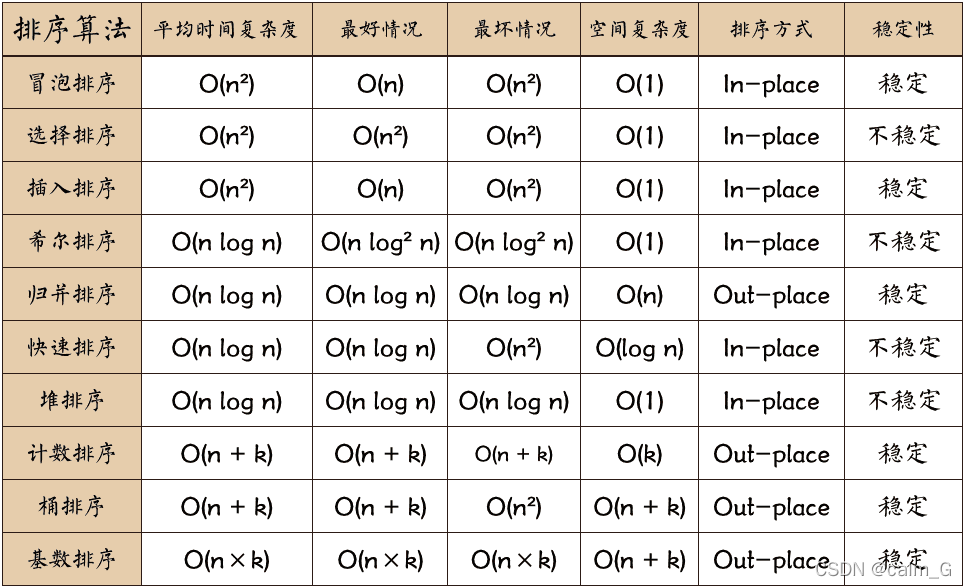
?排序算法匯總

常用十大排序算法_calm_G的博客-CSDN博客

在這里插入圖片描述 ?

?以下動圖參考?十大經典排序算法 Python 版實現（附動圖演示） - 知乎

冒泡排序

排序過程如下圖所示：

比較相鄰的元素。如果第一個比第二個大，就交換他們兩個。
對每一對相鄰元素作同樣的工作，從開始第一對到結尾的最后一對。這步做完后，最后的元素會是最大的數。
針對所有的元素重復以上的步驟，除了最后一個。
持續每次對越來越少的元素重復上面的步驟，直到沒有任何一對數字需要比較。

// arr： 需要排序的數組； length： 數組長度 
//注： int cnt = sizeof(a) / sizeof(a[0]);獲取數組長度
void BubbleSort(int arr[], int length) 
{for (int i = 0; i < length; i++){for (int j = 0; j < length -  i - 1; j++){if (arr[j] > arr[j + 1])swap(arr[j],arr[j+1]);}}
}

選擇排序

排序過程如下圖所示：

在未排序序列中找到最小（大）元素，存放到排序序列的起始位置
從剩余未排序元素中繼續尋找最小（大）元素，然后放到已排序序列的末尾
以此類推，直到所有元素均排序完畢
時間負復雜度：O(n^2)，空間O（1），非穩定排序，原地排序

void selectSort(vector<int>& nums) {int len = nums.size();int minIndex = 0;for (int i = 0; i < len; ++i) {minIndex = i;for (int j = i + 1; j < len; ++j) {if (nums[j] < nums[minIndex]) minIndex = j;}swap(nums[i], nums[minIndex]);}
}

插入排序

排序過程如下圖所示：

從第一個元素開始，該元素可以認為已經被排序

取出下一個元素，在已經排序的元素序列中從后向前掃描

如果該元素（已排序）大于新元素，將該元素移到下一位置

重復步驟3，直到找到已排序的元素小于或者等于新元素的位置

將新元素插入到該位置后

重復步驟2~5

void insertionSort(vector<int>& a, int n) {//{ 9,1,5,6,2,3 }for (int i = 1; i < n; ++i) {if (a[i] < a[i - 1]) {   //若第i個元素大于i-1元素，直接插入。小于的話，移動有序表后插入int j = i - 1;int x = a[i];     //復制為哨兵，即存儲待排序元素//a[i] = a[i - 1];           //先后移一個元素，可以不要這一句，跟循環里面的功能重復了while (j >= 0 && x < a[j]) {   //查找在有序表的插入位置,還必須要保證j是>=0的 因為a[j]要合法a[j + 1] = a[j];j--;     //元素后移}a[j + 1] = x;     //插入到正確位置}}
}

快速排序

?排序過程如下圖所示：

動圖看起來有點復雜，下面放一個分解圖https://blog.csdn.net/qq_38082146/article/details/115453732

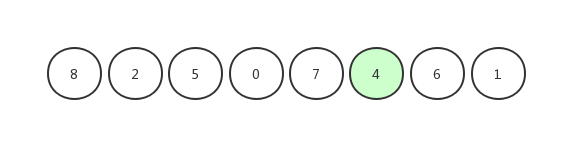
我們以[ 8，2，5，0，7，4，6，1 ]這組數字為例來進行演示

首先，我們隨機選擇一個基準值（雖然圖中選擇了隨機元素，但是一般上會以第一個元素為基準值）：

快速排序1

與其他元素依次比較，大的放右邊，小的放左邊：

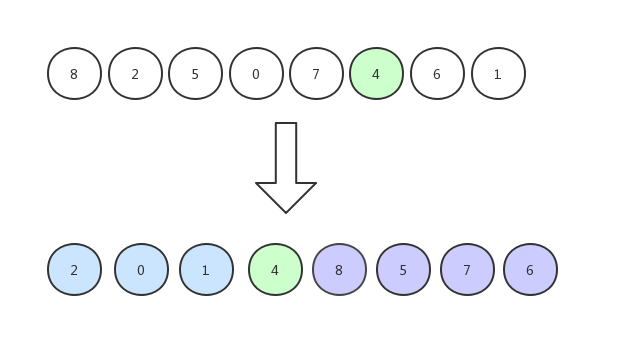
快速排序2

然后我們以同樣的方式排左邊的數據：

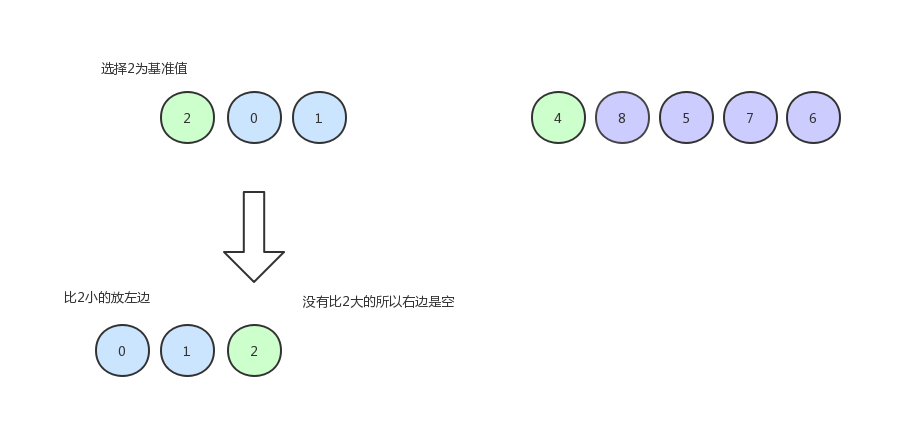
快速排序3

繼續排 0 和 1 ：

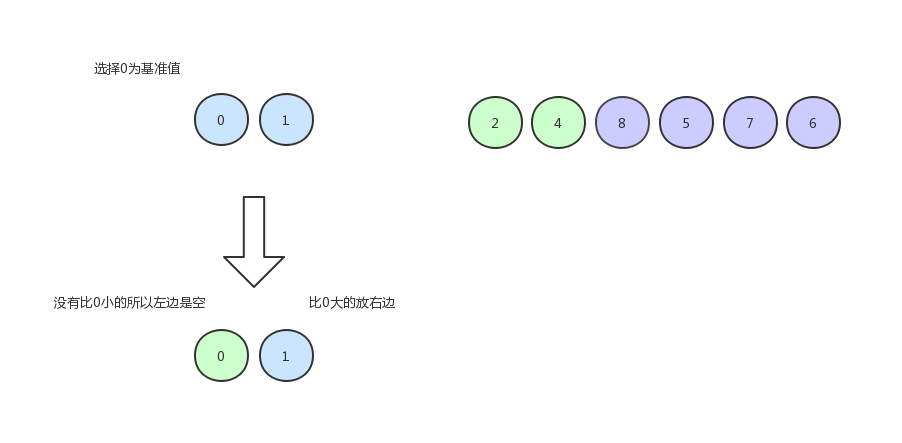
快速排序4

由于只剩下一個數，所以就不用排了，現在的數組序列是下圖這個樣子：

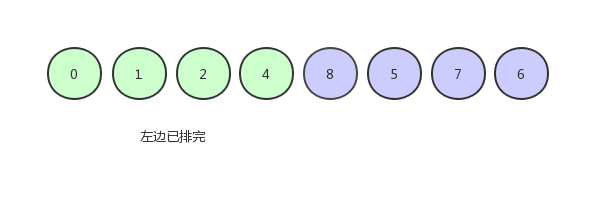
快速排序5

?右邊以同樣的操作進行，即可排序完成。

1、選取第一個數為基準

2、將比基準小的數交換到前面，比基準大的數交換到后面

3、對左右區間重復第二步，直到各區間只有一個數

void quickSort(vector<int>&numbers, int low, int high) {//  numbers = {10,8,4,6,9,10,123,6,2,14,3,8,5};if (low >= high) return;int first = low, last = high, key = numbers[low];cout << low << " " << high << " "<<key << endl;for (int i = 0; i < numbers.size(); ++i) {cout << numbers[i] << " ";}cout << endl;while (first < last) {//從后往前找比他小的放前面,從前往后找比他大的放在后面，//以第一個數為基準，必須先從后往前走，再從前往后走while (first < last && numbers[last] >= key)last--;if (first < last) numbers[first++] = numbers[last];while (first < last && numbers[first] <= key)first++;if (first < last) numbers[last--] = numbers[first];}numbers[first] = key;cout << "the index " << first << "  value " << key << endl;quickSort(numbers, low, first - 1);quickSort(numbers, first + 1, high);
}

?希爾排序

?排序過程如下圖所示：

希爾排序是插入排序的一種變種。無論是插入排序還是冒泡排序，如果數組的最大值剛好是在第一位，要將它挪到正確的位置就需要 n - 1 次移動。

也就是說，原數組的一個元素如果距離它正確的位置很遠的話，則需要與相鄰元素交換很多次才能到達正確的位置，這樣是相對比較花時間了。

希爾排序就是為了加快速度簡單地改進了插入排序，交換不相鄰的元素以對數組的局部進行排序。

希爾排序的思想是采用插入排序的方法，先讓數組中任意間隔為 h 的元素有序，剛開始 h 的大小可以是 h = n / 2,接著讓 h = n / 4，讓 h 一直縮小，當 h = 1 時，也就是此時數組中任意間隔為1的元素有序，此時的數組就是有序的了。


void shellSortCore(vector<int>& nums, int gap, int i) {int inserted = nums[i];int j;//  插入的時候按組進行插入for (j = i - gap; j >= 0 && inserted < nums[j]; j -= gap) {nums[j + gap] = nums[j];}nums[j + gap] = inserted;
}void shellSort(vector<int>& nums) {int len = nums.size();//進行分組，最開始的時候，gap為數組長度一半for (int gap = len / 2; gap > 0; gap /= 2) {//對各個分組進行插入分組for (int i = gap; i < len; ++i) {//將nums[i]插入到所在分組正確的位置上shellSortCore(nums,gap,i);}}}

歸并排序

?排序過程如下圖所示：

1、把長度為n的輸入序列分成兩個長度為n/2的子序列；

2、對這兩個子序列分別采用歸并排序；

3、將兩個排序好的子序列合并成一個最終的排序序列。

void mergeSortCore(vector<int>& data, vector<int>& dataTemp, int low, int high) {if (low >= high) return;int len = high - low, mid = low + len / 2;int start1 = low, end1 = mid, start2 = mid + 1, end2 = high;mergeSortCore(data, dataTemp, start1, end1);mergeSortCore(data, dataTemp, start2, end2);int index = low;while (start1 <= end1 && start2 <= end2) {dataTemp[index++] = data[start1] < data[start2] ? data[start1++] : data[start2++];}while (start1 <= end1) {dataTemp[index++] = data[start1++];}while (start2 <= end2) {dataTemp[index++] = data[start2++];}for (index = low; index <= high; ++index) {data[index] = dataTemp[index];}
}void mergeSort(vector<int>& data) {int len = data.size();vector<int> dataTemp(len, 0);mergeSortCore(data, dataTemp, 0, len - 1);
}

堆排序

分為創建堆和堆排序兩個部分

創建堆（這里假定是大根堆）時，要保證每個父節點的值比左右子節點的值大

當每次堆排序完成后，最頂端的即是當前堆的最大值，隨后可以將堆的最大值與堆的倒數第一個元素互換，因為此時當前最大值已經完成排序，將其趕出堆內，堆的size減1，剩下的元素進行堆重構。

堆重構的過程就是維持堆每個父節點的值大于左右子節點值的過程

#include <iostream>
#include <algorithm>
#include <vector>using namespace std;//i位置的數，向上調整大根堆
void heapInsert(vector<int>& arr, int i)
{while (arr[i] > arr[(i - 1) / 2])    //子節點比父節點大{swap(arr[i], arr[(i - 1) / 2]);i = (i - 1) / 2;}}//i位置的數發生了變化，又想維持住大根堆的結構
void heapify(vector<int>& arr, int i, int size)
{int l = 2 * i + 1;  //左孩子while (l < size){int best = l + 1 < size && arr[l + 1] > arr[l] ?  l + 1 : l;best = arr[best] > arr[i] ? best : i;if (best == i)break;swap(arr[i], arr[best]);i = best;l = 2 * i + 1;}}//從頂到底建立大根堆
//依次彈出堆內的最大值，并重新排好序
void heapSort(vector<int>& arr)
{int size = arr.size();for (int i = 0; i < size; i++)    //建立大根堆{heapInsert(arr, i);}while (size > 1){swap(arr[0], arr[size - 1]);  size--;cout<< arr[size] <<endl;heapify(arr, 0, size);}
}int main()
{vector<int> arr = { 3,2,1,5,6,4 };heapSort(arr);
}

計數排序

計數排序用于元素大小范圍有限的數值排序。

如果 k（待排數組的最大值）過大則會引起較大的空間復雜度，一般是用來排序 0 到 100 之間的數字的最好的算法，但是它不適合按字母順序排序人名。

統計小于等于該元素值的元素的個數i，于是該元素就放在目標數組的索引i位（i≥0）

計數排序

找出待排序的數組中最大和最小的元素；
統計數組中每個值為 i 的元素出現的次數，存入數組 C 的第 i 項；
對所有的計數累加（從 C 中的第一個元素開始，每一項和前一項相加）；
向填充目標數組：將每個元素 i 放在新數組的第 C[i] 項，每放一個元素就將 C[i] 減去 1

#include <iostream>
#include <vector>
#include <algorithm>using namespace std;// 計數排序
void CountSort(vector<int>& vecRaw, vector<int>& vecObj)
{// 確保待排序容器非空if (vecRaw.size() == 0)return;// 使用 vecRaw 的最大值 + 1 作為計數容器 countVec 的大小int vecCountLength = (*max_element(begin(vecRaw), end(vecRaw))) + 1;vector<int> vecCount(vecCountLength, 0);// 統計每個鍵值出現的次數for (int i = 0; i < vecRaw.size(); i++)vecCount[vecRaw[i]]++;// 后面的鍵值出現的位置為前面所有鍵值出現的次數之和for (int i = 1; i < vecCountLength; i++)vecCount[i] += vecCount[i - 1];// 將鍵值放到目標位置for (int i = vecRaw.size(); i > 0; i--)	// 此處逆序是為了保持相同鍵值的穩定性vecObj[--vecCount[vecRaw[i - 1]]] = vecRaw[i - 1];
}int main()
{vector<int> vecRaw = { 0,5,7,9,6,3,4,5,2,8,6,9,2,1 };vector<int> vecObj(vecRaw.size(), 0);CountSort(vecRaw, vecObj);for (int i = 0; i < vecObj.size(); ++i)cout << vecObj[i] << "  ";cout << endl;return 0;
}

桶排序

?排序過程如下圖所示：

桶排序

設置一個定量的數組當作空桶子。
尋訪序列，并且把項目一個一個放到對應的桶子去。
對每個不是空的桶子進行排序。
從不是空的桶子里把項目再放回原來的序列中。

#include<stdio.h>
int main() {int book[1001],i,j,t;//初始化桶數組for(i=0;i<=1000;i++) {book[i] = 0;}//輸入一個數n，表示接下來有n個數scanf("%d",&n);for(i = 1;i<=n;i++) {//把每一個數讀到變量中去scanf("%d",&t);//計數  book[t]++;}//從大到小輸出for(i = 1000;i>=0;i--) {for(j=1;j<=book[i];j++) {printf("%d",i);}}getchar();getchar();//getchar()用來暫停程序，以便查看程序輸出的內容//也可以用system("pause");來代替return 0;
}

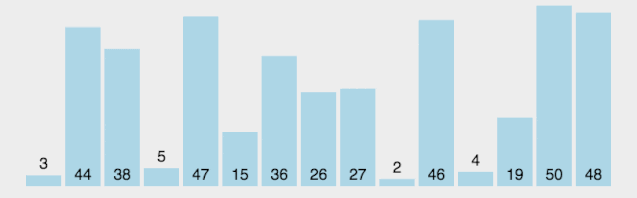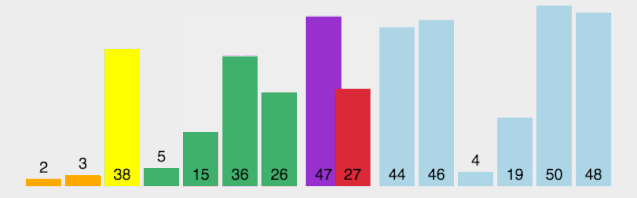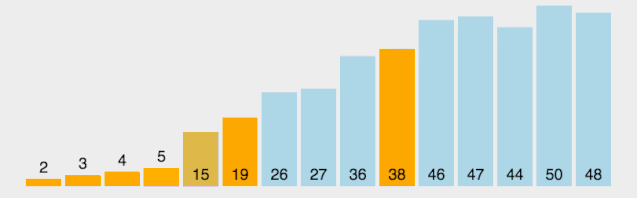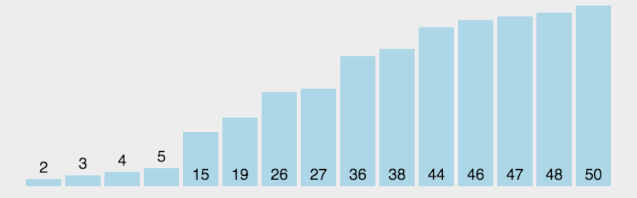
基數排序

取得數組中的最大數，并取得位數；
arr為原始數組，從最低位開始取每個位組成radix數組；
對radix進行計數排序（利用計數排序適用于小范圍數的特點）

int maxbit(int data[], int n) //輔助函數，求數據的最大位數
{int maxData = data[0];		///< 最大數/// 先求出最大數，再求其位數，這樣有原先依次每個數判斷其位數，稍微優化點。for (int i = 1; i < n; ++i){if (maxData < data[i])maxData = data[i];}int d = 1;int p = 10;while (maxData >= p){//p *= 10; // Maybe overflowmaxData /= 10;++d;}return d;
}
void radixsort(int data[], int n) //基數排序
{int d = maxbit(data, n);int *tmp = new int[n];int *count = new int[10]; //計數器int i, j, k;int radix = 1;for(i = 1; i <= d; i++) //進行d次排序{for(j = 0; j < 10; j++)count[j] = 0; //每次分配前清空計數器for(j = 0; j < n; j++){k = (data[j] / radix) % 10; //統計每個桶中的記錄數count[k]++;}for(j = 1; j < 10; j++)count[j] = count[j - 1] + count[j]; //將tmp中的位置依次分配給每個桶for(j = n - 1; j >= 0; j--) //將所有桶中記錄依次收集到tmp中{k = (data[j] / radix) % 10;tmp[count[k] - 1] = data[j];count[k]--;}for(j = 0; j < n; j++) //將臨時數組的內容復制到data中data[j] = tmp[j];radix = radix * 10;}delete []tmp;delete []count;
}