題目

輸入一個矩陣，按照從外向里以順時針的順序依次打印出每一個數字。

示例 1：

輸入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
輸出：[1,2,3,6,9,8,7,4,5]

示例 2：

輸入：matrix =?[[1,2,3,4],[5,6,7,8],[9,10,11,12]]
輸出：[1,2,3,4,8,12,11,10,9,5,6,7]

劍指 Offer 29. 順時針打印矩陣 - 力扣（LeetCode）

與 力扣54題相同

54.?螺旋矩陣

思路

二維數組順時針從外往里走

可以想象成：按照 右-》下-》左 -》上 的順序一直走，走過的地方不要走即可。

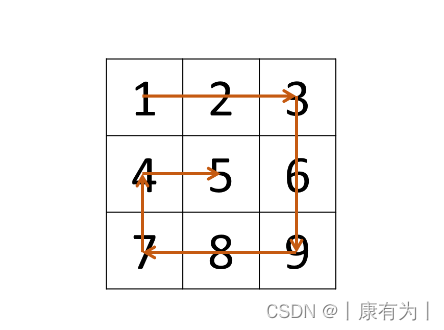
1. 每走過一個地方，就標記一下，這樣下次就不會再走這里了

2. 循環往右走，直到不能走為止（不能走：既不超出數組邊界，并且下一個地方沒有走過的標記）

3.?循環往下走，直到不能走為止

4.?循環往左走，直到不能走為止

5.?循環往上走，直到不能走為止

6. 重復2345這四步，直到四面八方沒有一個地方可以走

代碼

class Solution {public int[] spiralOrder(int[][] matrix) {int i = 0;int j = 0;int m = matrix.length;if (m == 0)return new int[0];int n = matrix[0].length;int passingFlag = Integer.MIN_VALUE;int res [] = new int[m * n];int p = 0;res[p] = matrix[i][j];matrix[i][j] = passingFlag;//上下左右有一個地方能走就行while ((j+1< n && matrix[i][j+1] != passingFlag)||  (i+1< m && matrix[i+1][j] != passingFlag) || (j - 1 >= 0 && matrix[i][j - 1] != passingFlag) || (i - 1 >= 0 && matrix[i-1][j] != passingFlag)){//往右走while (j+1< n && matrix[i][j+1] != passingFlag){j = j + 1;p++;res[p] = matrix[i][j];matrix[i][j] = passingFlag;}//往下走while (i+1< m && matrix[i+1][j] != passingFlag){i = i + 1 ;p++;res[p] = matrix[i][j];matrix[i][j] = passingFlag;}//往左走while (j - 1 >= 0 && matrix[i][j - 1] != passingFlag){j = j - 1;p++;res[p] = matrix[i][j];matrix[i][j] = passingFlag;}//往上走while (i - 1 >= 0 && matrix[i-1][j] != passingFlag){i = i - 1;p++;res[p] = matrix[i][j];matrix[i][j] = passingFlag;}}return res;}
}

效果

可以優化的地方：

1.走過標記

????????走過的標記，這里我使用的是：走過一個地方就讓那里變成最小值Integer.MIN_VALUE，但是這么做不嚴謹，因為測試例子里沒有走過最小值，所以我通過了。

????????官方的做法是：用一個輔助矩陣，也就是再做一個二維數組，走過原數組，就在輔助數組上標記一下，這么做才合情合理。

2.結束條件

? ? ? ? 判斷外層大循環結束，我的條件是只要四面八方都不能走了，就停止。

? ? ? ? 官方的結束條件是，只要結果數組滿了，就結束。

? ? ? ? 這樣看來 官方的解法要比我少判斷一些東西。

也就是將

        while ((j+1< n && matrix[i][j+1] != passingFlag)||  (i+1< m && matrix[i+1][j] != passingFlag) || (j - 1 >= 0 && matrix[i][j - 1] != passingFlag) || (i - 1 >= 0 && matrix[i-1][j] != passingFlag)){

替換成

        while (p+1 < m*n){

代碼會簡潔很多