本篇文章主要介紹了Dijkstra迪杰斯特拉算法的C++實現,文章包含兩個部分,在第一部分中我會簡單介紹迪杰斯特拉算法以及一些個人的理解,第二部分會對C++代碼的邏輯進行解釋。下面是我已經上傳的代碼資源,大家有興趣的可以點擊鏈接下載資源。
迪杰斯特拉算法的C++實現
迪杰斯特拉算法本質上是一個貪心算法,通過不斷迭代取得局部最優解的方法,最終找到整體的最優解。迪杰斯特拉算法主要用于在有權圖中計算出各節點到初始節點的最短路徑。在接下來的分析中我會使用的有權圖如下 :
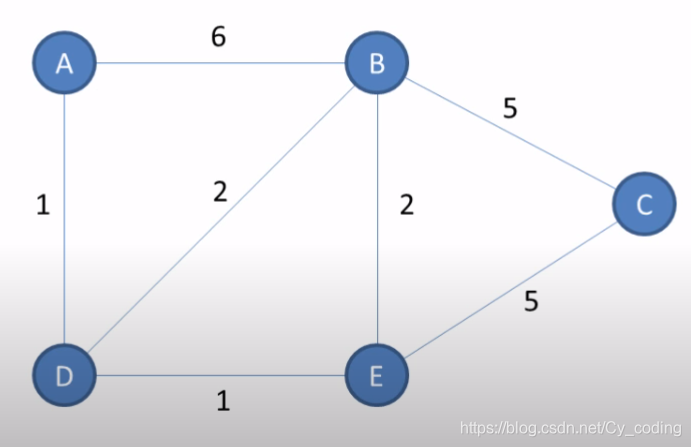
其中,ABCDE就是我們需要遍歷的節點,連接節點的弦上的數字表示了兩節點之間的"距離",或稱之為權重,消耗。需要注意的幾點是 :
- 迪杰斯特拉算法適用的有權圖中,節點之間的權重不要求是雙向的,即 A-> B的權重和 B->A 的權重不要求相同。換而言之,有權圖中節點之間的連接可以是單向的,或者在兩個方向權重有所不同的。
- 迪杰斯特拉算法適用的有權圖中,節點間連接的權重值不能是負值。
了解了迪杰斯特拉算法的一些注意點之后,我們下面來重點解釋算法的實現。之前我們已經提到了,迪杰斯特拉算法多用于解決最短路徑問題,對應上述有權圖就是計算出所有節點到初始節點的最短距離。在下述例子中,我們默認使用A作為初始節點,目標就是找出所有節點到A的最短距離以及所經過的路徑。
首先我們需要兩個列表,一個visited列表用于存放已經遍歷過其所有鄰節點的節點,一個unvisited列表用于存放還未遍歷過其所有鄰節點的節點。我們會不斷地進行迭代運算,直到unvisited列表為空,即所有的節點都已經訪問過(遍歷過其所有鄰節點)。
顯然初始狀態,visited列表為空[],unvisited列表中包含所有的節點[A,B,C,D,E]。
然后我們需要一個列表用于記錄所有節點到A節點,起始節點之間的最短距離,以及最短路徑中該節點之前的節點。
第一步,初始化這個表格 :
顯然A到A的距離為0,其余節點到A的距離為未知,初始化為正無窮。
| 節點 | 節點到A的距離 | 最短路徑中該節點之前的節點 |
|---|---|---|
| A | 0 | |
| B | ∞\infin∞ | |
| C | ∞\infin∞ | |
| D | ∞\infin∞ | |
| E | ∞\infin∞ |
那么每一次迭代,我們需要做的,就是在unvisited列表中,選擇一個到A距離最短的節點,并遍歷更新其所有unvisited列表中的鄰節點。
例如第一次迭代中,unvisited未訪問列表中A節點到A的最短距離最短,那么我們首先就訪問A所有unvisited的節點 B 和 D。簡單來說,如果通過A訪問B比起之前的方式要距離更短,那么我們就更新B到初始點的距離為新的最短距離,并將B之前的節點更新為A。那么在這個例子中,通過A訪問B的距離為6,通過A訪問D的距離為1,顯然距離都比正無窮要小,則更新列表如下 :
| 節點 | 節點到A的距離 | 最短路徑中該節點之前的節點 |
|---|---|---|
| A | 0 | |
| B | 6 | A |
| C | ∞\infin∞ | |
| D | 1 | A |
| E | ∞\infin∞ |
同時更新visited列表以及unvisited列表:
visited : [A]
unvisited : [B,C,D,E]
既然未訪問列表仍然不為空,我們繼續迭代,選擇D作為新的訪問節點,因為節點D目前到A的距離最短。那么節點D在unvisited列表中的鄰節點有 B E,那么我們更新B,E的值和其原來的距離進行對比。 B : 1+2 = 3 < 6 \space? E : 1+1 = 2 < ∞\infin∞。
更新列表如下 :
| 節點 | 節點到A的距離 | 最短路徑中該節點之前的節點 |
|---|---|---|
| 0 | ||
| B | 1+2 = 3 | D |
| C | ∞\infin∞ | |
| D | 1 | A |
| E | 1+1 = 2 | D |
同時更新visited列表以及unvisited列表:
visited : [A,D]
unvisited : [B,C,E]
我們繼續迭代,方法同上。
訪問E節點,更新列表 :
| 節點 | 節點到A的距離 | 最短路徑中該節點之前的節點 |
|---|---|---|
| 0 | ||
| B | 1+2 = 3 | D |
| C | 1+1+5 = 7 | E |
| 1 | A | |
| E | 1+1 = 2 | D |
同時更新visited列表以及unvisited列表:
visited : [A,D,E]
unvisited : [B,C]
繼續訪問B,更新列表 :
B的唯一沒有訪問的鄰節點為C,但A> … >B>C 的距離為 3+5=8 >7,因此C到節點A的距離不變。
| 節點 | 節點到A的距離 | 最短路徑中該節點之前的節點 |
|---|---|---|
| 0 | ||
| B | 1+2 = 3 | D |
| C | 1+1+5 = 7 | E |
| 1 | A | |
| 1+1 = 2 | D |
同時更新visited列表以及unvisited列表:
visited : [A,D,E,B]
unvisited : [C]
最后我們訪問C,列表不變,因為C的所有鄰節點都已經訪問過了。
最終的結果如下 :
| 節點 | 節點到A的距離 | 最短路徑中該節點之前的節點 |
|---|---|---|
| A | 0 | |
| B | 3 | D |
| C | 7 | E |
| D | 1 | A |
| E | 2 | D |
通過迪杰斯特拉算法,我們可以完備地遍歷所有有權圖中的節點,并在最后返回一個所有節點到初始點的最短距離,以及對應的最短路徑的所有節點之前的節點。之后通過不斷訪問最短路徑中該節點之前的節點,我們就可以很簡單地還原出最短路徑。例如對節點C而言,C之前的節點為E,E之前的節點為D,D之前的節點為A,因此最短路徑還原為A > D > E > C。
參考 :
[1] Graph Data Structure 4. Dijkstra’s Shortest Path Algorithm
[2] (熟肉)Dijkstra算法詳解,輕松入門——Youtube









![[十二省聯考2019]皮配](http://pic.xiahunao.cn/[十二省聯考2019]皮配)









