機器學習的理論部分學習知識點比較亂且雜。我這里通過幾篇文章，簡單總結一下自己對機器學習理論的理解，以防遺忘。第一篇文章主要概述了機器學習的基本任務以及一個常用的降維方法，主成分分析。

機器學習的基本任務

機器學習能實現許多不同的任務，基本分為以下幾類:

1. 分類 : 算法需要判斷輸入屬于哪一種類別。例如通過一張人像圖片判斷人的身份。
2. 回歸 : 算法需要將一個數值與輸入聯系起來。例如通過氣象學的
   參數判斷24小時的溫度。
3. 重寫 : 通過觀察輸入，將其重寫為文字形式。例如通過一張谷歌街道的圖片，識別街道的名稱。
4. 翻譯 : 將一系列的符號文字轉化為另一種語言的符號和文字。例如將英語翻譯成中文，將Java代碼翻譯為對應的C++代碼。
5. 異常尋找: 判斷輸入是不是非典型的。例如檢測是否有逆行的車輛。
6. 合成 : 生成與樣本數據類似的新的樣本。例如合成另一個角度的風景圖。
7. 降噪 : 對樣本數據進行降噪處理。

協方差矩陣

協方差矩陣用于描述各個維度之間的聯系，其元素是各個向量元素之間的協方差。
例如如果我們我們有N個維度為n的向量數據$x_i$，他們的協方差矩陣如下
$$\Sigma =\frac{1}{N}\sum _{i=1}^N(x_i?\mu )(x_i?\mu {)}^T$$
其中$\mu$是數據$x_i$的平均向量。協方差矩陣維度為n*n且對稱。協方差矩陣中編碼了數據各個維度之間的相互關系，以及各個維度的方差。例如在n=2，二維平面中，協方差矩陣可以表示為 :
$$\Sigma =\left(\begin{array}{c}{\sigma }_{xx}{\sigma }_{xy}\\ {\sigma }_{yx}{\sigma }_{yy}\end{array}\right)$$
主對角線描述了該維度上數據的方差，副對角線描述了各個維度之間的協方差，當各個維度處于相同數量級時可以一定程度上反應各個維度之間的相關性。

主成分分析

現實生活中的樣本數據的分布可能與很多的潛在因素有關，因此使得我們的數據往往呈現出高維的形式。高維度的數據會對我們進行數據分析造成很多干擾，例如在我們進行分類分析時，隨著樣本容量的不斷增大，維度越高，計算量將呈幾何倍數的增長且難以避免的會有噪聲的影響。因此如何降維也是數據預處理十分重要的步驟。其中，主成分分析可以有效地降低樣本數據的維度，減少計算量的同時使得樣本數據對噪音干擾更不敏感。

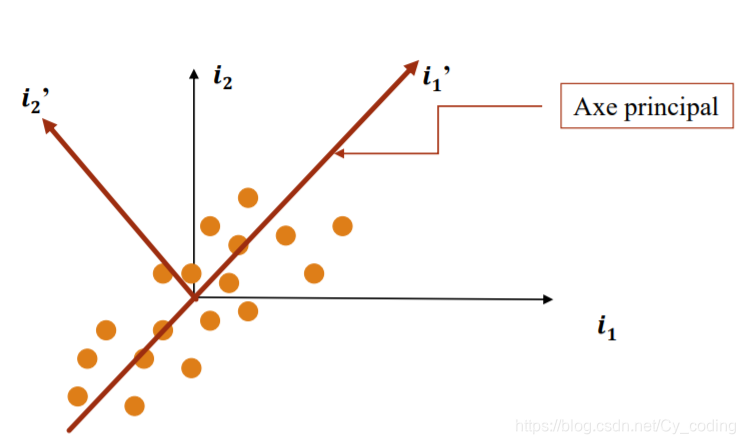
主成分分析 principal component analysis, 其中心思想是將高維度的數據，投影到低維度，以此來實現降維。例如下圖中，將原本的二維空間(O,$i_1$,$i_2$)中的數據，投影到向量$i{{}_1}^{\prime }$上。主成分分析的要點，即是將數據投影到新的坐標系中，其中坐標系的前幾個基底向量應該包含樣本數據最多的信息量。在進行主成分分析之間，要對數據進行預處理，中心化規格化數據，即對每個數據作減去平均值并除以標準差的操作。

主成分分析的數學表示如下:
對于每個在原始坐標系中的數據點$x_i$,$x_i=x_{i1}{i}_1+x_{i2}{i}_1+...+x_{in}{i}_1$，其中$x_{in}$是$x_i$在各個維度的分量。將數據投影到新的坐標軸$i{{}_1}^{\prime }$后，新的坐標為$x{{}_{i1}}^{\prime }=x{{}_i}^{T}i{{}_1}^{\prime }$。數據集沿著新的坐標軸$i{{}_1}^{\prime }$的方差計算如下:
$$\sigma =\frac{1}{N}\sum _{i=1}^{N}x{{}_{i1}}^{\prime 2}=\frac{1}{N}\sum _{i=1}^{N}x{{}_{i1}}^{\prime T}x{{}_{i1}}^{\prime }=\frac{1}{N}\sum _{i=1}^{N}i{{}_1}^{\prime T}{x}_i{x}_i^{T}i{{}_1}^{\prime }$$

$$=\frac{1}{N}i{{}_1}^{\prime T}(\sum _{i=1}^N{x}_i{x}_i^T)i{{}_1}^{\prime }$$
$$\sigma =i{{}_1}^{\prime T}\Sigma i{{}_1}^{\prime }$$
其中 $\Sigma$ 是協方差矩陣 $$\Sigma =\frac{1}{N}(\sum _{i=1}^N{x}_i{x}_i^T)$$
在進行主成分分析時，我們假設某一維度所包含的信息量，與該維度數據的方差是呈正相關的，因此主成分分析問題就轉化成了最大值問題，使用拉格朗日乘數法，找到使方差最大化的剩余維度:
$$L=i{{}_1}^{\prime T}\Sigma i_1?\lambda (i{{}_1}^{\prime T}i{{}_1}^{\prime }?1)$$
$$\frac{?L}{?i{{}_1}^{\prime }}=0即\Sigma i{{}_1}^{\prime }=\lambda {i_1}^{\prime }$$

其中，$i{{}_1}^{\prime }$ 和 $\lambda$ 分別是數據協方差矩陣的特征向量和對應的特征值。第一個投影維度對應協方差矩陣的第一個特征向量(特征值最大的特征向量)。第二個投影維度對應第二個特征向量以此類推，我們可以得到一組對應特征值遞減的特征向量。通過選出協方差矩陣的前K個特征向量，我們就能選出包含信息量最大的主成分維度，實現對原始數據的降噪，排除掉高維度的干擾，使得后續的數據分析成果更穩定。

Tips : 協方差矩陣是對稱構成的且至少是半正定矩陣，因此其所有的特征向量都是實數，所有的特征值都是正數或0，所有的特征向量互相垂直不相關。