Hidden Markov Model, HMM 隱馬爾可夫模型，是一種描述隱性變量(狀態)和顯性變量(觀測狀態)之間關系的模型。該模型遵循兩個假設，隱性狀態i只取決于前一個隱性狀態i-1，而與其他先前的隱形狀態無關。觀測狀態也只取決于當前的隱形狀態。因此我們常常將隱馬爾科夫模型表現為一種如下圖所示鏈式的模型。

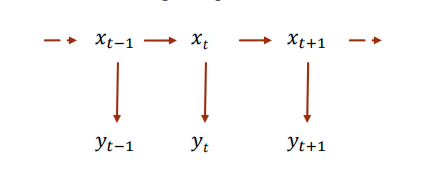
其中，$x_t$代表某一時刻的隱形狀態鏈，其N個狀態取值集合為{s1,s2,s3,...,N}\{s_1,s_2,s_3,...,_N\}{s1?,s2?,s3?,...,N?}。$y_t$表示為對應的該時刻的顯性狀態(觀測狀態)，其M個狀態取值集合為{o1,o2,o3,...,ok,...,oM}\{o_1,o_2,o_3,...,o_k,...,o_M\}{o1?,o2?,o3?,...,ok?,...,oM?}。隱馬爾科夫模型$\theta$可以由三個矩陣來進行描述$\theta =(A,B,\Pi )$。

1. 大小為 N*N (N代表N種隱性的狀態)的過渡矩陣 A:

A={aij}={P(xt+1=sj∣xt=si)}={P(sj∣si)}A = \{a_{ij}\} = \{P(x_{t+1}=s_j|x_t=s_i)\} = \{P(s_j|s_i)\}A={aij?}={P(xt+1?=sj?∣xt?=si?)}={P(sj?∣si?)}
過渡矩陣A中的每一個元素表示由上一個隱性狀態$s_i$變為下一個隱性狀態的條件概率。

2. 大小為 1*N 的初始概率向量 $\Pi$ :

$$\Pi ={\pi }_i=P(x_1=s_i)=P(s_i)$$
初始概率向量$\Pi$中的每一個元素，表示初始隱性狀態為$s_i$的概率，該向量的長度N與隱性狀態的可能取值個數相同。

3. 大小為 M*N 的觀測矩陣 B :

B={bki}={P(yt=ok∣xt=si)}={P(ok∣si)}B = \{b_{ki}\} = \{P(y_t=o_k|x_t=s_i)\} = \{P(o_k|s_i)\} B={bki?}={P(yt?=ok?∣xt?=si?)}={P(ok?∣si?)}

觀測矩陣B中的每個元素，是用來描述N個隱形狀態對應M個觀測狀態的概率。即在隱形狀態為$s_i$ 的條件下，觀測狀態為$o_k$的概率。

上述三個矩陣構成了一個完整的隱馬爾可夫模型。

擲骰子問題可以幫助我們更好地理解顯性狀態鏈和隱性狀態鏈。例如我們有三個面數不一樣的骰子可供選擇投擲，三個骰子一個面數為4，一個面數為6，一個面數為8。每次選擇的骰子是隨機的且滿足繼續選到同一個骰子的概率是選到其他骰子概率的兩倍。此時，隱性狀態鏈$x_t$就是我們每次選擇的骰子，取值集合就是骰子1，骰子2，骰子3。顯性狀態鏈就是我們擲出的一系列數值，取值集合為{1,2,3,4,5,6,7,8}\{1,2,3,4,5,6,7,8\}{1,2,3,4,5,6,7,8}。
根據上述的信息，我們不難整理出這個骰子問題HMM模型的三個核心矩陣 :

過渡矩陣A

previous state \ current state	D4	D6	D8
D4	$\frac{2}{3}$	$\frac{1}{6}$	$\frac{1}{6}$
D6	$\frac{1}{6}$	$\frac{2}{3}$	$\frac{1}{6}$
D8	$\frac{1}{6}$	$\frac{1}{6}$	$\frac{2}{3}$

初始概率向量$\Pi$
由于一開始是隨機選取骰子，因此初始抽到三個骰子的概率是相同的$\frac{1}{3}$。

D4	D6	D8
$\frac{1}{3}$	$\frac{1}{3}$	$\frac{1}{3}$

觀測矩陣B :
觀測矩陣存放了每種隱性狀態下各觀測狀態的條件概率

observed state \ hidden state	D4	D6	D8
1	$\frac{1}{4}$	$\frac{1}{6}$	$\frac{1}{8}$
2	$\frac{1}{4}$	$\frac{1}{6}$	$\frac{1}{8}$
3	$\frac{1}{4}$	$\frac{1}{6}$	$\frac{1}{8}$
4	$\frac{1}{4}$	$\frac{1}{6}$	$\frac{1}{8}$
5	0	$\frac{1}{6}$	$\frac{1}{8}$
6	0	$\frac{1}{6}$	$\frac{1}{8}$
7	0	0	$\frac{1}{8}$
8	0	0	$\frac{1}{8}$

使用HMM模型會衍生出三類基礎問題 :

第一類問題. 在HMM模型$\theta$確定的情況下，針對一組顯性狀態鏈$y_{1:T}$，計算出該模型生成這組顯性狀態鏈的概率。

還是沿用上述的骰子為例，這類問題實際就是在確定了骰子的種類，D4D6D8(觀測矩陣B)，隨機選擇骰子的方式(過渡矩陣A和初始概率向量$\Pi$)的情況下，用于計算使用這三個骰子擲出一組數的可能性的問題。計算顯性狀態鏈的生成概率也是對模型是否和實際情況吻合的檢驗。如果多次實驗得出的顯性狀態鏈由該模型生成的概率很低，可以認為構成模型的三個矩陣要素可能與實際情況不符，即在該例子中使用的骰子有被掉包的可能或實際隨機選取骰子的方式與模型不一致。下面給出計算該問題的其中一個算法 forward algorithm 前向算法，與之對應的還有backward algorithm 后向算法，由于兩者的思路很相似，本文中不再對backward algorithm作過多闡述。

forward algorithm 前向算法

計算一組顯性狀態鏈 $y_1,y_2,y_3,...,y_T$ (下文中統一稱$y_{1:T}$)生成的概率，即計算 𝔏 = $P(y_{1:T})$。我們先定義 ${\alpha }_i(t)=P(y_{1:t},x_t=s_i)$, 其中$s_i$是該顯性狀態鏈最后一個值對應的隱性狀態，$t$是這個顯性狀態鏈的總長度。 ${\alpha }_i(t)$即是擲出該顯性狀態鏈，且最后一個隱形狀態為$s_i$的概率，則最終要求的生成概率 𝔏 = $$\begin{gathered} P(y_{1:T})=P(y_{1:T},x_t=s_1)+P(y_{1:T},x_t=s_2)+...+P(y_{1:T},x_t=s_N) \\ =\sum _{i=1}^N{\alpha }_i(T) \end{gathered}$$
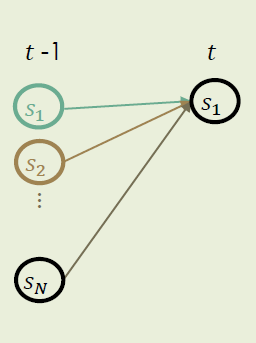
這樣我們就把問題轉化為了計算${\alpha }_i(T)=P(y_{1:T},x_t=s_i)$。使用前向算法forward algorithm如下圖所示，通過去掉最后一個狀態的狀態鏈的生成概率${\alpha }_i(t?1)$推導至${\alpha }_i(t)$，可以歸納為一個遞推模型。
首先我們計算生成$y_{1:t}$這個顯性狀態鏈且最后一個隱形狀態為$s_1$的概率${\alpha }_1(t)$，通過這個概率我們就不難推導出同樣生成該顯性狀態鏈，且最后一個隱性狀態為$s_2,s_3,...,s_N$的概率${\alpha }_i(t)$。

$$\begin{gathered} {\alpha }_1(t)=P(y_{1:t},x_t=s_i)=P(y_{1:t?1},x_{t?1}=s_1)?P(s_1|s_1)?P(y_t|s_1) \\ +P(y_{1:t?1},x_{t?1}=s_2)?P(s_1|s_2)?P(y_t|s_1) \\ + \\ ... \\ +P(y_{1:t?1},x_{t?1}=x_N)?P(s_1|s_N)?P(y_t|s_1) \end{gathered}$$

對于每個前置狀態$x_{t?1}$,計算${\alpha }_1(t)$為三個概率的乘積 : 前一時刻$t?1$隱形狀態為$s_i$且狀態鏈為$y_{1:t?1}$的概率，由前一時刻的隱形狀態$s_i$過渡到當前時刻$s_1$的過渡概率，以及在隱性狀態為$s_1$的情況下，顯性狀態呈現$y_t$的概率。
整理可得 :
$$\begin{gathered} {\alpha }_1(t)={\alpha }_1(t?1)?a_{11}?b_{yt,1} \\ + \\ {\alpha }_2(t?1)?a_{21}?b_{yt,1} \\ + \\ ... \\ + \\ {\alpha }_N(t?1)?a_{N1}?b_{yt,1} \\ =b_{yt,1}\sum _{k=1}^N{\alpha }_k(t?1)?a_{k1} \end{gathered}$$
tips : $a_{ij}$是過渡矩陣A中第i行第j列元素，$a_{ij}=P(x_{t?1}=s_j|x_t=s_i)$即由前一個隱形狀態$s_i$過渡到現狀態$s_j$的概率。

同理可得$${\alpha }_2(t)=b_{yt,2}\sum _{k=1}^N{\alpha }_k(t?1)?a_{k2}$$
不難推出$${\alpha }_i(t)=b_{yt,i}\sum _{k=1}^N{\alpha }_k(t?1)?a_{ki}for(t>=2)$$
我們就得到了一個計算${\alpha }_i(t)$的遞推模型，初始值$${\alpha }_i(1)={\pi }_i?b_{y_1,i}$$ tips : ${\pi }_i$是初始隱性狀態為i的概率(見初始概率向量$\Pi$)。

且𝔏 = $$\begin{gathered} P(y_{1:T})=P(y_{1:T},x_t=s_1)+P(y_{1:T},x_t=s_2)+...+P(y_{1:T},x_t=s_N) \\ =\sum _{i=1}^N{\alpha }_i(T) \end{gathered}$$易得$$P(y_{1:T})=\sum _{i=1}^N(b_{y_{T,1}}\sum _{k=1}^N{\alpha }_k(T?1)?a_{k1})for(T>=2)$$

第二類問題. 在HMM模型$\theta$確定的情況下，給出一組顯性狀態鏈$y_{1:T}$，找出與其對應的可能性最大 的隱性狀態序列$x_{1:T}$。

這個問題廣泛應用于自然語言處理NLP中。例如在我們獲取了一組手寫符號時，找出其最大概率對應的字符。解決這個問題我們就要用到viterbi algorithm 維特比算法。維特比算法仍然利用遞推關系,由$t$時刻的狀態推出$t+1$時刻的狀態。定義${\delta }_i(t)$為$t$時刻且顯性狀態為$s_i$的最優路徑的概率。
初始情況非常簡單，在$t=1$時刻，${\delta }_i(t)={\pi }_i?b_{y_1,i}$，每個隱性狀態對應的概率均是初始狀態概率與對應的顯性狀態觀測概率的乘積。緊接著有遞推關系 :
$${\delta }_i(t+1)=[\underset{j}{\max }{\delta }_j(t)a_{ji}]?b_{y_{t+1},i}$$在這個遞推關系中，下一時刻$t+1$每個隱性狀態$i$的最大概率${\delta }_i(t+1)$總是對應上一時刻$t$中最優路徑概率${\delta }_j(t)$與過渡概率$a_{ji}$乘積最大的隱性狀態$j$。因此，最優的隱性狀態路徑序列$\Psi_i(t) = [\argmax_j\delta_i(t)a_{ji}]。下面引用索邦大學課件上的例題作為使用維特比算法的例子 :

給定一個HMM模型$\theta$，其中
$$A=\left|\begin{array}{ccc}0.3& 0.5& 0.2\\ 0& 0.3& 0.7\\ 0& 0& 1\end{array}\right|$$

$$\Pi =\left|\begin{array}{c}0.6\\ 0.4\\ 0\end{array}\right|$$

$$B=\left|\begin{array}{ccc}1& 0.5& 0\\ 0& 0.5& 1\end{array}\right|$$
計算顯性序列為 y = [1,1,2,2] 時，對應可能性最大的隱性序列。
結果如下 :
最終的最大概率隱性狀態鏈為[1 2 3 3]，對應的概率為0.105。

第三類問題. Baum-Welch算法，給定一個序列$y_{1:T}$，估算出能最大化該序列生成概率的HMM模型的參數。

這類問題是非常常見的，HMM建模的問題。通過一組給定的顯性狀態鏈，推測出可能性最大的HMM模型。 首先我們需要用到前向算法中提到的${\alpha }_i(t)$以及后向算法中的${\beta }_i(t)$。前向算法的推導過程可以參考之前的部分，類似的后向算法如果有興趣可以自行再查找資料，這里不過多贅述只列出使用的公式。
根據之前前向算法部分，我們定義了${\alpha }_i(t)=P(y_{1:t},x_t=s_i)$這個可以遞推出的概率，${\alpha }_i(t)$代表了觀測狀態為$y_{1:t}$且第$t$個隱性狀態$s_i$的概率。同樣在后向算法中我們定義了${\beta }_i(t)=P(y_{t+1},...,y_T,x_t=s_i)$代表了觀測狀態為$y_{t+1:T}$且第$t$個隱性狀態為$s_i$的概率。

顯然我們有${\alpha }_i(t){\beta }_i(t)=P(y_{1:T},x_t=s_i)$ 且 𝔏 = $P(y_{1:T})$。

根據貝葉斯公式$P(A|B)=\frac{P(A,B)}{P(B)}$, [2] 我們不難得出在給定觀測序列$y_{1:T}$以及HMM模型$\theta$的情況下，在$t$時刻狀態是$s_i$的概率 :

$${\gamma }_i(t)=P(x_t=s_i|y_{1:T})=\frac{P(x_t=s_i,y_{1:T})}{P(y_{1:T})}=\frac{{\alpha }_i(t){\beta }_i(t)}{{\sum }_{j=1}^N{\alpha }_j(t){\beta }_j(t)}$$

在$t$時刻狀態是$s_i$，在$t+1$時刻狀態時$s_j$的概率 :
$${\xi }_{ij}=P(x_t=s_i,x_{t+1}=s_j|y_{1:T})=\frac{P(s_j|s_i){\alpha }_i(t){\beta }_j(t+1)P(y_{t+1}|s_j)}{P(y_{1:T})}=\frac{a_{ij}{\beta }_j(t+1)b_{y_{t+1},j}}{P(y_{1:T})}$$

通過這些基礎的概率，我們更新$\theta$中的參數。

初始狀態是$s_i$的概率向量:
$${\Pi }_i^{?}={\gamma }_i(1)$$

更新過渡矩陣:
$$a_{ij}^{?}=P(s_j|s_i)=\frac{{\sum }_{t=1}^{T?1}{\xi }_{ij}(t)}{{\sum }_{t=1}^{T?1}{\gamma }_i(t)}$$

更新觀測矩陣:
$$b_{o_k,i}^{?}=\frac{{\sum }_{t=1}^T{\alpha }_i(t)P(y_t|s_i)1_{y_t=o_k}}{{\sum }_{t=1}^T{\alpha }_i(t){\beta }_i(t)}$$
其中
$1_{y_t=o_k}=1when{y}_t=o_k$
$1_{y_t=o_k}=0whenelse$

不斷重復上述更新操作直至收斂，就得到了新的HMM模型。

\newline
\newline
\newline
\newline
\newline

References :

[1] Viterbi AJ (April 1967). “Error bounds for convolutional codes and an asymptotically optimum decoding algorithm”. IEEE Transactions on Information Theory. 13

[2] Baum-Welch algorithm