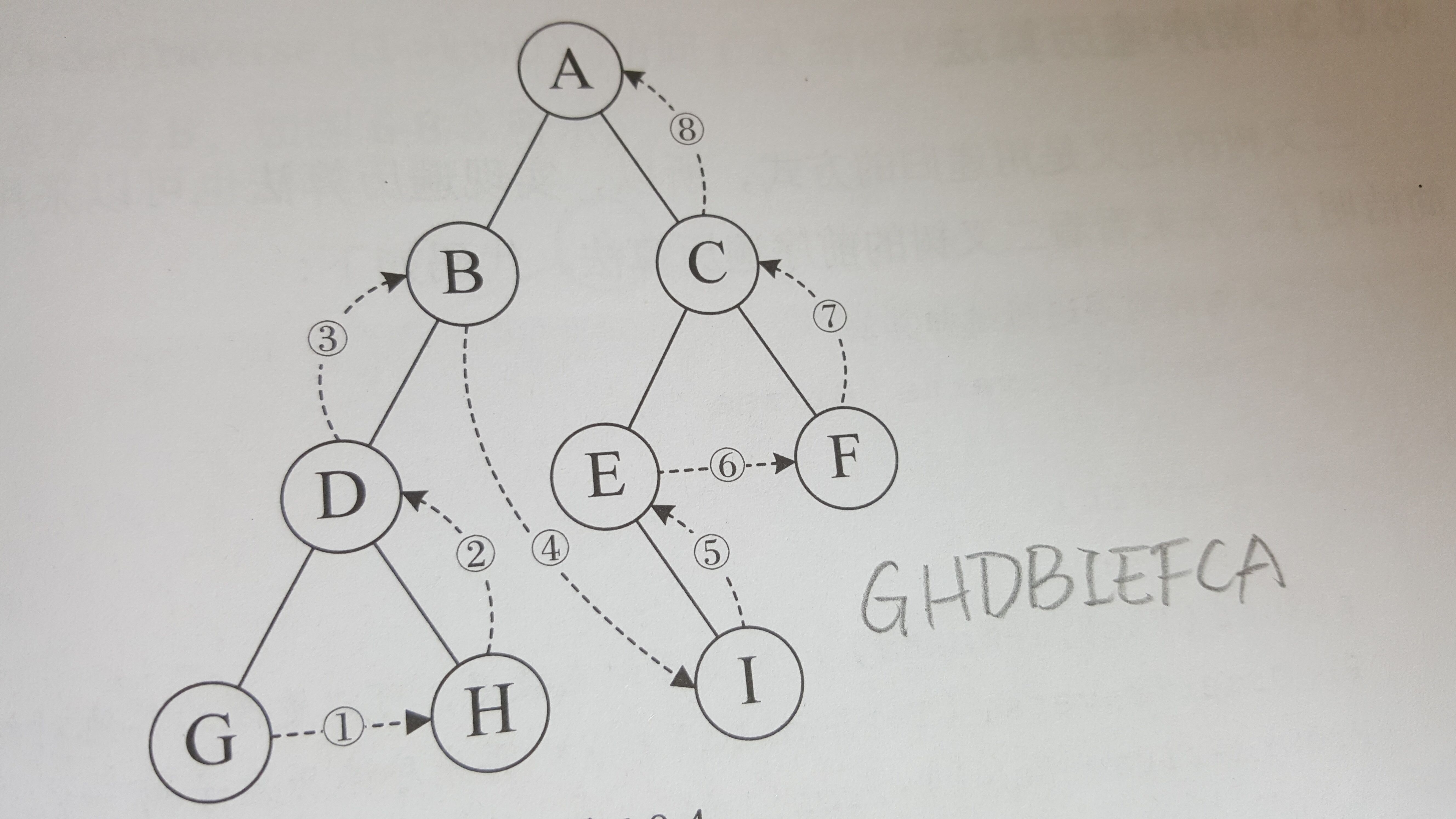
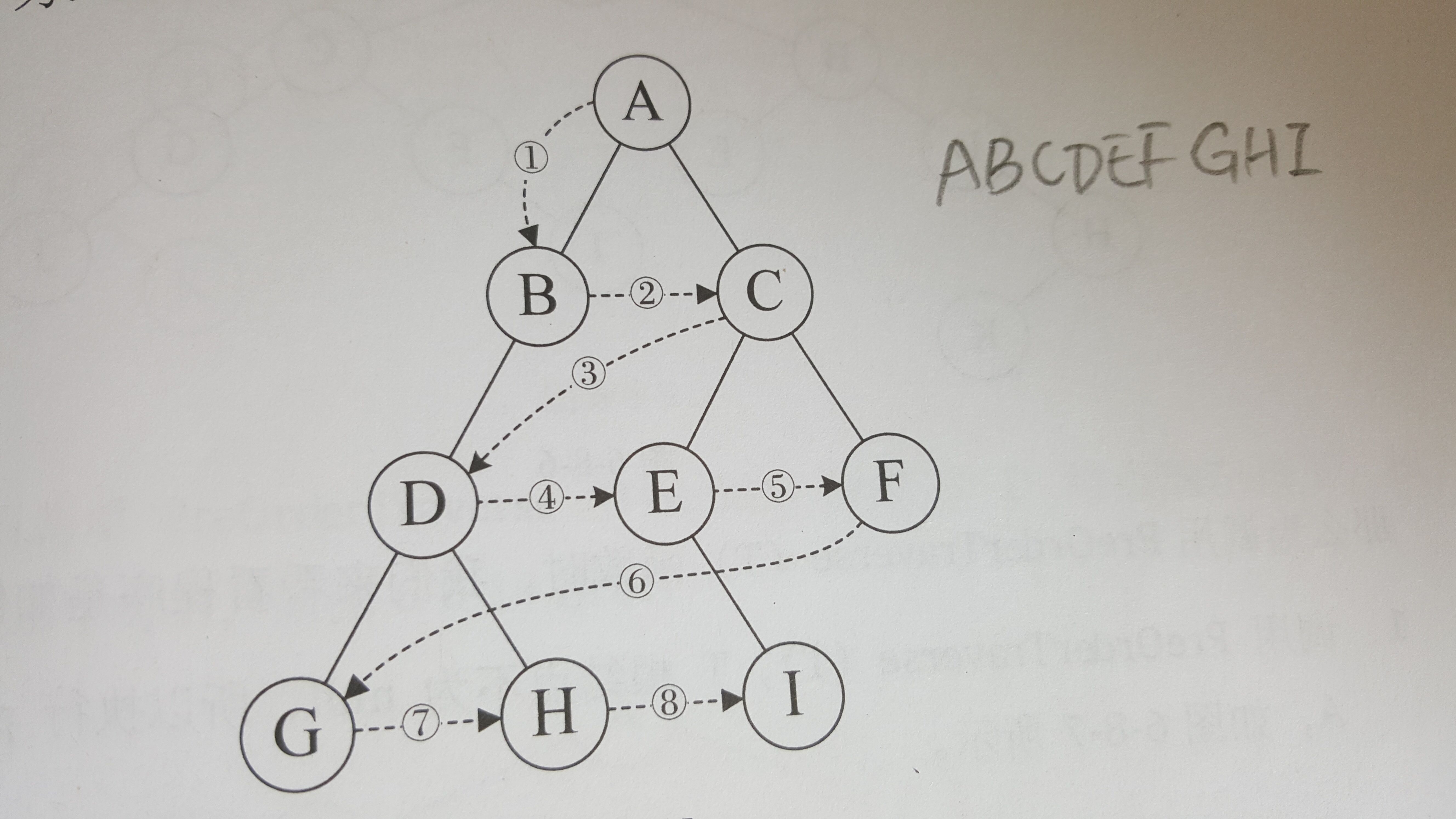
一、樹的定義
樹(Tree)是n(n>=0)個結點的有限集。 n=0又稱為空樹。在任意一課非空的樹中:(1)有且僅有一個特定的稱為跟(Root)的結點;(2)當n>1時,其余結點可分為m(m>0)個互不相交的有限集,其中每一個集合本身又是一棵樹,并且稱為根的子樹(SubTree)。
樹是一種一對多的數據結構。
需要注意的是:
(1)當n>0時根結點是惟一的,不可能存在多個根結點。
(2)m>0時,子樹的個數沒有限制,但它們一定是互不相交的。如果相交,就不符合樹的定義。
結點分類
結點擁有的子樹稱為結點的度。度為0的結點稱為葉結點或終端結點;度不為0的結點稱為非終端結點或分支結點。除根結點外,分支結點也稱為內部結點。樹的度是樹內各結點的度的最大值。如圖所示,樹的最大結點是D的度,為3,則樹的度也為3.
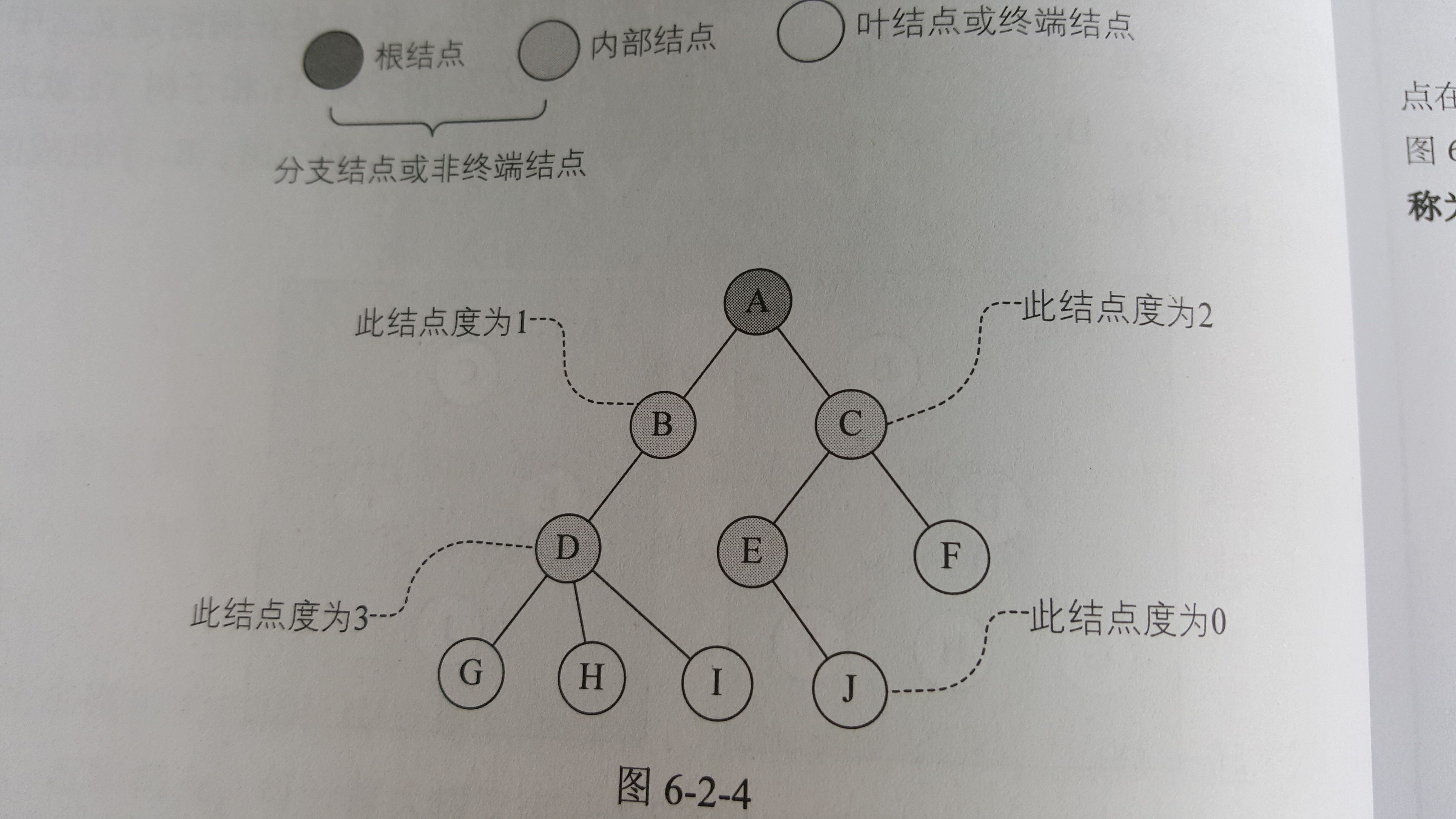
樹中結點最大的層次稱為樹的深度或高度。
如果將樹中結點的各子樹看成從左到右是有次序的,不能互換的,則稱該樹為有序樹,否則稱為無序樹。
森林是m(m>=0)棵互不相交的樹的集合。
二、樹的存儲結構
簡單的順序存儲結構和鏈式存儲結構表示不了樹一對多的關系。試想,數據元素挨個的存儲,誰是誰的雙親,誰是誰的孩子呢?
樹有自己的三種不同表示法:雙親表示法、孩子表示法、孩子兄弟表示法。
1. 雙親表示法
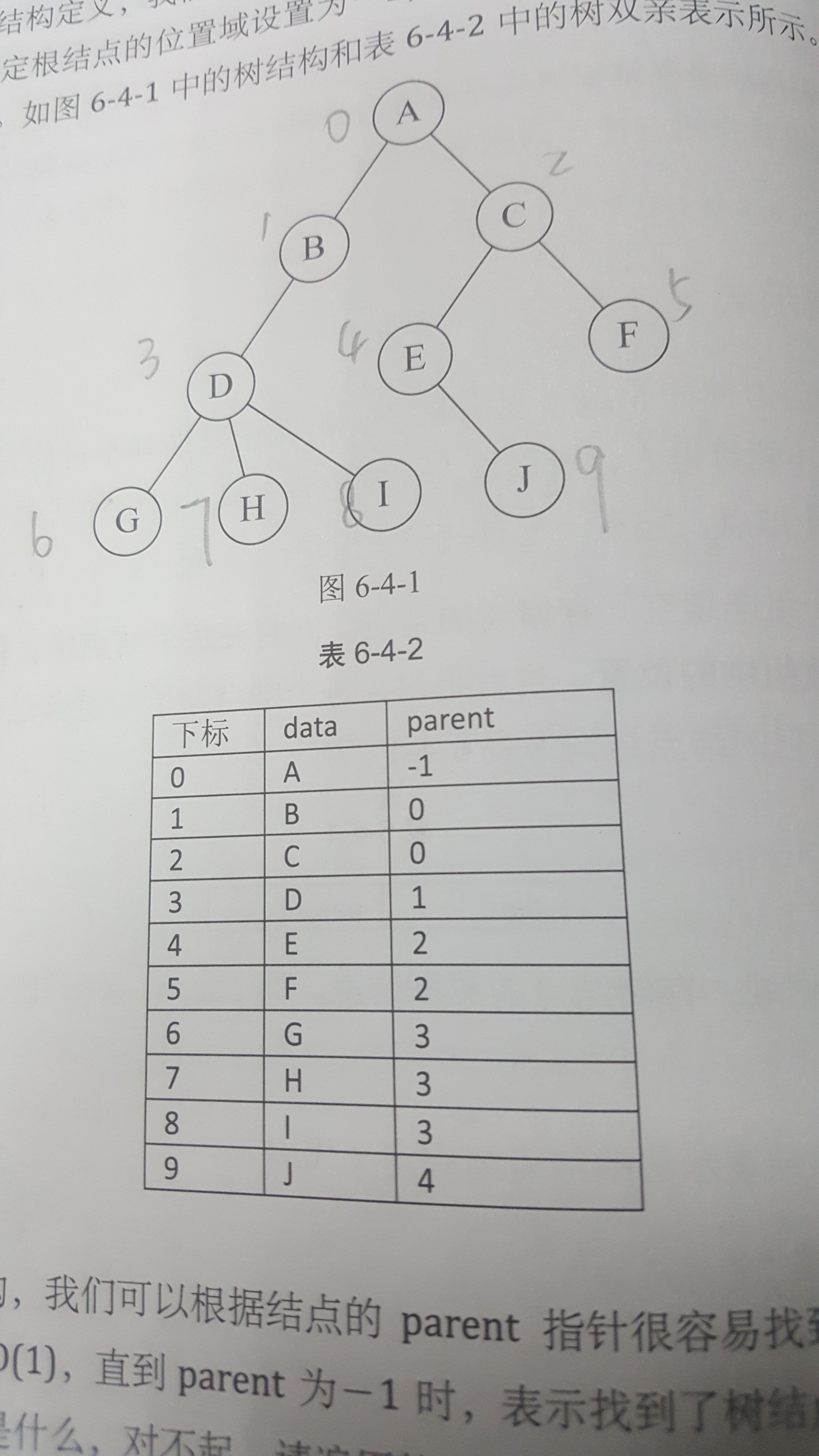
在每個結點中,附設一個指示器指示雙親結點在數組中的位置。結點結構表如下。
| data | parent |
|---|
其中,data是數據域,存儲結點的數據信息。而parent是指針域,存儲該結點的雙親在數組的下標。
標出雙親,左右結點則構成樹。
2. 孩子表示法
先介紹一種多種鏈表表示法:每個結點有多個指針域,其中每個指針指向一棵子樹的根結點。
方案一:
指針域的個數就等于樹的度。
| data | child1 | child2 | child3 | …… | childd |
|---|
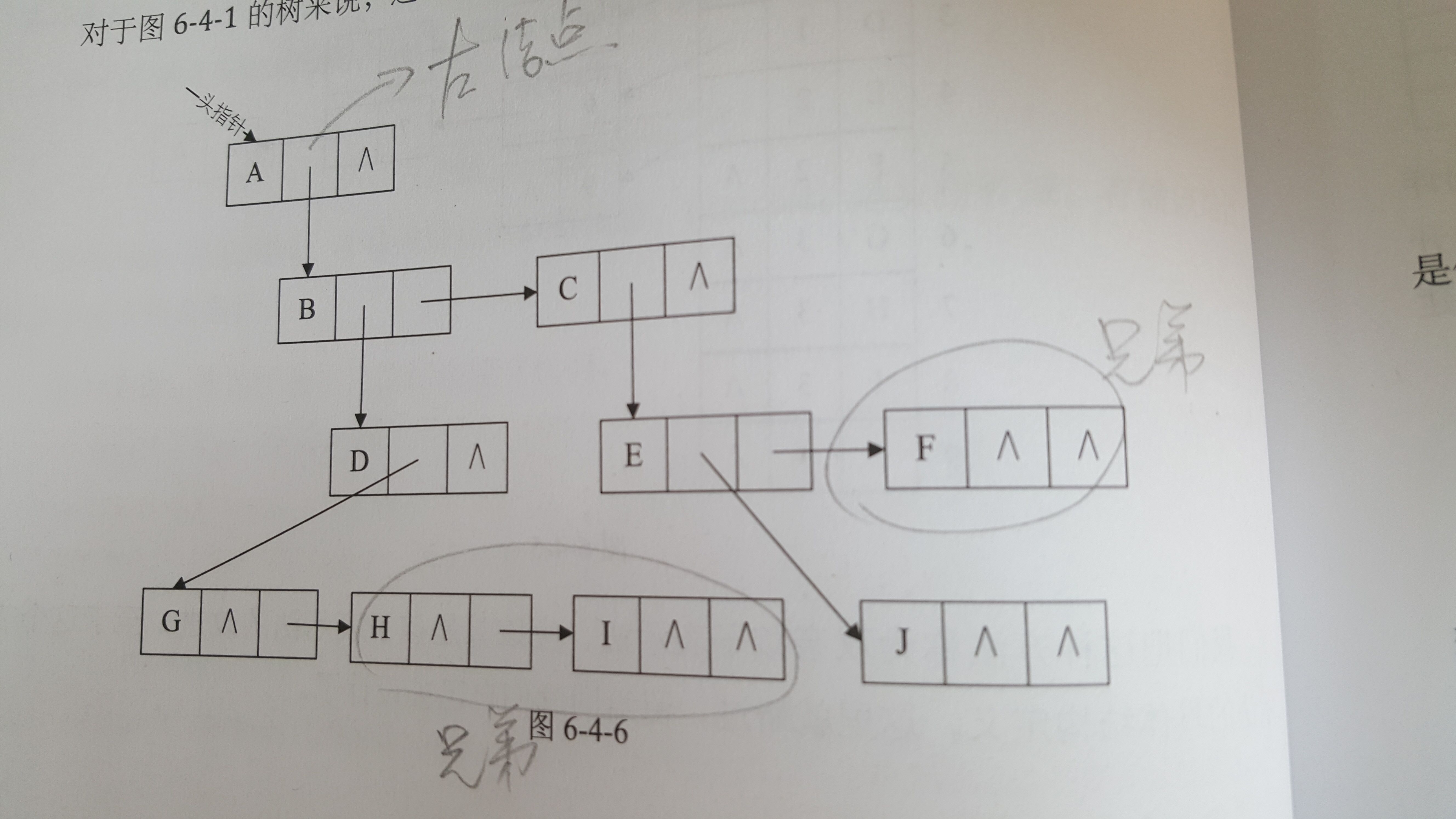
其中data是數據域,child1到childd是指針域,用來指向該結點的孩子結點。對于圖6-4-1的樹來說,樹的度是3,所以指針域的個數是3。如下圖。
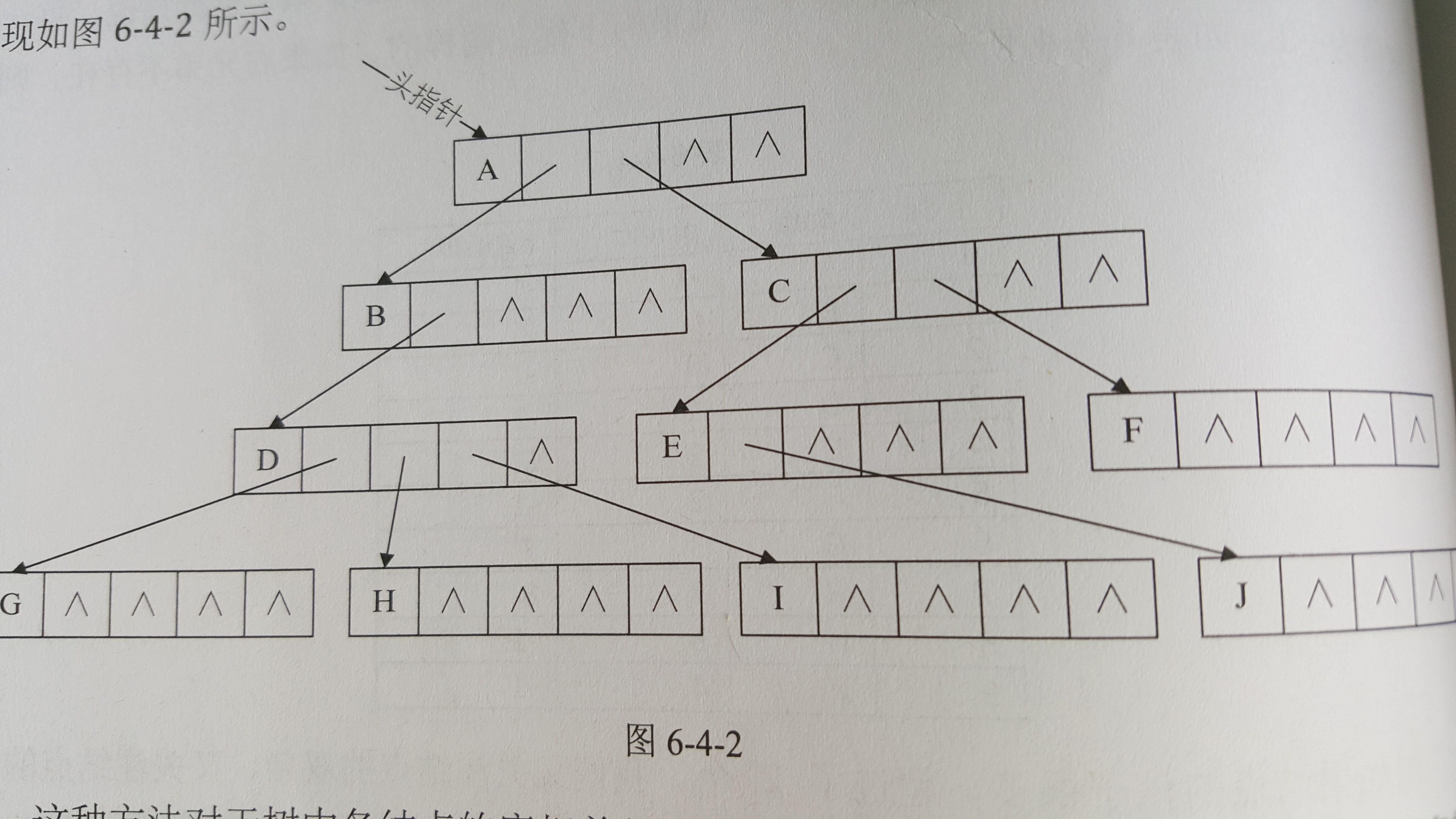
這種方法對于樹中各結點的度相差很大是,顯然是浪費空間的,因為有很多的結點,它的指針域都是空的。不過如果樹的各結點度相差很小時,那就意味著開辟的空間被充分利用了,這時存儲結構的缺點反而變成了優點。
為了按需分配空間,我們考慮方案二。
方案二:
每個結點指針域的個數等于該結點的度。
| data | degree | child2 | child2 | …… | childd |
|---|
其中data是數據域,degree為度域,也就是存儲該結點的孩子結點的個數,child1到childd為指針域,指向該結點的各孩子結點。如下圖。
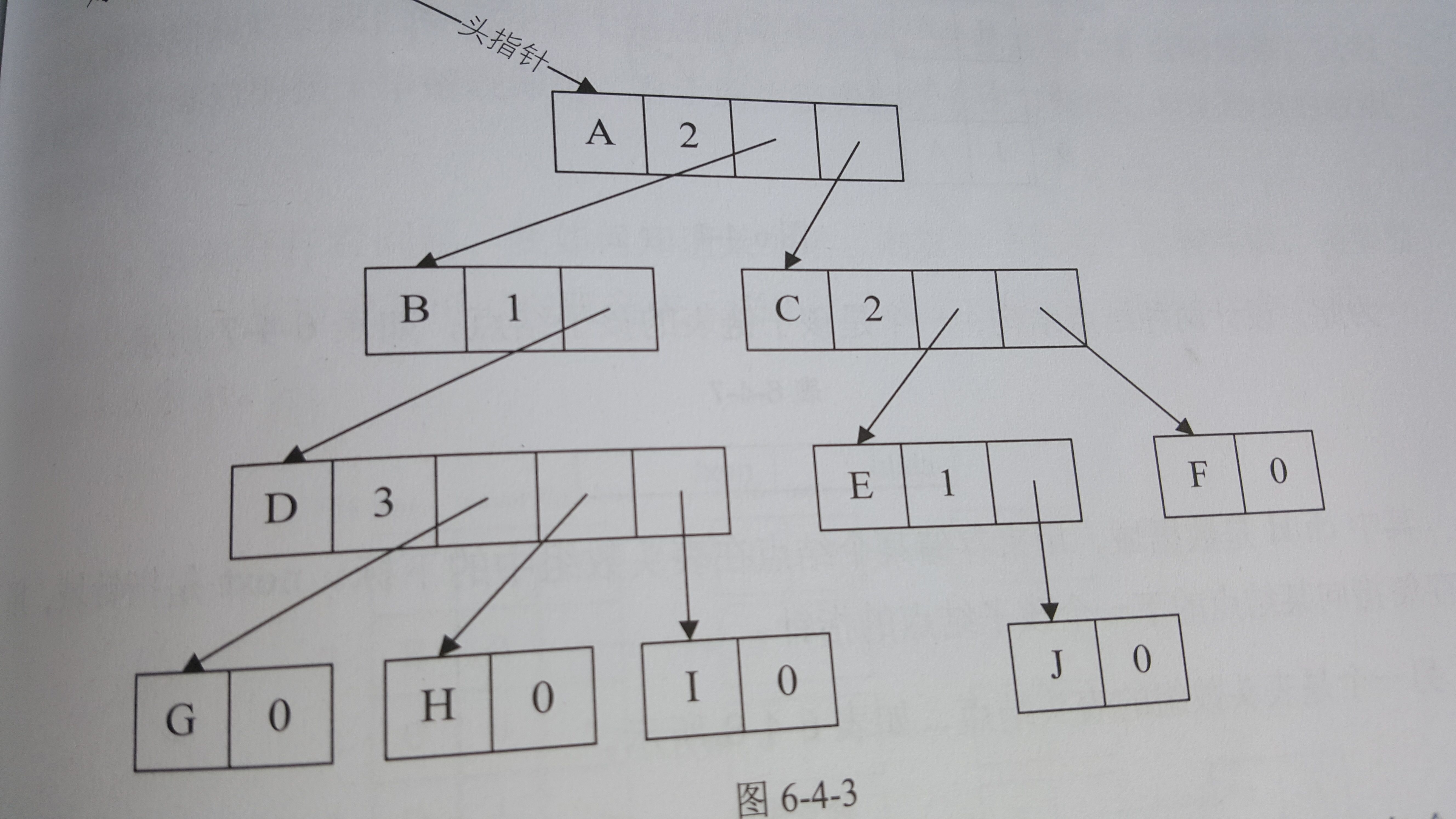
這種方案也有缺點,就是會給結點的維護帶來麻煩。所以,我們提出孩子表示法。
孩子表示法: 把每個結點的孩子結點排列起來,以單鏈表作存儲結構,則n個結點有n個孩子鏈表,如果是葉子結點則次單鏈表為空。然后n個頭指針又組成一個線性表,采用順序存儲結構,存放進一個一維數組中。如下圖。
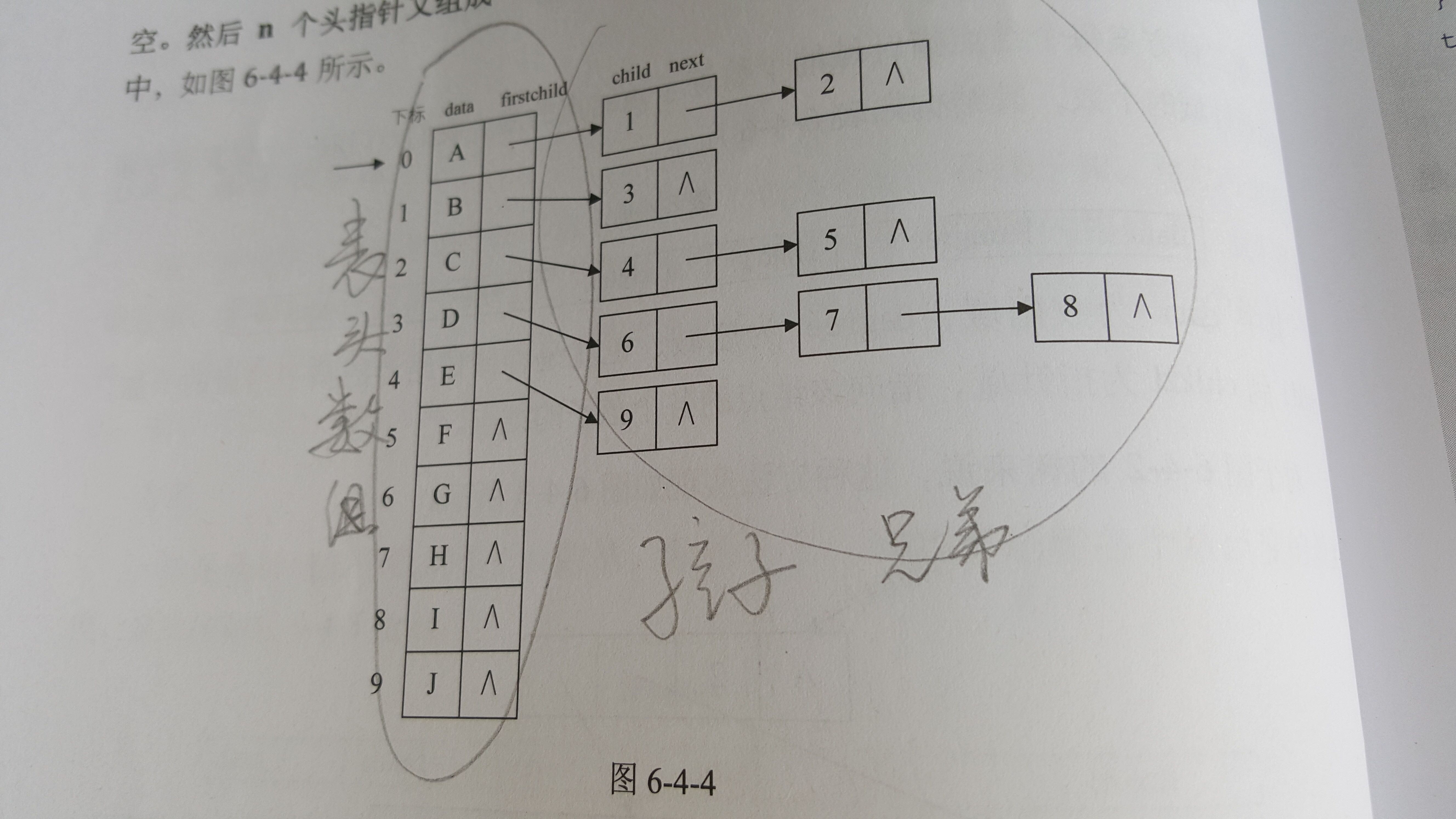
為此,設計兩種結點結構,一個是孩子鏈表的孩子結點,如下圖。
| child | next |
|---|
其中child是數據域,用來存儲某個結點在表頭數組的下標。next是指針域,用來存儲指向某結點的下一個孩子結點的指針。
另一個是表頭數組的表頭結點,如下表。
| data | firstchild |
|---|
其中data是數據域,存儲某結點的數據信息。firstchild是頭指針域,存儲該結點的孩子鏈表頭指針。
但是,這種方法也找不到某個結點的雙親。于是有了雙親孩子表示法。如下圖。

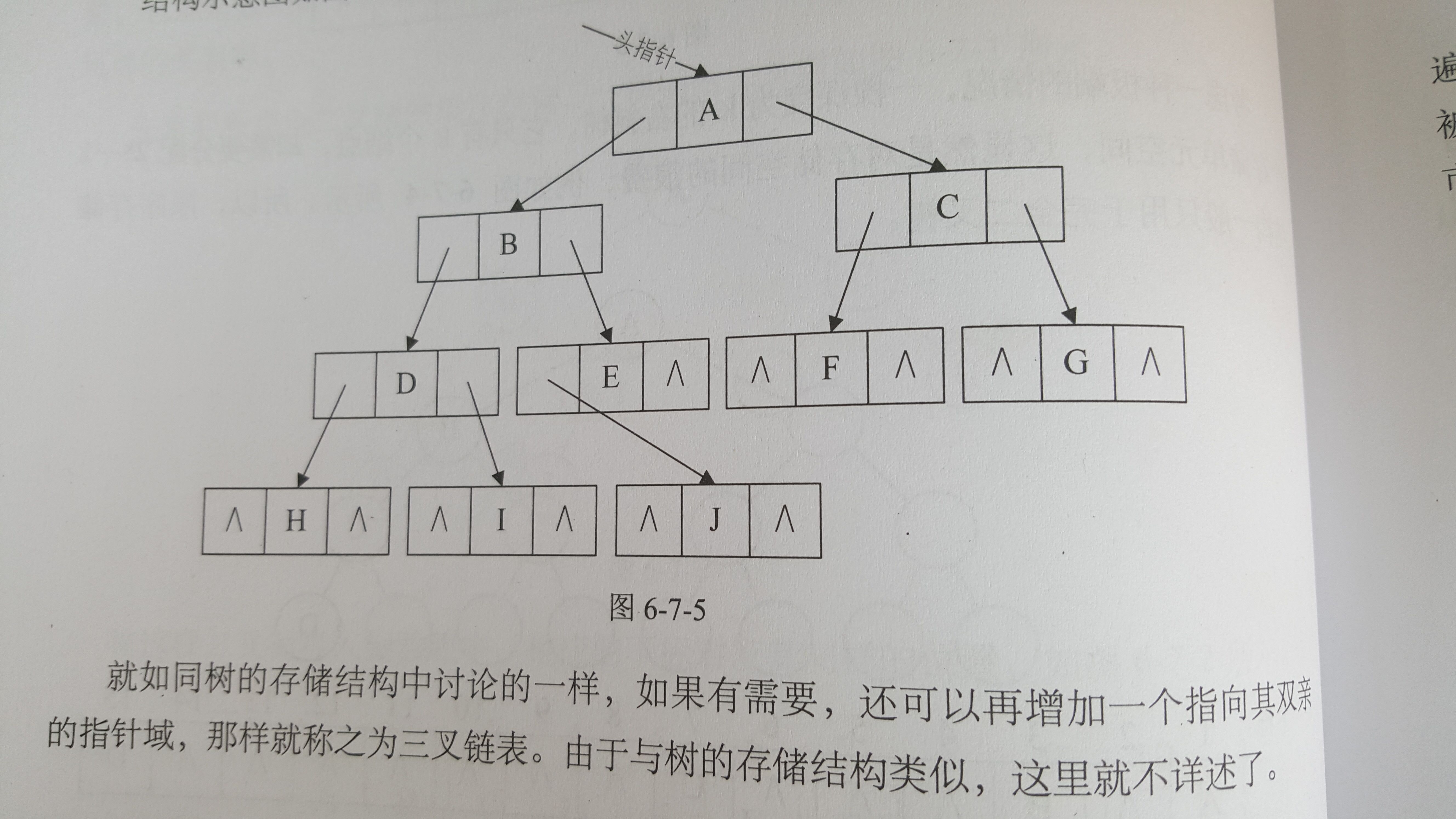
3. 孩子兄弟表示法
任意一棵樹,它的結點的第一個孩子如果存在就是唯一的,它的右兄弟如果存在也是唯一的。因此,我們設置兩個指針,分別指向該結點的第一個孩子和詞結點的右兄弟。
| data | firstchild | rightsib |
|---|
其中data是數據域,firstchild為指針域,存儲該結點的第一個孩子結點的存儲地址,rightsib是指針域,存儲該結點的右兄弟結點的存儲地址。如下圖。
三、二叉樹的定義
二叉樹(Binary Tree)是n(n>=0)個結點的有限集合,該集合或者為空集(稱為空二叉樹),或者由一個根結點和兩棵互不相交的、分別稱為根結點的左子樹和右子樹的二叉樹組成。
二叉樹的特點:
- 每個結點最多有兩棵子樹,所以二叉樹中不存在大于2的結點。注意不是只有兩棵子樹,而是最多有。沒有子樹或者有一棵子樹都是可以的。
- 左子樹和右子樹是有順序的,次序不能顛倒。就像人的左右手。
即使樹中某結點只有一棵子樹,也要區分它是左子樹還是右子樹。
二叉樹有5種基本形態:
- 空二叉樹。
- 只有一個根結點。
- 根結點只有左子樹。
- 根結點只有右子樹。
- 根結點既有左子樹又有右子樹。
斜樹:只有左子樹或者只有右子樹。是一種特殊的線性表。
滿二叉樹:所有分支結點都存在左子樹和右子樹,并且所有葉子都在同一層上。
滿二叉樹的特點有:- 葉子只能在最下一層。出現在其他層就不可能達到平衡。
- 非葉子結點的度一定是2。否則就是“缺胳膊少腿了”。
- 在同樣深度的二叉樹中,滿二叉樹的結點個數越多,葉子樹越多。
完全二叉樹:
- 葉子結點只能在最下兩層。
- 最下層的葉子一定集中在左部連續的位置。
- 倒數第二層,若有葉子結點,一定都在右部連續位置。
- 如果結點度為1,則該結點只有左孩子,即不存在右子樹的情況。
- 同樣結點數從二叉樹,完全二叉樹的深度最小。
判斷一棵樹是否是完全二叉樹,心中默默給每個結點按照滿二叉樹的結構逐層順序編號,如果編號出現空檔,就不是完全二叉樹,否則就是。
滿二叉樹是特殊的完全二叉樹。
完全二叉樹必須先滿足左后滿足右,缺的元素只能是滿二叉樹最下一層的,高度差小于或等于1。
四、二叉樹的存儲結構
(一)順序存儲結構
一般只有完全二叉樹才考慮順序存儲結構,因為完全二叉樹的嚴格性,可以充分利用順序存儲空間。其他二叉樹都會造成空間的浪費,特別是右斜樹。
(二)二叉鏈表
二叉樹每個結點最多有兩個孩子,所以為它設計一個數據域和兩個指針域,稱為二叉鏈表。
| lchild | data | rchild |
|---|
其中data是數據域,lchild和rchild都是指針域,分別存放指向左孩子和右孩子的指針。
五、遍歷二叉樹
二叉樹的遍歷(traversing binary tree)是指從根結點出發,按照某種次序一次訪問樹中所有結點,使得每個結點被訪問一次且僅被訪問一次。
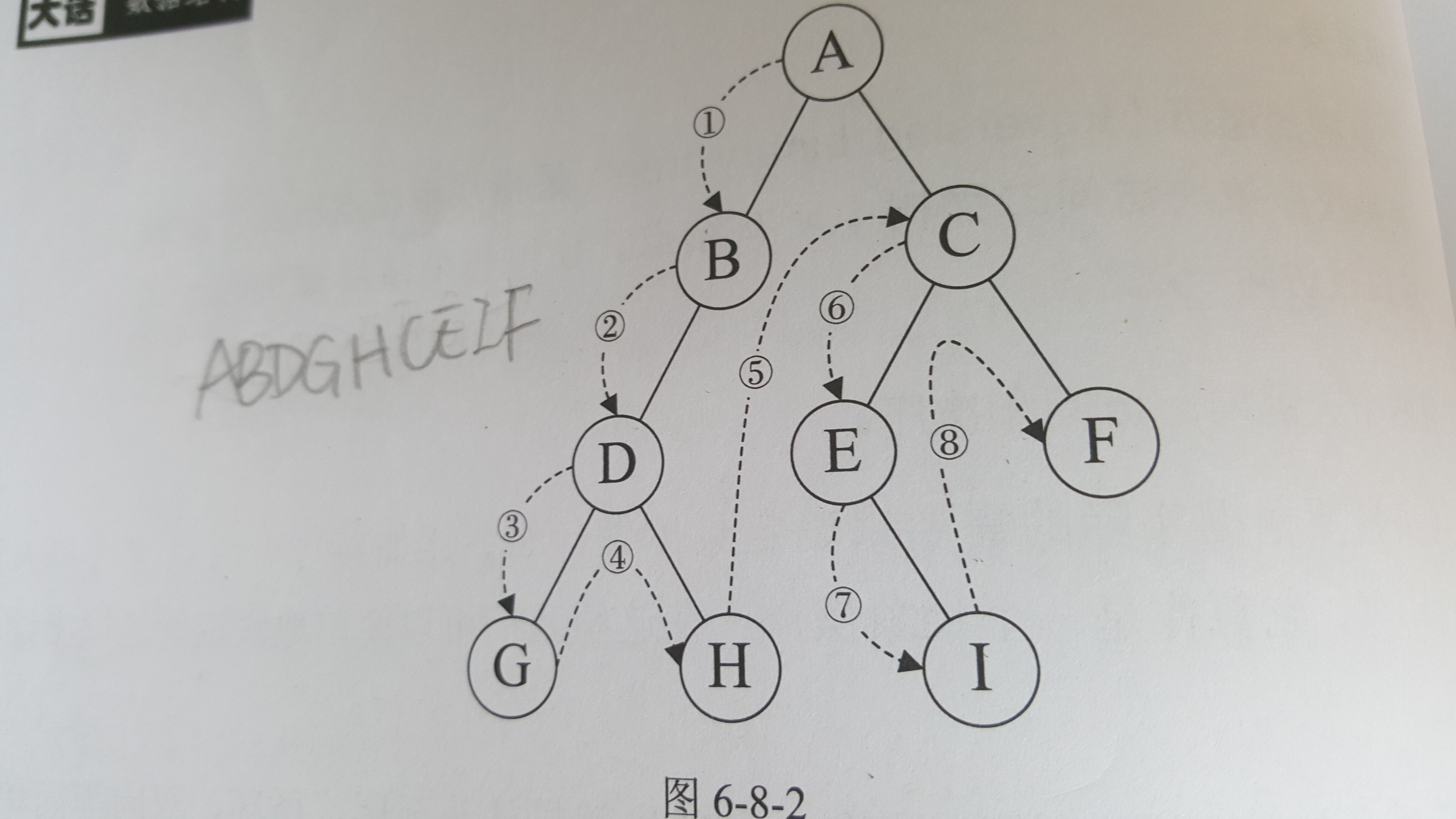
前序遍歷
根–左子樹–右子樹
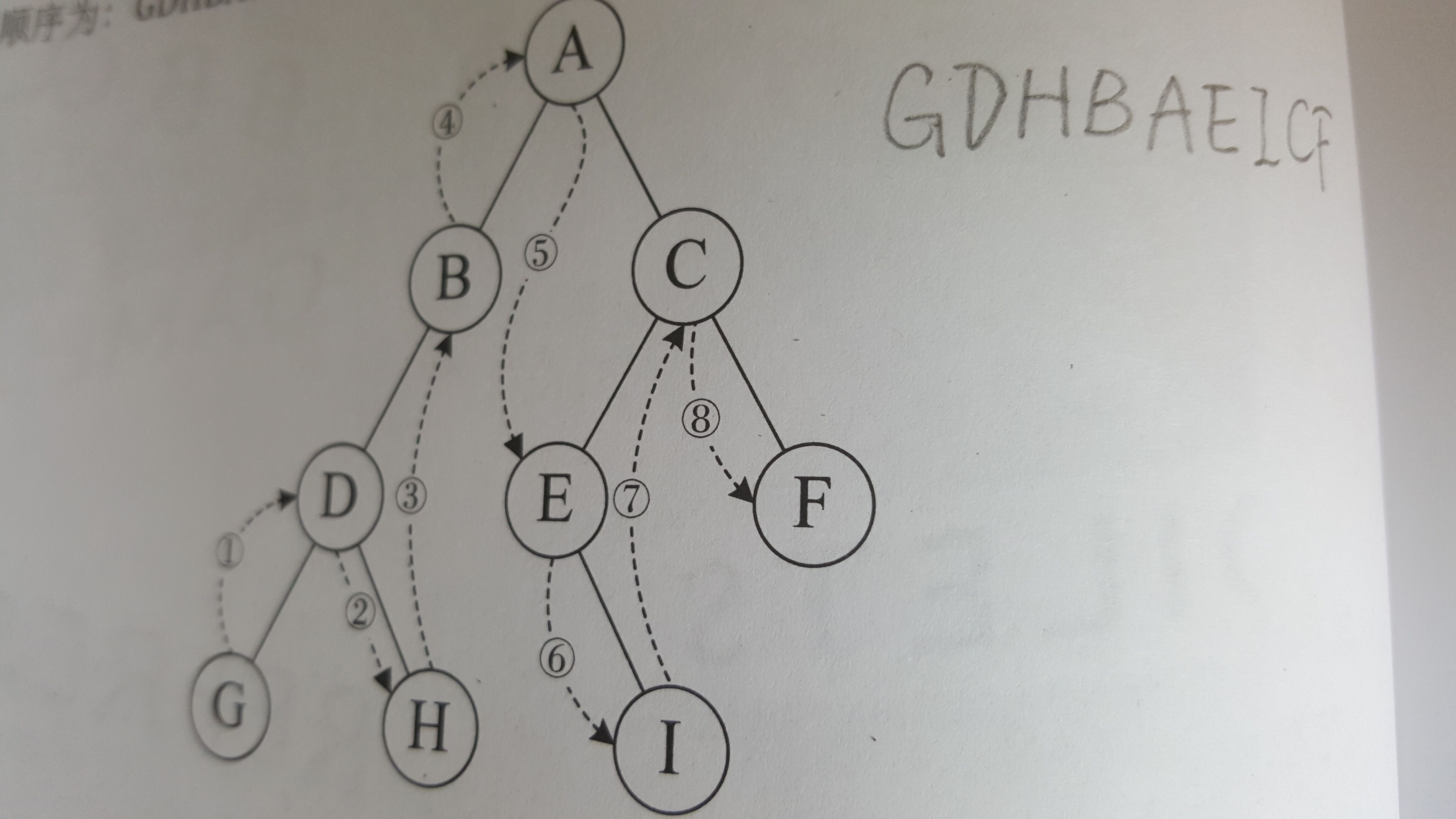
中序遍歷
左子樹–根–右子樹
后序遍歷
左子樹–右子樹–根
層序遍歷
根–第一層從左到右–第一層從左到右……
已知前序遍歷序列和中序遍歷序列,可以唯一確定一棵二叉樹。
已知后序遍歷序列和中序遍歷序列,可以唯一確定一棵二叉樹。
已知前序遍歷序列和后序遍歷序列,不可以唯一確定一棵二叉樹。
六、線索二叉樹
為了充分利用二叉鏈表的空指針,把空指針指向前驅和后繼,這種指向前驅和后繼的指針稱為線索,加上線索的二叉鏈表稱為線索鏈表,相應的二叉樹就稱為線索二叉樹。
對二叉樹一某種次序比那里時期變為線索二叉樹的過程稱作是線索化。線索化的過程就是在遍歷的過程中修改空指針的過程。
為了判別某一結點的lchild是指向左孩子還是前驅,rchild是指向右孩子還是后繼,引入ltag和rtag兩個標志域。
| lchild | ltag | data | rtag | rchild |
|---|
其中,ltag為0時指向該結點的左孩子,為1時指向該結點的前驅;rtag為0時指向該結點的右孩子,為1時指向該結點的后繼;因為對6-10-1的圖的二叉鏈表圖可以修改如下圖。
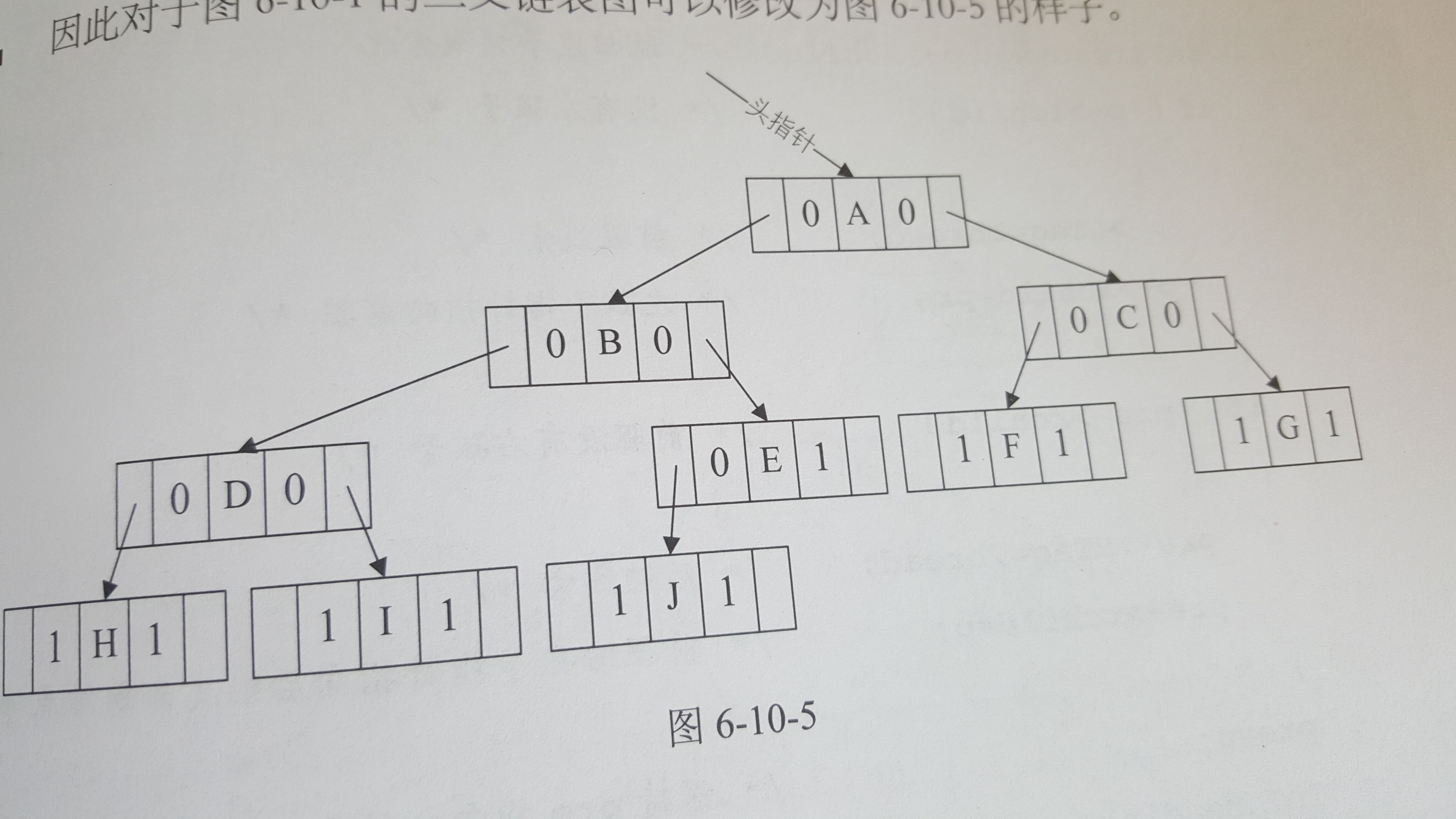
如果所用的二叉樹需經常遍歷或查找結點時需要某種遍歷序列中的前驅和后繼,那么采用線索二叉鏈表的存儲結構就是不錯的選擇。
七、二叉樹的性質
- 在一棵高度為k的二叉樹中,結點總數為至多為2k(k次方)-1
八、樹、森林與二叉樹的轉換
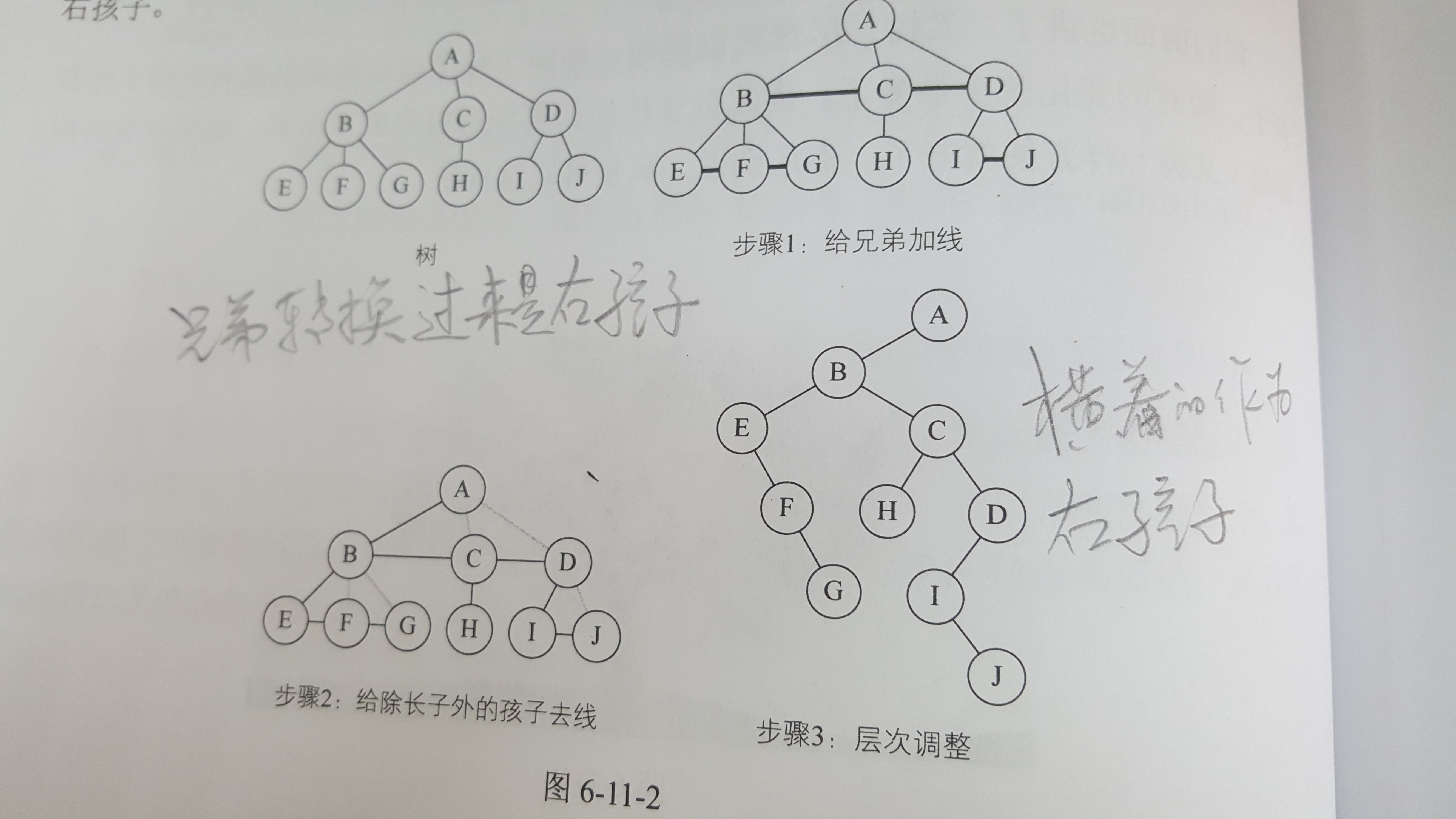
(一)樹轉化為二叉樹
1. 加線。在所有兄弟結點之間加一條連線。
2. 去線。對樹中每個結點,只保留它與第一個孩子結點的連線,刪除它與其他孩子結點之間的連線。
3. 層次調整。以樹的根結點為軸心,將整棵樹瞬時間旋轉一定的角度。使之結構層次分明。之一第一個孩子是二叉樹結點的左孩子,兄弟轉換過來的孩子是結點的右孩子。
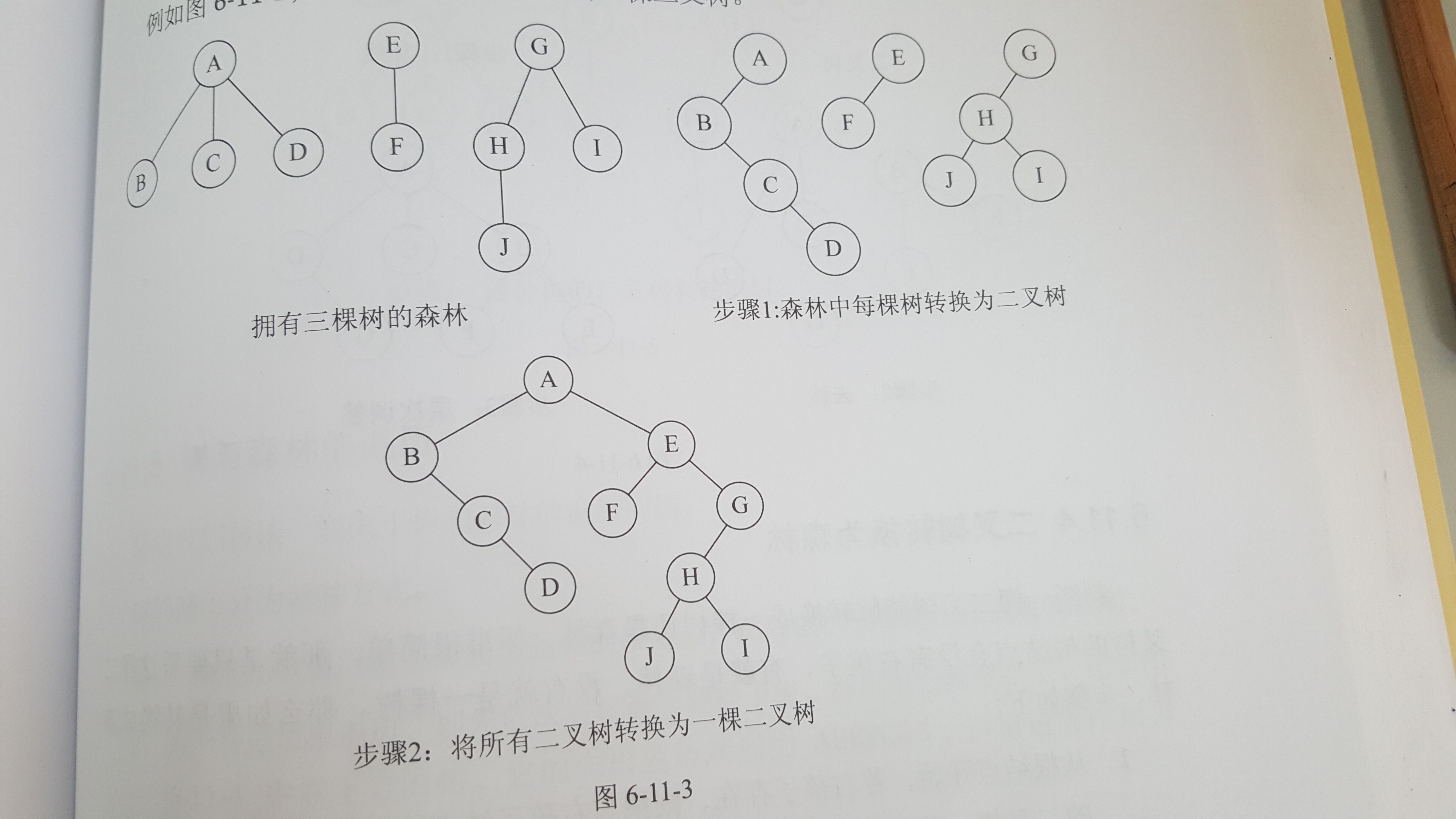
(二)森林轉換為二叉樹
森林是由若干棵樹組成的,所以完全可以理解為,森林中的每一棵樹都是兄弟,可以按照兄弟的處理辦法來操作,如下:
1. 把每個樹轉換為二叉樹;
2. 第一棵樹不動,從第二棵二叉樹開始,依次把后一棵二叉樹的根結點作為前一棵二叉樹的根結點的右孩子,用連線連接起來。當多有的二叉樹連接起來后就得到森林轉化的二叉樹。
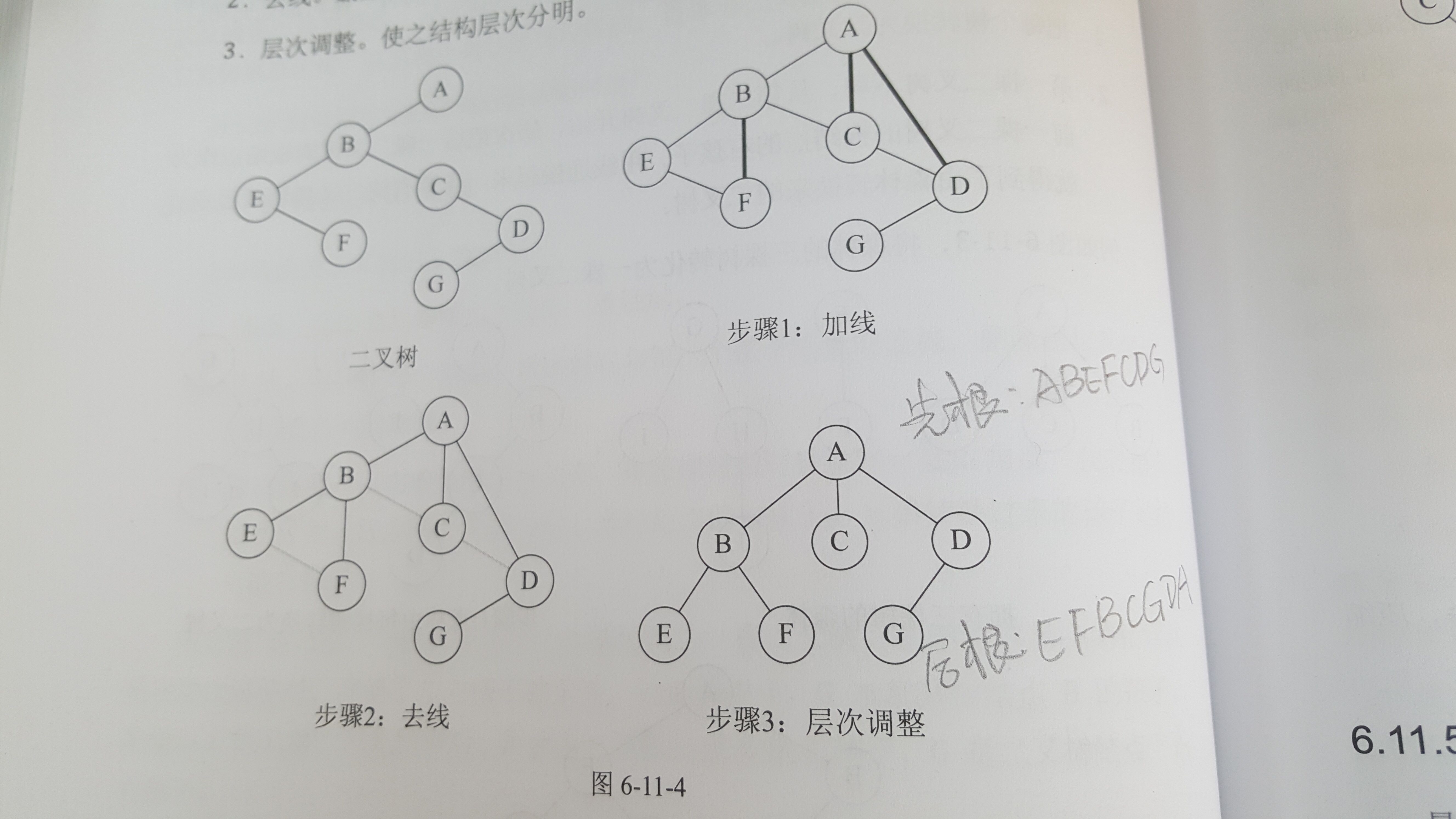
(三)二叉樹轉換為樹
二叉樹轉換為樹是樹轉換為二叉樹的逆過程。
1. 加線。若某結點的左孩子結點存在,則將這個左孩子的右孩子結點、右孩子的右孩子結點、右孩子的右孩子的右孩子的結點……哈,反正就是左孩子的n個右孩子結點都作為此結點的孩子。將該結點與這些右孩子結點用線連接起來。
2. 去線。刪除原二叉樹中所有結點與其右孩子結點的連線。
3. 層次調整。使之結構層次分明。
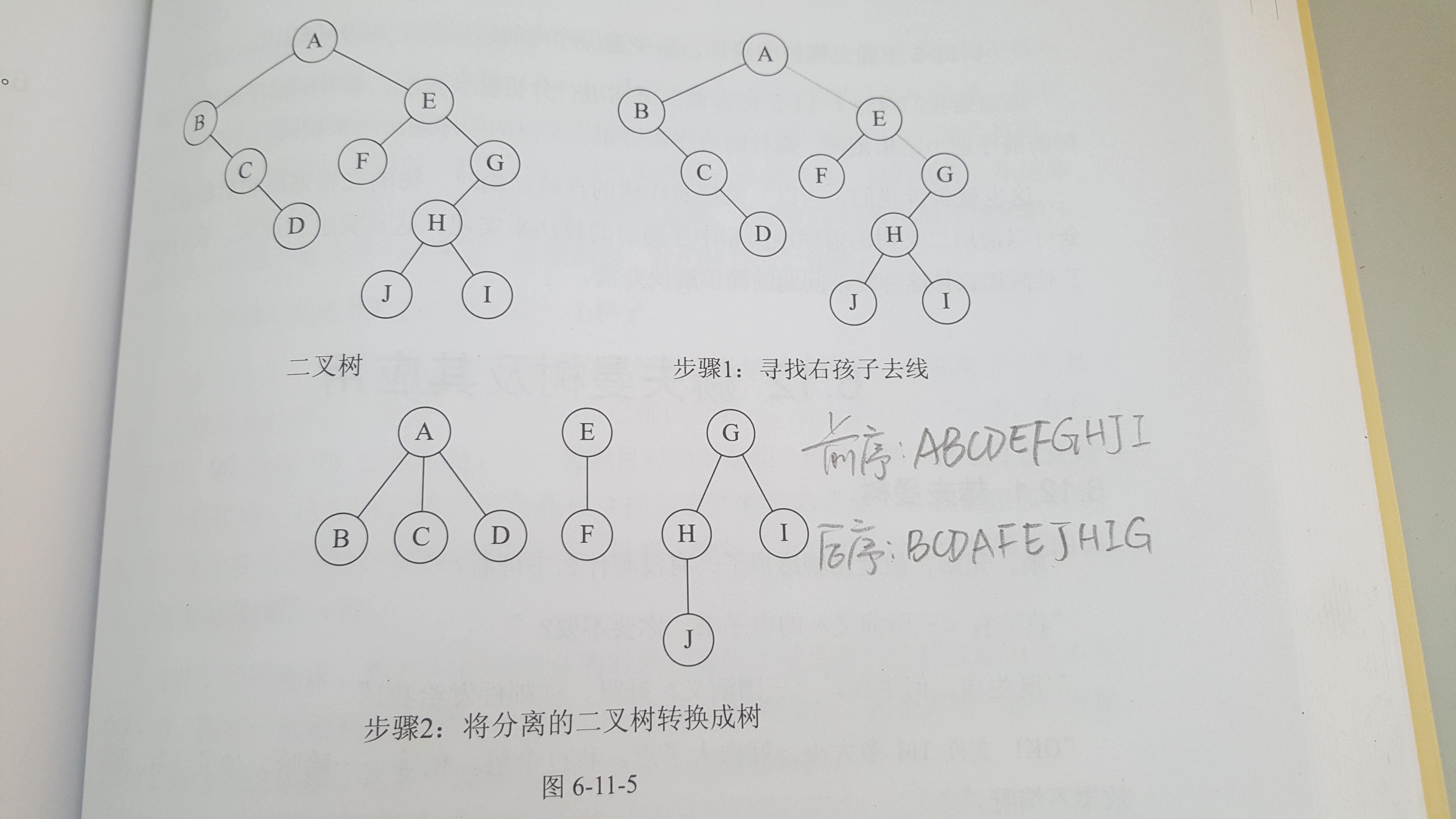
(四)二叉樹轉換為森林
判斷一棵樹是否能轉換為一棵樹還是森林,就看它是否有右結點,若有,就可以轉為森林,否則,就是一棵樹。
1. 從根結點開始,若右孩子存在,則把與右孩子結點的連線刪除,再查看分離后的二叉樹,若右孩子存在,則連線刪除……,直到所有右孩子連線都刪除為止,得到分離的二叉樹。
2. 再將每棵分離后的二叉樹轉換為樹即可。
(五)樹與森林的遍歷
樹的遍歷分為兩種方式:
1. 一種是先根遍歷樹,即先訪問樹的根結點,然后依次先根遍歷根的每棵子樹。
2. 另一種是后根遍歷,即先依次后根遍歷每棵子樹,然后再訪問根結點。
森里的遍歷方式也分為兩種方式:
1. 前序遍歷:先訪問森林中第一棵樹的根結點,然后再依次先跟遍歷根的每棵子樹,再依次用同樣方式遍歷除去每一棵樹的剩余樹構成的森林。
2. 后序遍歷:先訪問森林中第一棵樹,后根遍歷的方式遍歷每棵子樹,然后再訪問根結點,再依次同樣方式遍歷除去第一棵樹的剩余樹構成的森林。
樹和森林的遍歷可參看(三)(四)圖中的筆記。
神奇的是,森林的前序遍歷和二叉樹的前序遍歷結果相同,森林的后序遍歷和二叉樹的中序遍歷結果相同。這也就告訴我們,當以二叉鏈表作樹的存儲結構時,樹的先根遍歷和后根遍歷完全可以借用二叉樹的前序遍歷和中序遍歷的算法來實現。
九、赫夫曼樹
赫夫曼樹:帶全路徑長度WPL最小的二叉樹。
先取最小權值的結點作為葉子結點,逐級遞增就能構造出哈夫曼樹。把左結點標為0,右結點標為1,就能構造出赫夫曼編碼。
十、題目
- 某棵完全二叉樹上有699個節點,則該二叉樹的葉子節點數為(350)。
解析:n0=n2+1;
n=n0+n1+n2=n0+n1+n0-1=699
由于完全二叉樹中度為1的節點只有0個或1個兩種情況,所以,將0或1帶入上面公式,整理后得: n0=(n+1)/2或者n0=n/2; 看看n是否能被2整除,能則用n0=n/2。否則用n0=(n+1)/2 既葉子節點為n0=(n+1)/2=350。 - 一棵有124個葉節點的完全二叉樹,最多有(248 )個節點。
解析:n0 = n2 + 1,于是度為2的結點個數123個
完全二叉樹中度為1結點個數最多1個
因此該完全二叉樹中結點最多有123 + 1 + 124 = 248個