圖(Graph)是由定點的又窮非空集合和頂點之間邊的集合組成,通常表示為:G(V,E),其中,G表示一個圖,V是圖G中頂點的集合,E是圖G中邊的集合。
一、各種圖的定義
圖按是否有方向分可分為有向圖和無向圖。有向邊用尖括號“<>”表示,無向邊用小括號“()”表示。
簡單圖:無環無重復邊。我們以下討論的都是簡單圖。
無向完全圖:任意兩個頂點之間都存在邊。
含有n個頂點的無向完全圖有n*(n-1)/2條邊。
有向完全圖:任意兩個頂點之間都存在方向互為相反的兩條弧。
含有n個頂點的有向完全圖有n*(n-1)條邊。
網:帶權的圖。
回路或環:第一個頂點到最后一個頂點相同的路徑稱為回路或環。
簡單路徑:序列中頂點不重復出現的路徑。
簡單回路或簡單環:除了第一個頂點和最后一個頂點之外,其余頂點不重復出現的回路。
連通圖:任意兩個頂點之間互通。
連通分量:無向圖中極大連通子圖。(要是子圖、子圖要是連通的、連通子圖含有極大頂點數、具有極大定點數的連通子圖包含依附于這些頂點的所有邊)
二、圖的存儲方式
(一)鄰接矩陣
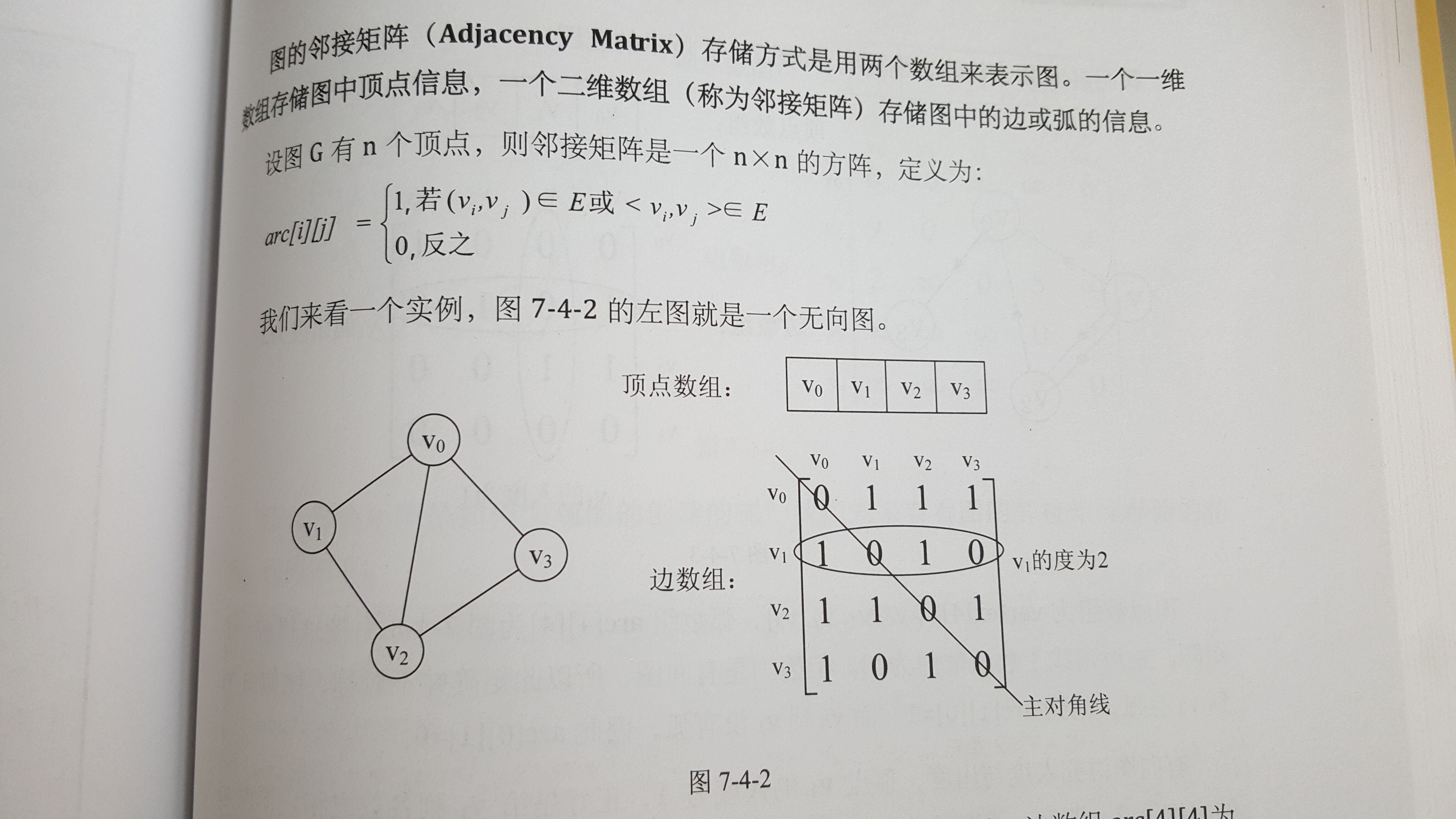
鄰接矩陣是頂點和邊的二維數組,若頂點間存在邊,則標作1,否則,標作0。
橫著的和是該頂點的度。
(二)鄰接表
數組與鏈表相結合的存儲方法。

但在有向圖中,一般只關注到出度問題,逆連接表關注到的是入度的問題。
(三)十字鏈表
把鄰接表和逆鄰接表結合。
(四)鄰接多重表
三、圖的遍歷
圖的遍歷指的是從圖中某一頂點出發訪遍圖中其余頂點,且使每一個頂點僅被訪問一次。
(一)深度優先遍歷
深度優先遍歷(Depth_First_Search)DFS,顧名思義,就是從一個頂點出發,往最深里找。
廣度優先遍歷(Breath_First_Search)BFS,也就是從一個頂點出發,一層層找。
它們的時間復雜度是一樣的,只是結點訪問的順序不一樣。
四、最小生成樹
最小生成樹:構造連通網的最小代價生成樹。
普里姆算法:從一個點出發,找連通的。
克魯斯卡爾算法:先找最短的邊。
五、最短路徑
迪杰斯特拉算法:從一個頂點出發,逐漸找權最小的。
弗洛伊德算法
如果要求所有點到其他點的最短路徑,選弗洛伊德算法。
六、關鍵路徑
一個個去掉度為0的頂點。



















