查找（Searching）是根據給定的某個值，在查找表中確定一個其關鍵字等于給定值的數據元素（或記錄）。

一、順序表查找

順序查找又叫線性查找，是最基本的查找技術，它的查找過程是：從表中第一個（或最后一個）記錄開始，逐個記性記錄的關鍵字和給定值比較，若某個記錄的關鍵字和給定值相等，則查找陳宮，找到所查的記錄；如果直到最后一個（或第一個）記錄，其關鍵字和給定值比較都不等時，則表中沒有所查的記錄，查找不成功。
時間復雜度為O(n)。

二、有序表查找

（一）折半查找
折半查找又稱二分查找。它的前提是線性表中的記錄必須是關鍵碼有序（通常是從小到大有序），線性表必須采用順序存儲。
折半查找的基本思想是：在有序表中，取中間記錄作為比較對象，若給定值與中間記錄的關鍵字相等，則查找成功；若給定值小于中間記錄的關鍵字，則在中間記錄的左半區繼續查找；若給定值大于中間記錄的關鍵字，則在中間記錄的右半區繼續查找。不斷重復上述過程，直到查找成功，或所有查找區域無記錄，查找失敗為止。
時間復雜度為O(logn）

（二）插值查找
插值查找的關鍵是根據要查找的關鍵字key與查找表中最大最小記錄的關鍵字比較后的查找方法，其核心就在于插值的計算公式（key-a[low]）/(a[high]-a[low])。
從時間復雜度上看，它也是O(logn），但對于表長比較大，而關鍵字分布又比較均勻的查找表來說，插值查找算法的平均性能比這般查找要好很多。

（三）斐波那契查找

三、線性索引查找

索引是把一個關鍵字與它對應的記錄相關聯的過程。一個索引由若干個索引構成，每個索引項至少應包含關鍵字和其對應的記錄在存儲器中的位置等信息。
線性索引是將索引項集合組織委員線性結構，稱為索引表。 以下重點介紹三種線性索引：稠密索引、分塊索引、倒排索引。

（一）稠密索引
稠密索引是指在線性索引中，將數據集中的每個記錄對應一個索引項。
稠密索引要應對的可能是成千上萬的數據，因此對于稠密索引這個索引表來說，索引項一定是按照關鍵碼有序的排列。

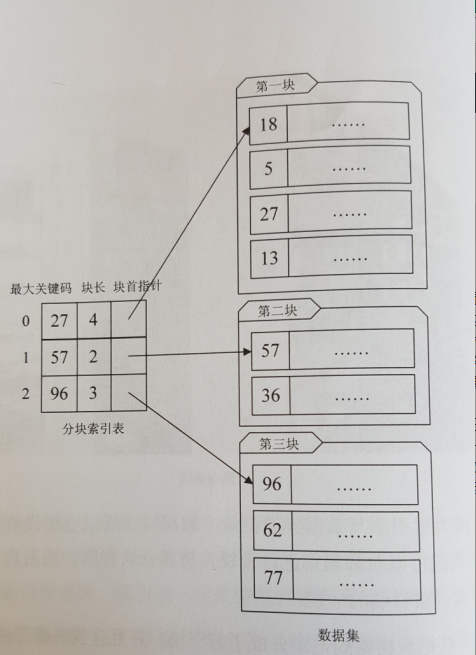
（二）分塊索引
例子：圖書館藏書。
分塊有序，是把數據集的記錄分成了若干塊，將每塊對應一個索引項，并且這些塊需要滿足：
（1）塊內無序，即每一塊內的記錄不要求有序。當然，你如果能夠讓塊內有序對查找來說更理想，不過這就要付出大量時間和空間代價，因此通常我們不要求快內有序。
（2）塊間有序，例如，要求第二塊所有記錄的關鍵字均要大于第一塊中所有記錄的關鍵字，第三塊所有記錄的關鍵字均要大于第二塊的所有記錄關鍵字……因為只有塊間有序，才有可能在查找時帶來效率。
分塊索引的索引項結構分為三個數據項：
（1）最大關鍵碼，存儲每一塊中的最大關鍵字；
（2）存儲了塊中的記錄個數，以便循環時用；
（3）用于指向塊首數據元素的指針，便于開始對這一塊中記錄進行遍歷。

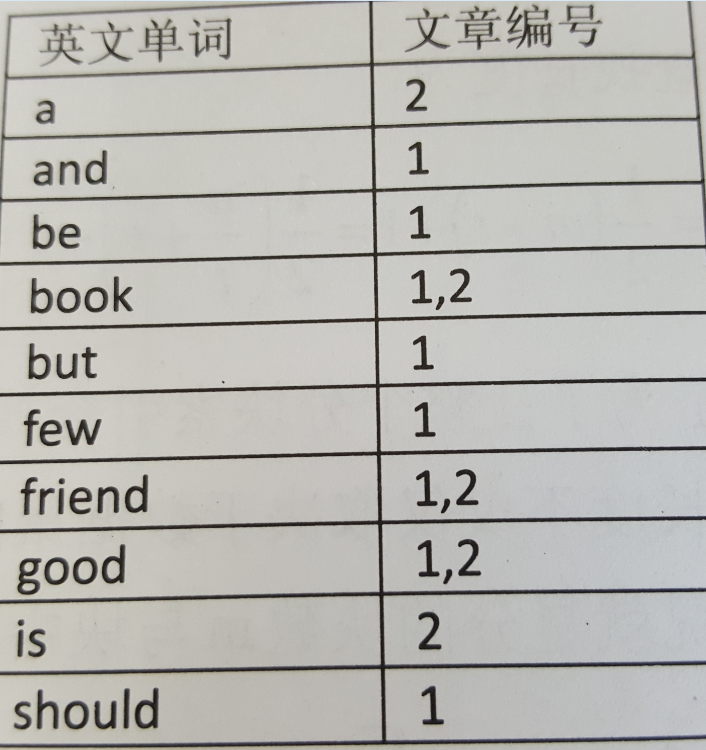
（三）倒排索引
網頁搜索一般用的就是倒排索引。
倒排索引的通用結構是：

• 次關鍵碼（如“英文單詞”）
• 記錄號表（如“文章編號”）

記錄號表存儲具有相同次關鍵字的所有記錄的記錄號（可以是指向記錄的指針或者是該記錄的主關鍵字）

四、二叉排序樹

二叉排序樹又稱為二叉查找樹。它或者是一棵空樹，或者是具有下列性質的二叉樹。

• 若它的左子樹不空，則左子樹上所有結點的值均小于它的根結構的值；
• 若它的右子樹不空，則右子樹上所有結點的值均大于它的根結構的值；
• 它的左、右子樹也分別為二叉排序樹。
  按中序遍歷它是棵有序樹。

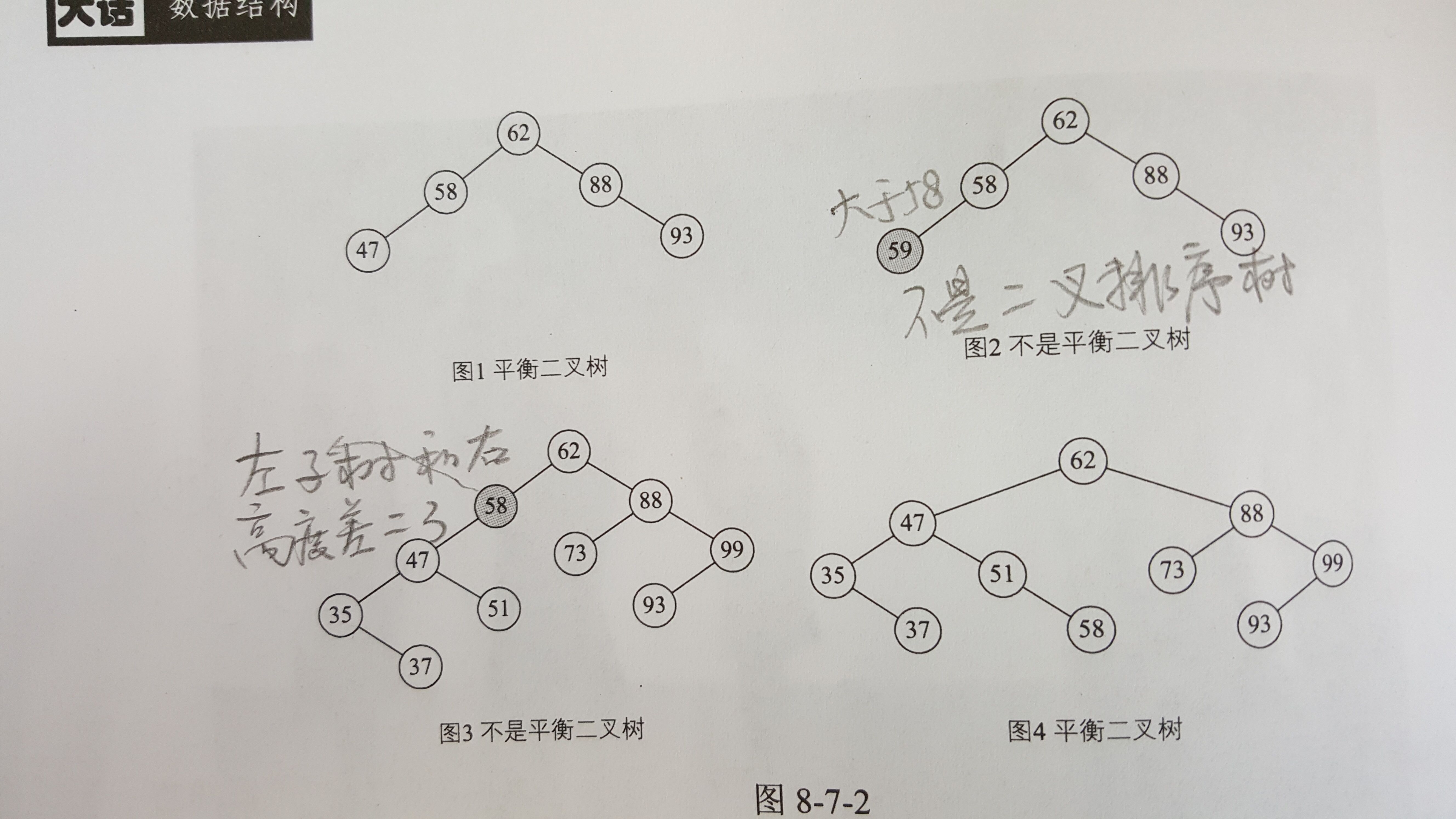
五、平衡二叉樹（AVL樹）

平衡二叉樹，是一種二叉排序樹，其中每一個結點的左子樹和右子樹的高度差至多等于1。

六、多路查找樹（B樹）

多路查找樹，其每一個結點的孩子書可以多于兩個，且每一個結點處可以存儲多個元素。

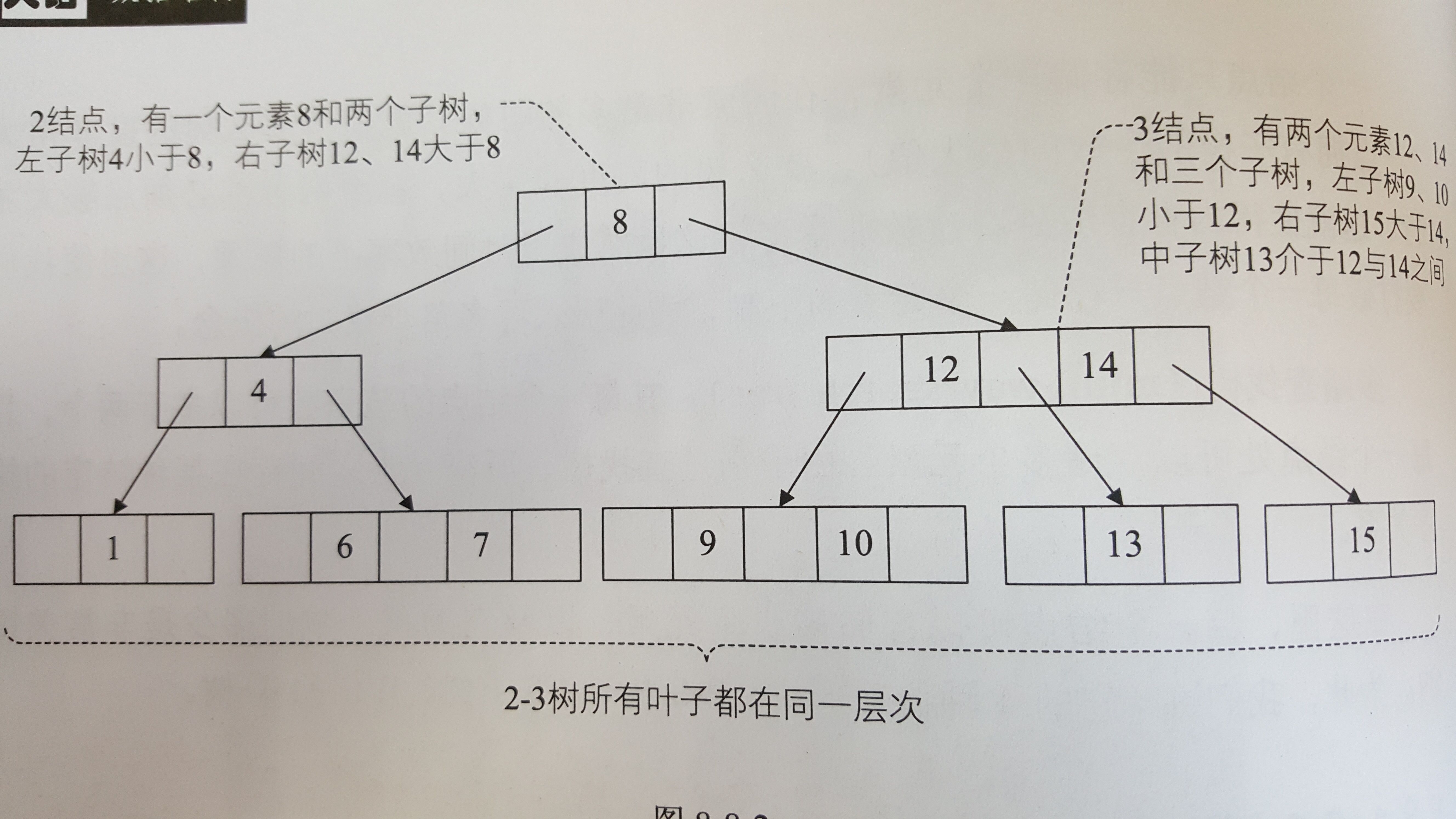
（一）2-3樹
2-3樹是一棵多路查找樹：其中的每一個結點都具有兩個孩子（稱為2結點）或三個孩子（稱為3結點）。
一個2結點包含一個元素和兩個孩子（或沒有孩子）。
一個3結點包含一小一大兩個元素和三個孩子（或沒有孩子）。

（二）2-3-4樹
2-3-4樹是2-3樹的擴展，包括了4個結點的使用。一個結點包含小中大三個元素和四個孩子（或沒有孩子）。

（三）B樹
B樹是一種平衡的多路查找樹，2-3樹和2-3-4樹都是B樹的特例。結點最大的孩子數目稱為B樹的階，因此，2-3樹是3階的B樹，2-3-4樹是4階的B樹。

（四）B+樹

七、散列表查找（哈希表）概述

散列技術是在記錄的存儲位置和它的關鍵字之間建立一個確定的對應關系f，使得每個關鍵字key對應一個存儲位置f（key）。查找時，根據這個確定的對應關系找到給定值key的映射f（key），若查找集合中存在這個記錄，則必定在f（key）的位置上。
我們把上述的對應關系f稱為散列函數，又稱為哈希函數。采用散列技術將記錄存儲在一塊連續的存儲空間中，這塊連續存儲空間稱為散列表后哈希表。