一、為啥要有神經網絡？

在前面的幾篇博客中，很容易知道我們處理的都是線性的數據，例如：線性回歸和邏輯回歸，都是線性的算法
但是，實際上日常生活中所遇到的數據或者問題絕大多數還是非線性的
一般面對非線性數據，我們可以采用多項式回歸進行處理，詳細內容可以參考博文：五、線性回歸和多項式回歸實現
說白了就是改變橫縱坐標，是得數據線性化。例如：工資和年齡呈拋物線關系，但是工資和年齡的平方則呈線性關系，此時就可以將年齡的平方作為變量進行線性處理。

神經網絡是非線性的算法！！！
為啥捏？

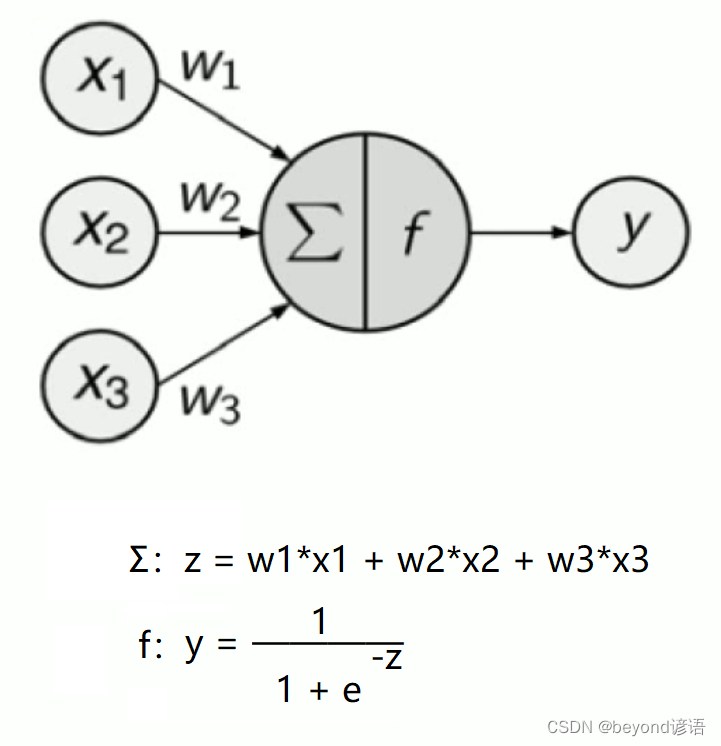
舉個栗子：
當你傳入x1,x2,x3三個數據時，對應三個權重參數，代入求和，即得到Σ，這一步是線性的，得到z
關鍵點來了！！！f為激活函數，這個函數很關鍵，因為它不是線性函數！！！
常用的激活函數有很多，這里假設使用的激活函數為sigmoid函數，將求和的值代入sigmoid函數中得y，由于激活函數是非線性的，z是線性的，代入得到的最終的結果y肯定是非線性的！！！
故稱神經網絡是非線性的算法。

神經網絡是非線性的算法可以解決實際生活中的非線性數據所帶來的一系列問題，故有需求才會有存在。

想當年Google的alphago大戰李世石，就是用的神經網絡。程序員搬了14臺服務器組成一個集群，前三局alphago贏了，但是第四局的時候輸了，這時候程序員喊暫停，說要調整參數，調整參數，這么多權重你知道調啥？神經網絡里面的隱藏層都是黑盒子，鬧呢？實際上他們應該是初始化參數，用一開始的模型參數，alphago為啥第四局會輸？主要是學習過擬合了。alphago一邊和李世石下棋一邊會去學習，重新更新權重參數。此時程序員初始化模型，后幾局alphago取得勝利。

二、常見的激活函數

1，Sigmoid激活函數

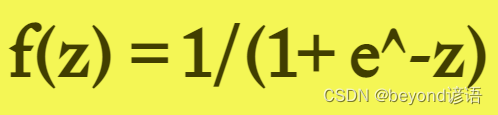
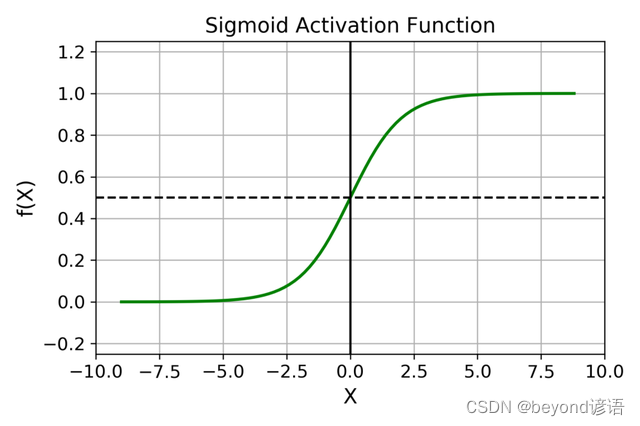
2，Tanh / 雙曲正切激活函數

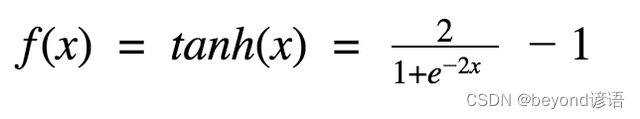
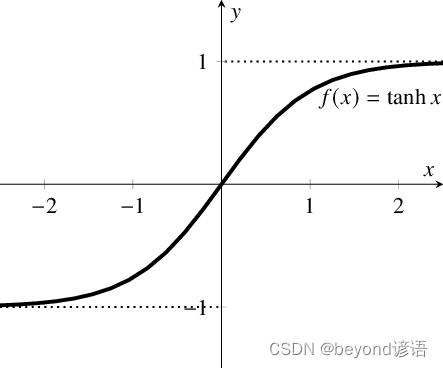
3，ReLU 激活函數

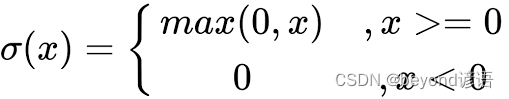
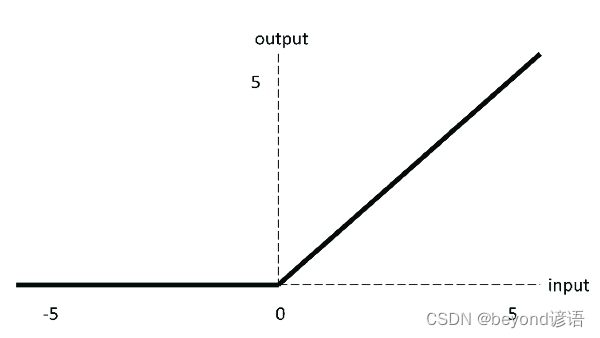
4，ELU激活函數

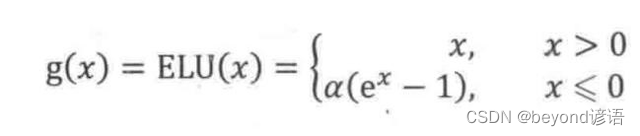
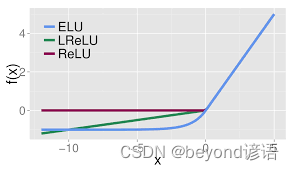
5，PReLU（Parametric ReLU）激活函數

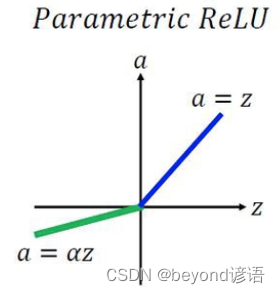
6，Softmax激活函數

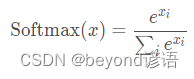
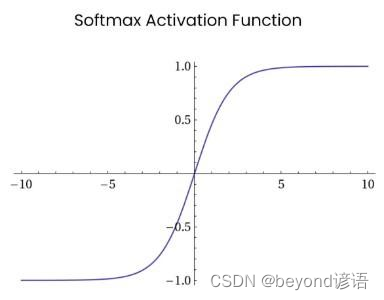
四、隱藏層的含義

大年初一，你去上別人家房頂感嘆人生，最后房頂塌了，傷到人了，你看你老媽會不會打你就完事了
大年初一，你去上自家房頂摘菜幫老媽做家務，你再看看你會不會挨打

大年初二，你閑著沒事玩火，還口嗨，我飲酒點孤燈，最后造成火災傷到其他人了，你看你老媽會不會打你就完事了
大年初二，你玩火去幫老媽做飯，你再看看你會不會挨打

大年初三，你又閑了，拿起家里面的菜刀跑出去，來尋找你的青春，最后腦子抽筋傷到人了，你覺得你媽會不會揍你
大年初三，你動刀幫老媽做飯，再看看你會不會挨打

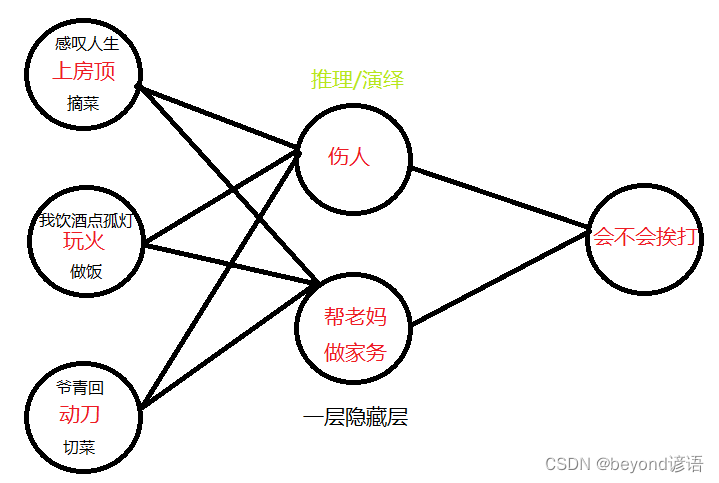
這里的隱藏層的作用就起到了推理演繹的作用，讓機器更加容易的進行判斷。
隱藏層越多，模型的推理演繹越多，也就是模型想的越多，預測結果也就會越準。

五、神經網絡相關概念

機器學習–擬人

有監督的機器學習：
多元線性回歸＝＝＝回歸/預測
邏輯回歸＝＝＝分類

神經網絡(仿生)＝＝＝預測
神經網絡是非線性的算法，非線性的算法可以來解決更加復雜的問題
神經網絡算法也是后面深度學習的時候的基礎，例如：
ANN artificial neural network
MLP multiple layer percepton
CNN 卷積神經網絡
RNN 循環神經網絡
… …

Ⅰ，神經網絡需要考慮的基本要素有哪些？

答：1，激活函數的選擇。對應神經元里面的邏輯，包括兩部分，相乘相加(Σ)和非線性的變化(f激活函數)，相乘相加是固定不變的；非線性的變化(f激活函數)可以有很多選擇，根據效果來
2，網絡拓撲結構。處理更加復雜的問題，就需要更多的網絡層，就需要每層上面設置更多的人工神經元
3，在去求解神經網絡模型(w0,w1,w2…wn)的時候，選擇什么樣優化算法，SGD一樣適用！

Ⅱ，激活函數有哪些？

答：1，Sigmoid函數，0到1之間 2，Tangent函數，-1到1之間 3，Relu函數，max(0,x)

Ⅲ，神經網絡算法的隱藏層意義何在？

答：1，如果有隱藏層的話，就多了推理有演繹的能力
2，每多一個隱藏層，推理和演繹的過程更多，考慮的更深入
3，隱藏層的隱藏節點如果比之前的層上面的節點數要多，相當于進行了升維，考慮的因素更多，考慮的更全面
4，隱藏層的隱藏節點如果比之前的層上面的節點數要少，相當于進行了降維，去前面進行了歸納總結

六、項目實戰

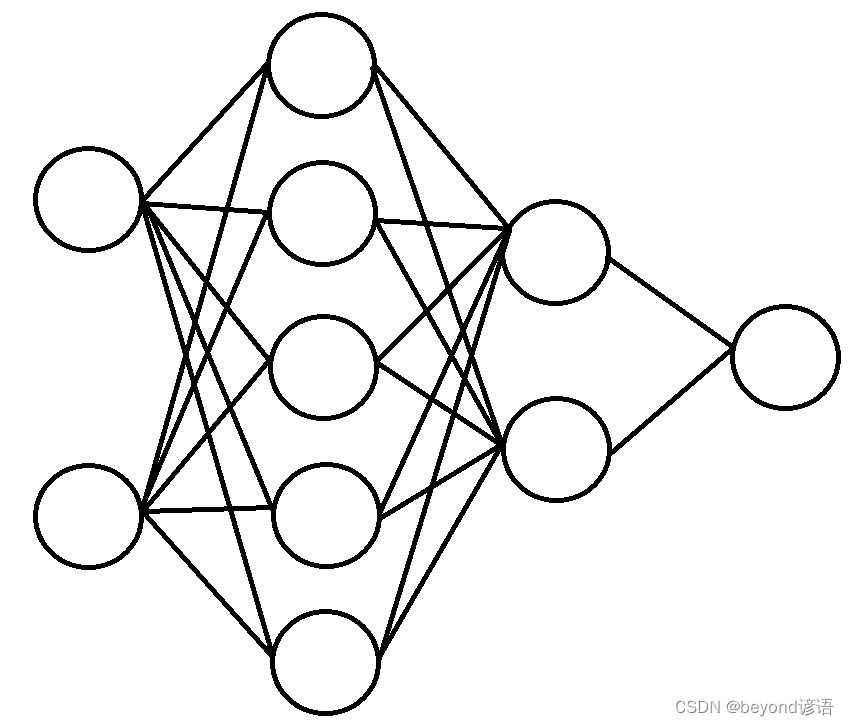
訓練一個兩次隱藏層(5個、2個)，來進行訓練，最后判斷輸入的結果是0還是1

from sklearn.neural_network import MLPClassifier#訓練集參數
X = [[0., 0.], [1., 1.]]#輸入層有兩個輸入節點
y = [0, 1]#輸出層只有一個輸出節點
"""
solver='sgd'                優化算法，這里使用的是隨機梯度下降法
alpha=1e-5                  梯度下降那個系數，表示步長
activation='logistic'       激活函數，這里使用的是sigmoid函數
hidden_layer_sizes=(5, 2)   兩層隱藏層，分別是5個和2個
max_iter=2000               最大迭代次數
tol=1e-4                    閾值，迭代終止條件
"""
clf = MLPClassifier(solver='sgd', alpha=1e-5, activation='logistic', hidden_layer_sizes=(5, 2), max_iter=2000, tol=1e-4)
clf.fit(X, y)#測試集參數
predicted_value = clf.predict([[2., 2.], [-1., -2.]])
print(predicted_value)
predicted_proba = clf.predict_proba([[2., 2.], [-1., -2.]])
print(predicted_proba)print([coef.shape for coef in clf.coefs_])
print([coef for coef in clf.coefs_])

輸出結果：

"""
[1 1]
[[0.42020492 0.57979508][0.41408929 0.58591071]]
[(2, 5), (5, 2), (2, 1)]
[array([[ 0.08530062, -0.52124089, -0.29367687,  0.07361264,  0.02156327],[ 0.46945464,  0.22892193,  0.15913923, -0.52165397,  0.44346639]]), array([[-0.02538695,  0.02746434],[-0.12493617,  0.2892428 ],[-0.34109646,  0.05022483],[ 0.02789934, -0.49890685],[ 0.35519161,  0.46174166]]), array([[ 0.31453746],[-0.4271511 ]])]"""

網絡模型如下：