數據結構初階--二叉樹的鏈式結構

目錄

一.二叉樹鏈式結構的概念

二.二叉樹鏈式結構的功能實現

2.1.鏈式二叉樹的定義

2.2.鏈式二叉樹的構建

2.3.鏈式二叉樹的遍歷

2.3.1.先序遍歷

2.3.2.中序遍歷

2.3.3.后序遍歷

2.3.4.層序遍歷

2.4.鏈式二叉樹的求二叉樹的結點數量

法一：計數法

法二：分治法

2.5.鏈式二叉樹的求二叉樹的葉子結點數量

2.6.鏈式二叉樹的求二叉樹第k層結點的數量

2.7.鏈式二叉樹的求二叉樹的高度

2.8.鏈式二叉樹的查找二叉樹中值為x的結點

2.9.鏈式二叉樹的判斷二叉樹是否是完全二叉樹

2.10.鏈式二叉樹的二叉樹的銷毀

三.二叉樹基礎OJ練習

題一：單值二叉樹

題二：相同的樹

題三：對稱二叉樹

題四：另一棵樹的子樹

題五：二叉樹的前序遍歷

題六：二叉樹遍歷

前置說明：

在學習二叉樹的基本操作之前，需要先創建一棵二叉樹，然后才能學習其相關的基本操作。由于現在對于二叉樹的結構掌握還不夠深，為了降低大家的學習成本，此處手動創建一棵簡單的二叉樹，以便快速進入二叉樹的操作學習。等二叉樹結構了解的差不多時，我們反過頭再來研究二叉樹真正的創建方式。

一.二叉樹鏈式結構的概念

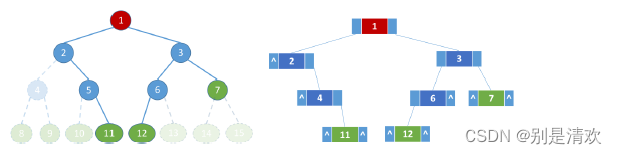
對于任意的二叉樹來說，每個結點只有一個雙親結點(根除外)，最多有兩個孩子。可以設計每個結點至少包括三個域：數據域data，左孩子域left和右孩子域right。其中，left域指向該結點的左孩子，data域記錄該結點的信息，right域指向該結點的右孩子。此結點結構形成的二叉樹稱為二叉鏈表。

二.二叉樹鏈式結構的功能實現

若有n個結點，則有2n個指針域，而除了根結點每個結點頭上都會連一個指針，故n個結點的二叉鏈表共有n+1個空鏈域。

2.1.鏈式二叉樹的定義

typedef int BTDataType;typedef struct BinaryTreeNode
{struct BinaryTreeNode* left;//左孩子指針struct BinaryTreeNode* right;//右孩子指針BTDataType data;//數據域
}BTNode;

2.2.鏈式二叉樹的構建

//創建結點
BTNode* BuyNode(BTDataType x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));assert(node);node->data = x;node->left = NULL;node->right = NULL;return node;
}//構造二叉樹
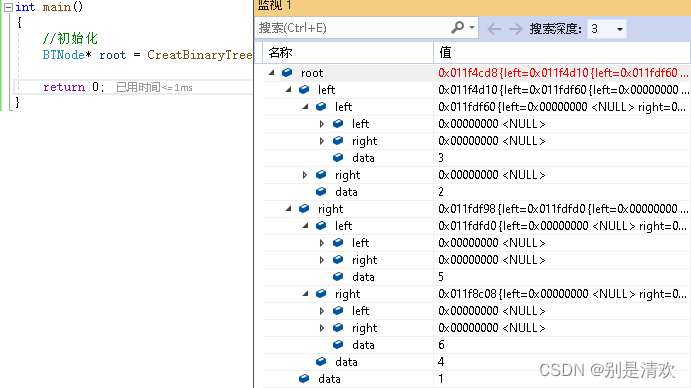
BTNode* CreatBinaryTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;
}

調試分析：

運行結果：

注意：

這種方式可以很簡單地找到指定結點的左右孩子，但是要找到指定結點的父結點就只能從根結點開始遍歷尋找。

2.3.鏈式二叉樹的遍歷

二叉樹的遍歷是指按一定規律對二叉樹中的每個結點進行訪問且僅訪問一次。二叉樹是非線性數據結構，通過遍歷可以將二叉樹中的結點訪問一次且僅一次，從而得到訪問結點的順序序列。從這個意義上說，遍歷操作就是將二叉樹中結點按一定規律線性化的操作，目的在于將非線性化結構變成線性化的訪問序列。

用L,D,R分別表示遍歷左子樹，訪問根結點，遍歷右子樹。如果規定按先左后右的順序，根據對根的訪問先后順序的不同，可以將DLR稱為先序遍歷或先根遍歷，將LDR稱為中序遍歷，將LRD稱為后序遍歷。

注意：先序，中序和后序遍歷都是遞歸定義的，即在其子樹中亦按上述規律進行遍歷。

案例分析：

2.3.1.先序遍歷

若二叉樹為空，則什么也不做；否則依次執行如下三個操作：

  1. 訪問根結點；
  2. 先序遍歷左子樹；
  3. 先序遍歷右子樹。?

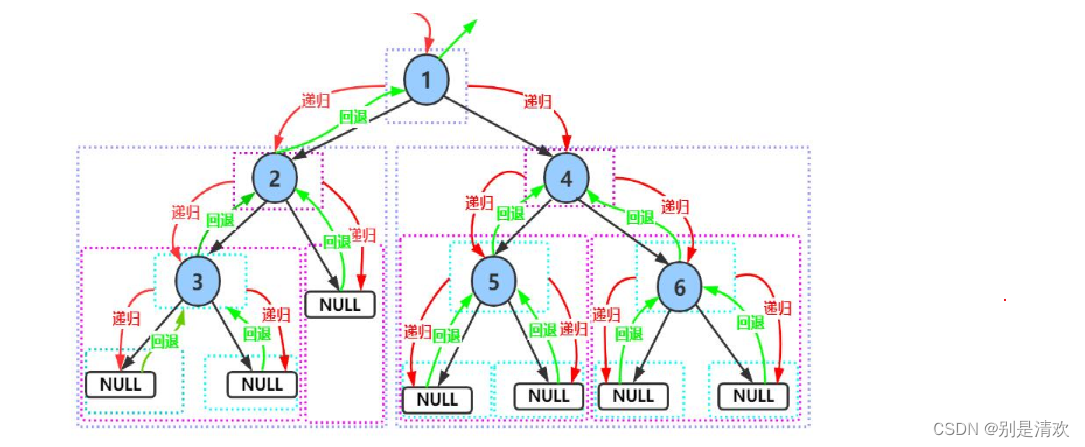
實現：

void PreOrder(BTNode* root)
{//若樹為空，則退出if (root == NULL){printf("# ");//若結點為空，則用#表示return;}//先訪問根結點printf("%d ", root->data);//然后訪問左子樹PreOrder(root->left);//再訪問右子樹PreOrder(root->right);
}

運行結果：

遞歸分析：

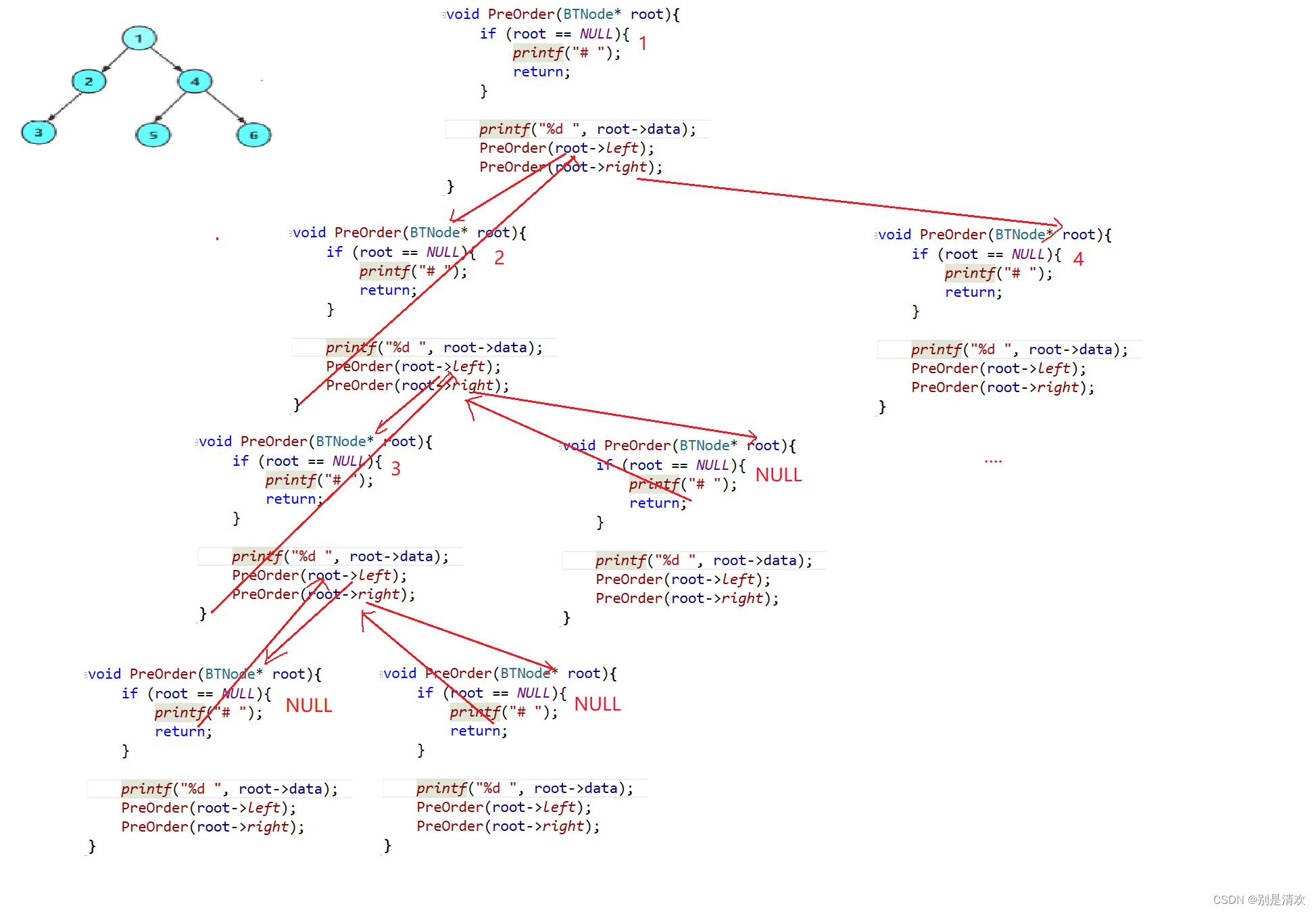
2.3.2.中序遍歷

若二叉樹為空，則什么也不做；否則依次執行如下三個操作：

  1. 中序遍歷左子樹；
  2. 訪問根結點；
  3. 中序遍歷右子樹。

實現：

void InOrder(BTNode* root)
{//若樹為空，則退出if (root == NULL){printf("# ");//若結點為空，則用#表示return;}//先訪問左子樹InOrder(root->left);//然后訪問根結點printf("%d ",root->data);//再訪問右子樹InOrder(root->right);
}

運行結果：

遞歸分析：

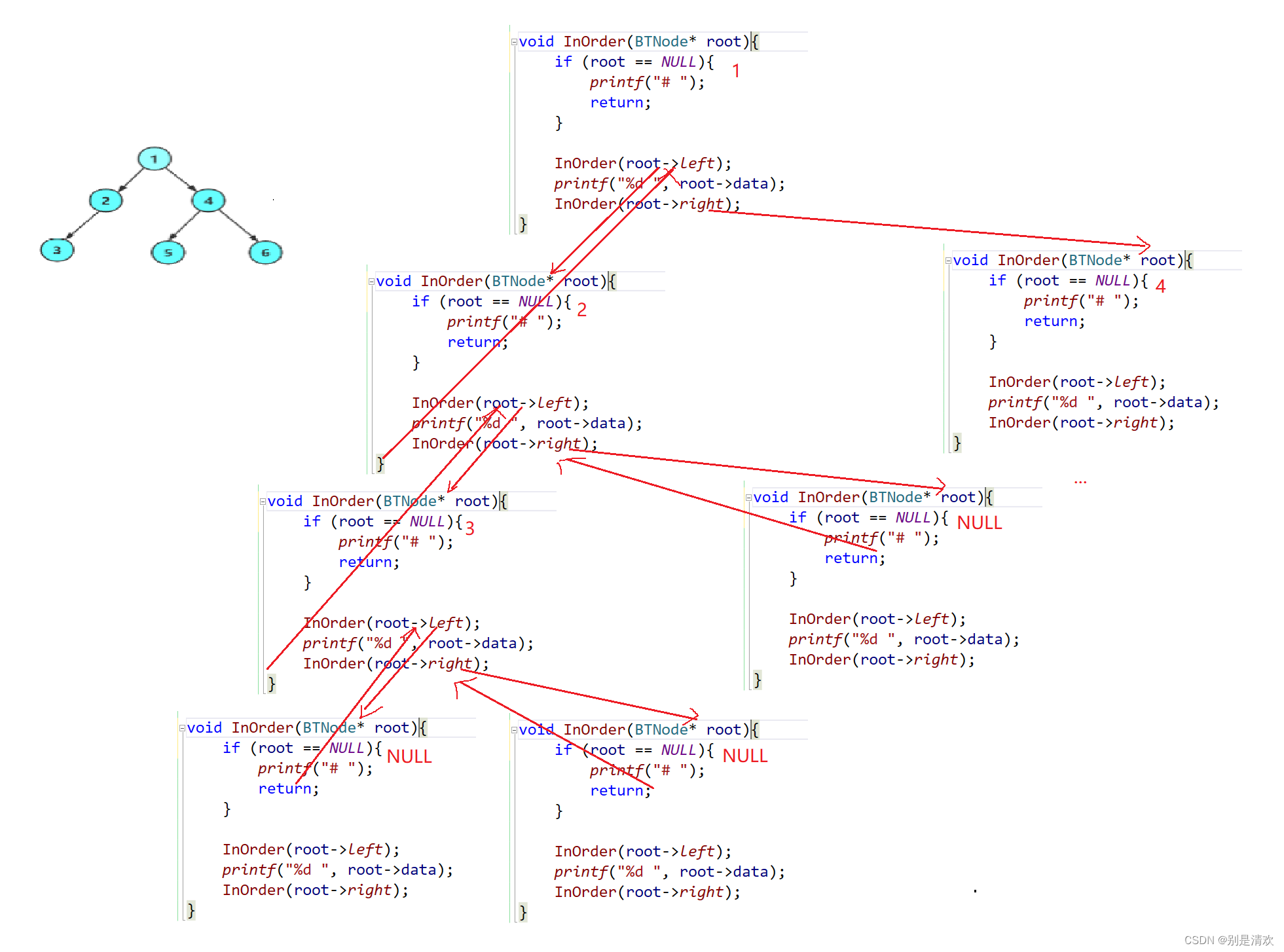
2.3.3.后序遍歷

若二叉樹為空，則什么也不做；否則依次執行如下三個操作：

  1. 后序遍歷左子樹；
  2. 后續遍歷右子樹；
  3. 訪問根結點。

實現：

void PostOrder(BTNode* root)
{//若樹為空，則退出if (root == NULL){printf("# ");//若結點為空，則用#表示return;}//先訪問左子樹PostOrder(root->left);//然后訪問右子樹PostOrder(root->right);//再訪問根結點printf("%d ", root->data);
}

運行結果：

小結：

遞歸算法的時間復雜度分析：設二叉樹有n個結點，對每個結點都要進行一次入棧和出棧的操作，即入棧和出棧各執行n次，對結點的訪問也是n次。這些二叉樹遞歸遍歷算法的時間復雜度為0(n)。

2.3.4.層序遍歷

設二叉樹的根結點所在層數為1，層序遍歷就是從所在二叉樹的根結點出發，首先訪問第一層的樹的根結點，然后從左到右訪問第二層的結點，接著是第三層的結點，以此類推，自上而下，自左至右逐層訪問樹的結點的過程就是層序遍歷。

實現方式：采用輔助隊列實現按層序遍歷二叉樹。

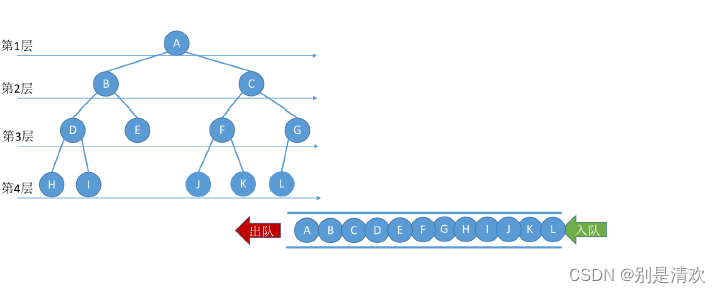
算法思想：

  1. 初始化一個輔助隊列；
  2. 根結點入隊；
  3. 若隊列非空，則隊頭結點出隊，訪問該結點，并將其左，右孩子插入隊尾(如果有的話)；
  4. 重復第三步直至隊列為空。

實現：

void LevelOrder(BTNode* root)
{//創建隊列并初始化Queue q;QueueInit(&q);//若根結點不為空，則先將根結點入隊if (root){//入隊QueuePush(&q, root);}//若隊列非空while (!QueueEmpty(&q)){//取隊頭元素BTNode* front = QueueFront(&q);//訪問隊頭結點printf("%d ",front->data);//出隊QueuePop(&q);//若左結點存在，則左結點入隊if (front->left){//入隊QueuePush(&q, front->left);}//若右節點存在，則右結點入隊if (front->right){//入隊QueuePush(&q, front->right);}}printf("\n");//銷毀隊列QueueDestory(&q);
}

運行結果：

2.4.鏈式二叉樹的求二叉樹的結點數量

法一：計數法

在遞歸調用過程中，局部變量和全局變量的傳遞方式可以類似的看成函數調用時的值傳遞和引用傳遞。

局部變量：類似于值傳遞過程中的形參和實參，可以看成是兩個完全不同的值，只是名字相同而已。每次遞歸調用時都會重新創建新的變量，它并不會覆蓋掉上次遞歸調用過程中創建的值。

全局變量：類似于傳地址過程中的形參和實參，可以看成是同一個變量。每次遞歸調用時并不會重新創建新的變量，在遞歸過程中對全局變量的修改，會影響到下一次遞歸調用過程中的值。

所以，我們在使用計數器進行結點個數統計是，要定義全局變量而非局部變量。

當使用局部變量時：

int TreeSize(BTNode* root)
{int count = 0;//若樹為空if (root == NULL){return;}//統計根結點++count;//統計左子樹TreeSize(root->left);//統計右子樹TreeSize(root->right);return count;
}

運行結果：

當使用全局變量時：

int count = 0;//不能定義一個局部變量，因為每次遞歸調用都會重新初始化為0void TreeSize(BTNode* root)
{//若樹為空if (root == NULL){return;}//統計根結點++count;//統計左子樹TreeSize(root->left);//統計右子樹TreeSize(root->right);}

運行結果：

這里存在一個問題：當我們多次打印輸出結果時，可以發現每次的輸出結果并不相同。如下所示：

為了避免該類問題的出現，只需在每次調用之前要將count進行初始化，防止下次調用時將前一次的調用結果進行累加。如下所示：

法二：分治法

使用計數法計算結點個數時存在較多需要注意的問題，而使用分治法可以有效解決此類問題。

采用遞歸算法，首先判斷樹是否為空樹，若為空樹，則返回0；若不是空樹，則將根結點root的左孩子結點和右孩子結點作為參數傳給函數TreeSize進行遞歸調用。

實現：

int TreeSize(BTNode* root)
{return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}

遞歸分析：

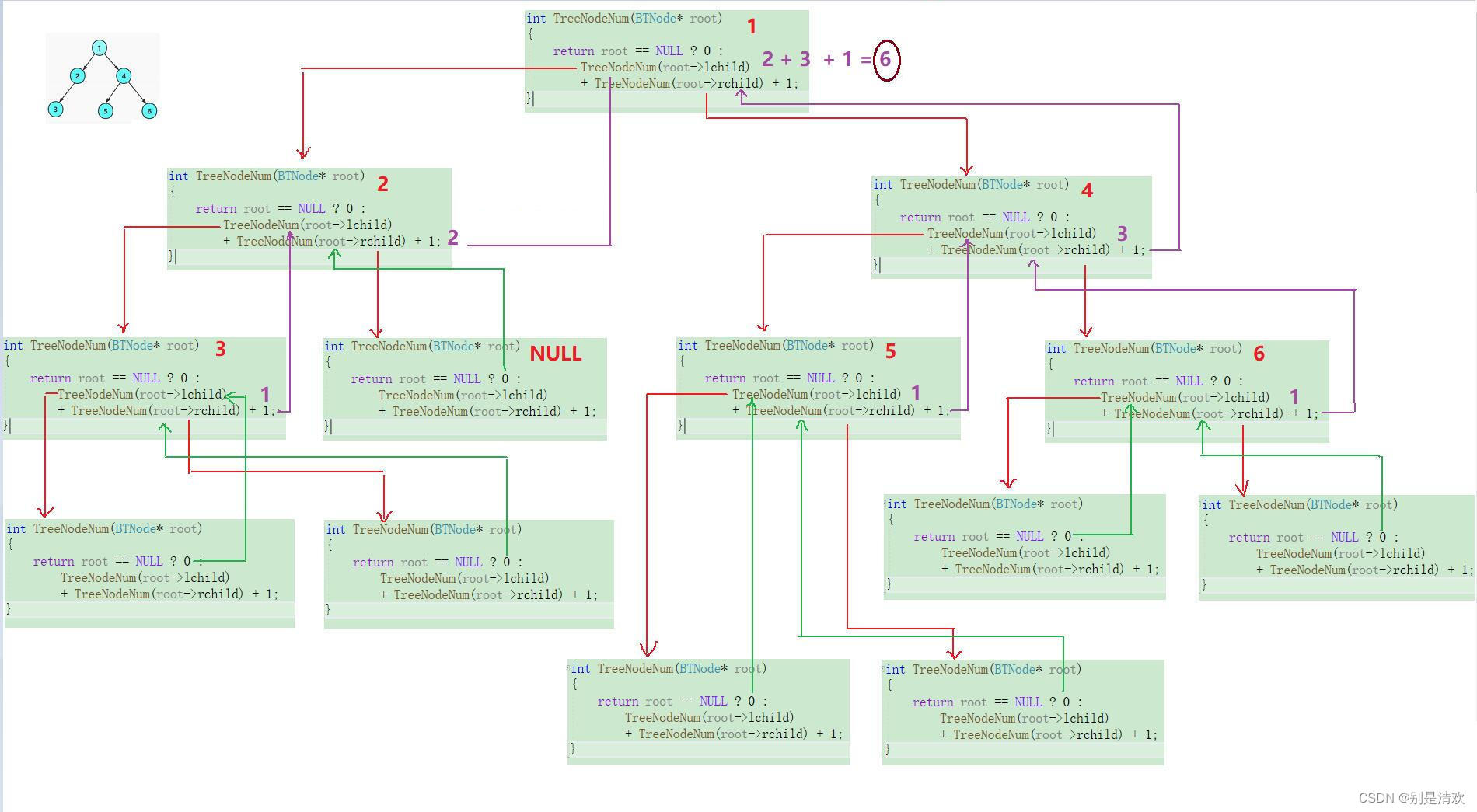
運行結果：

2.5.鏈式二叉樹的求二叉樹的葉子結點數量

采用遞歸算法，如果是空樹，返回0；如果只有一個結點，返回1；否則為左右子樹的葉子結點數之和。

實現：

int TreeLeafSize(BTNode* root)
{//若樹為空if (root == NULL){return 0;}//若為單獨的葉子，即只含一個結點if (root->left == NULL && root->right == NULL) {return 1;}//若樹不為空，也不為單獨的葉子return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

運行結果：

2.6.鏈式二叉樹的求二叉樹第k層結點的數量

采用遞歸算法，首先判斷k的取值是否合法，k的取值不能小于1，然后判斷樹是否為空，如果是空樹，則返回0；如果樹不為空，且k的值為1，則返回1；否則為左右子樹的第k-1層的結點數之和。

實現：

int TreeKLevel(BTNode* root, int k)
{//檢查k的范圍assert(k >= 1);//若樹為空if (root == NULL){return 0;}//若樹不為空，且k等于1，也就是根結點所在層次if (k == 1){return 1;}//求左子樹和右子樹的第k-1層的結點數之和return TreeKLevel(root->left, k - 1) + TreeKLevel(root->right, k - 1);
}

遞歸分析：

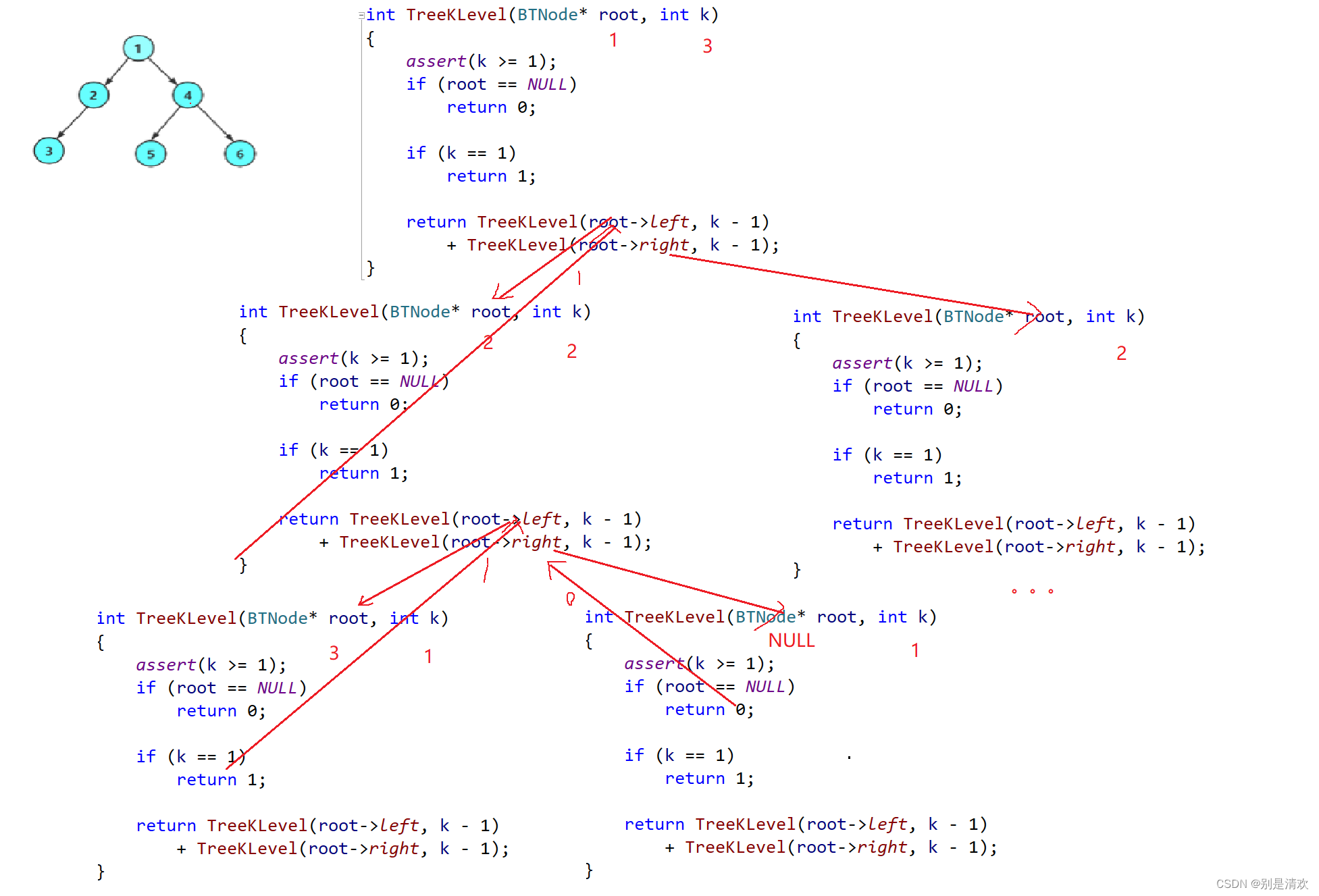
運行結果：

2.7.鏈式二叉樹的求二叉樹的高度

采用遞歸算法，首先判斷樹是否為空，若為空，則返回0；若不為空，則遞歸求左子樹的高度和右子樹的高度，然后再求出左子樹和右子樹高度的較大值，最后再將高度的最大值+1，即為所求二叉樹的高度。

實現：

int TreeDepth(BTNode* root)
{//若樹為空if (root == NULL){return 0;}//求左樹的高度int leftDepth = TreeDepth(root->left);//求右樹的高度int rightDepth = TreeDepth(root->right);//求兩者中較大值return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}

運行結果：

2.8.鏈式二叉樹的查找二叉樹中值為x的結點

采用遞歸算法，首先判斷樹是否為空，若樹為空，則返回NULL。當樹不為空，且根結點為所要查找的結點時，則返回根結點。否則，遞歸遍歷左子樹和右子樹。

實現：

BTNode* TreeFind(BTNode* root, BTDataType x)
{//若樹為空if (root == NULL){return NULL;}//若根結點為所要查找的結點if (root->data == x){return root;}//查找左子樹BTNode* ret1 = TreeFind(root->left, x);//若返回值不為空if (ret1){return ret1;}//查找右子樹BTNode* ret2 = TreeFind(root->right, x);//若返回值不為空if (ret2){return ret2;}return NULL;
}

遞歸分析：

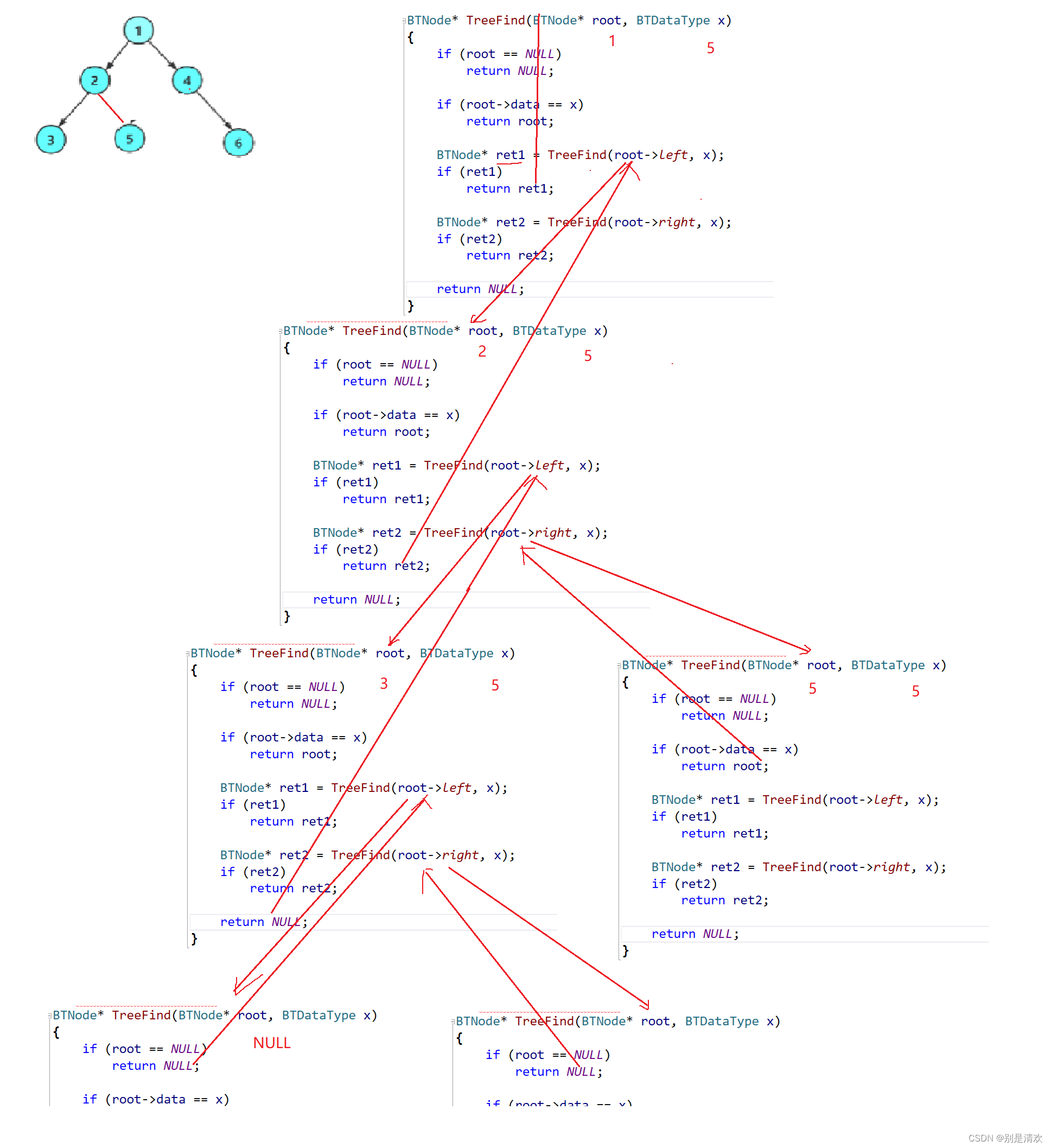
運行結果：

2.9.鏈式二叉樹的判斷二叉樹是否是完全二叉樹

完全二叉樹：對于一棵深度為h的二叉樹，其前h-1層結點個數均達到最大值，第h層結點個數可能沒有達到最大值，但從左到右是連續的。

算法思想：

  1. 初始化一個輔助隊列；
  2. 根結點入隊；
  3. 若隊列非空，則隊頭結點出隊，訪問該結點，并將其左，右孩子插入隊尾(包含空結點)；
  4. 重復第三步直至遇到空結點，并查看其后續是否有非空結點。若有，則該二叉樹不是完全二叉樹；若沒有，則該二叉樹是完全二叉樹。

實現：

int TreeComplete(BTNode* root)
{//初始化隊列Queue q;QueueInit(&q);//先將根結點入隊if (root){QueuePush(&q, root);}while (!QueueEmpty(&q)){//讀取隊頭元素并出隊BTNode* front = QueueFront(&q);QueuePop(&q);//若隊頭結點非空if (front){//左結點入隊，包含空結點QueuePush(&q, front->left);//右結點入隊，包含空結點QueuePush(&q, front->right);}else{//遇到空，則跳出層序遍歷break;}}//1.如果空后面全是空結點，則是完全二叉樹//2.如果空后面還有非空結點，則不是完全二叉樹while (!QueueEmpty(&q)){//讀取隊頭元素并出隊BTNode* front = QueueFront(&q);QueuePop(&q);//front存放的是樹的結點的指針if (front){QueueDestory(&q);return false;}}//銷毀QueueDestory(&q);return true;
}

運行結果：

2.10.鏈式二叉樹的二叉樹的銷毀

采用遞歸算法，首先判斷樹是否為空，若為空，則返回NULL。若樹不為空，則先遞歸銷毀左子樹，然后再銷毀右子樹，最后再釋放根結點。

實現：

void TreeDestroy(BTNode* root)
{//若樹為空if (root == NULL){return;}//銷毀左子樹TreeDestroy(root->left);//銷毀右子樹TreeDestroy(root->right);printf("%p:%d\n", root, root->data);//釋放根結點free(root);
}

運行結果：

三.二叉樹基礎OJ練習

題一：單值二叉樹

題目描述：

如果二叉樹每個結點都具有相同的值，那么該二叉樹就是單值二叉樹。只有給定的樹是單值二叉樹，才返回true；否則返回false。

法一：標記法

設置標志位flag進行單值二叉樹的判斷。若樹為空或者標志位flag為flase，則直接返回；若根結點的值不等于val，則將標志位flag設為flase，同時返回；若上述兩個條件均滿足，則遞歸遍歷左子樹和右子樹。

實現：

struct TreeNode
{int val;struct TreeNode* left;struct TreeNode* right;
};//法一：設置標記位
bool flag = true;
void PreOrderCompare(struct TreeNode* root, int val)
{//若樹為空if (root == NULL || flag == false)//flag==flase：若左子樹不滿足條件則直接退出，以免對右子樹進行不必要的遞歸遍歷{return;}//如果根結點的值不等于val，則直接退出，不用往下遞歸if (root->val != val){flag = false;return;}//比較左子樹PreOrderCompare(root->left, val);//比較右子樹PreOrderCompare(root->right,val);
}bool isUnivalTree(struct TreeNode* root)
{//若樹為空if (root == NULL){return true;}flag = true;PreOrderCompare(root, root->val);return flag;
}

法二：

首先判斷根結點root是否為NULL，若為空則直接返回true。然后判斷根結點root的左孩子與右孩子是否為空且其值與root的值是否相同，若不同，則返回false；若相同，則直接遞歸遍歷root的左子樹和右子樹，判斷其否為單值二叉樹。

實現：

struct TreeNode
{int val;struct TreeNode* left;struct TreeNode* right;
};bool isUnivalTree(struct TreeNode* root)
{//如果樹為空if (root == NULL){return true;}//若左孩子不為空且左孩子的值不等于根結點if (root->left && root->left->val != root->val){return false;}//若右孩子不為空且右孩子的值不等于根結點if (root->right && root->right->val != root->val){return false;}//遞歸遍歷左子樹和右子樹return isUnivalTree(root->left) && isUnivalTree(root->right);//遞歸調用的返回，都是返回到遞歸調用的上一層
}

遞歸分析：

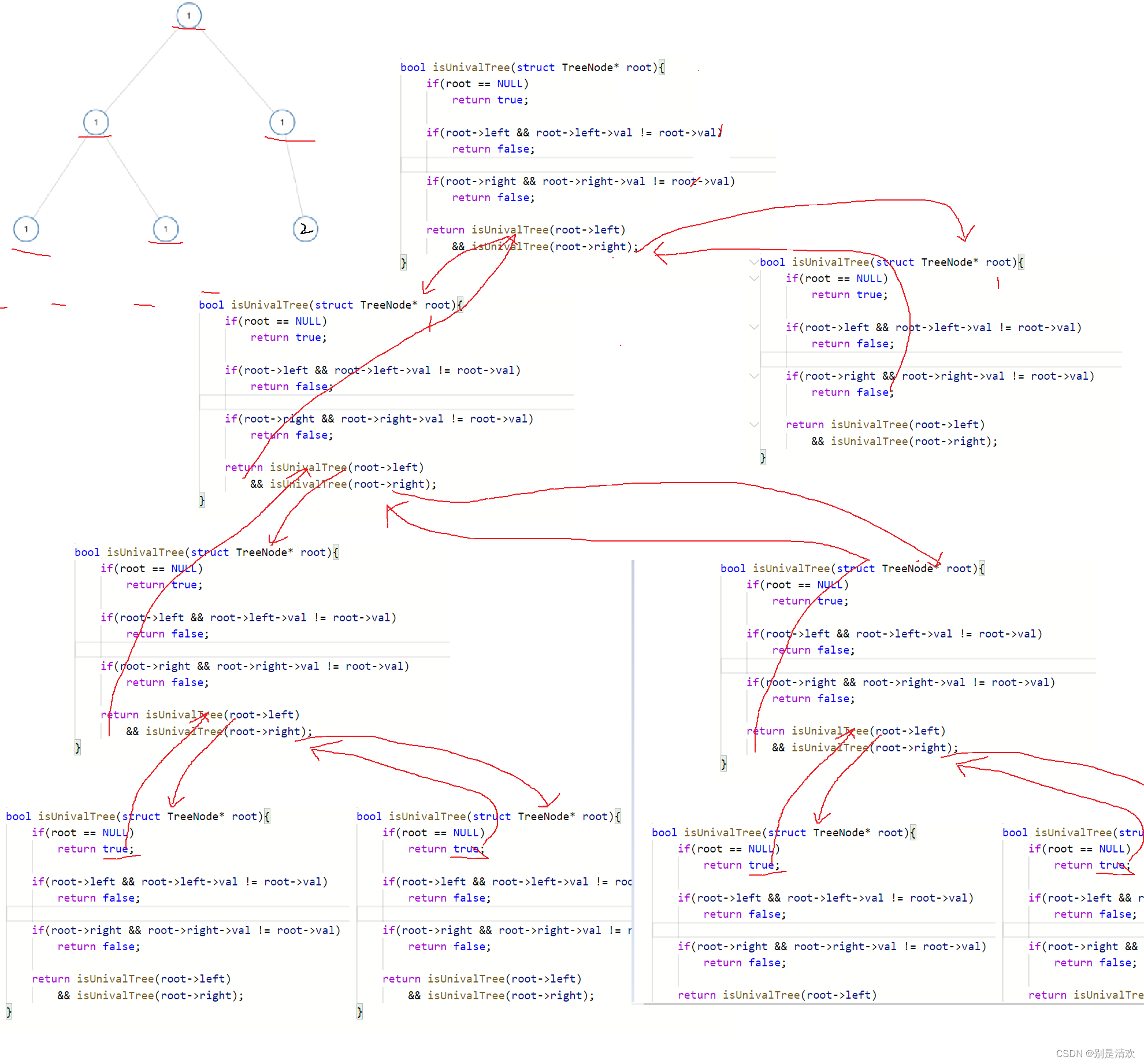
題二：相同的樹

題目描述：

給你兩棵二叉樹的根結點p和q，編寫一個函數來檢驗這兩棵樹是否相同。如果兩棵樹在結構上相同，并且結點具有相同的值，則認為它們是相同的。

分析：

首先判斷兩棵樹是否均為空，若均為空，則返回true；若有一棵樹為空，則返回false。然后在兩棵樹均不為空的情況下，判斷其對應的根結點的值是否相等，若不相等則返回false。最后再遞歸遍歷兩棵樹對應的左子樹和右子樹，判斷其對應的結點值是否相等。

實現：

struct TreeNode
{int val;struct TreeNode* left;struct TreeNode* right;
};bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{//如果兩棵樹都為空if (p == NULL && q == NULL){return true;}//如果兩棵樹有一棵為空if (p == NULL || q == NULL){return false;}//如果兩棵子樹都不為空，且兩個根結點的值不相等if (p->val != q->val){return false;}return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}

題三：對稱二叉樹

題目描述：

給你一個二叉樹的根結點root，檢查它是否軸對稱。

分析：

首先判斷樹是否為空，若為空則返回true，若不唯空，則判斷根結點root對應的左子樹和右子樹。然后轉為對左子樹和右子樹的判斷，若兩棵子樹均為空，咋返回true；若有一棵子樹為空，則返回false；若兩棵子樹均不為空，且其對應的根結點的值不相等，則返回false。最后再遞歸遍歷，判斷左子樹的左子樹與右子樹的右子樹以及左子樹的右子樹與右子樹的左子樹是否相等。

實現：

struct TreeNode
{int val;struct TreeNode* left;struct TreeNode* right;
};bool isSymmetricSubTree(struct TreeNode* root1, struct TreeNode* root2)
{//若兩棵樹均為空if (root1 == NULL && root2 == NULL){return true;}//若有一棵樹為空if (root1 == NULL || root2 == NULL){return false;}//若兩棵樹均不為空if (root1->val != root2->val){return false;}return isSymmetricSubTree(root1->left, root2->right) && isSymmetricSubTree(root1->right, root2->left);
}bool isSymmetric(struct TreeNode* root)
{//若樹為空if (root == NULL){return true;}//若樹不為空return isSymmetricSubTree(root->left, root->right);
}

題四：另一棵樹的子樹

題目描述：

給你兩棵二叉樹root和subRoot。檢驗root中是否包含和subRoot具有相同結構和節點值的子樹。如果存在，返回true；否則，返回false。
二叉樹tree的一棵子樹包括tree的某個節點和這個節點的所有后代節點。tree也可以看做它自身的一棵子樹。

分析：

遍歷二叉樹root中的每一個結點，然后將每一個結點都作為根結點并與subRoot的根結點進行比較，若對應的根結點值相同，則調用函數isSameTree進行左右子樹的比較。如果左右子樹均相同，則subRoot是root的子樹；否則繼續將二叉樹root的下一個結點與subRoot的根結點進行比較。重復上述操作，直至找到一棵子樹與二叉樹subRoot相同或者二叉樹root的所有子樹均與subRoot不同并退出。

實現：

struct TreeNode
{int val;struct TreeNode* left;struct TreeNode* right;
};bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{//如果兩棵樹都為空if (p == NULL && q == NULL){return true;}//如果兩棵樹有一棵為空if (p == NULL || q == NULL){return false;}//如果兩棵子樹都不為空，且兩個根結點的值不相等if (p->val != q->val){return false;}return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot)
{//若樹為空if (root == NULL)return false;//若樹不為空if (isSameTree(root, subRoot)){return true;}//將原樹中所有子樹都找出來，然后跟subRoot比較return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}

遞歸分析：

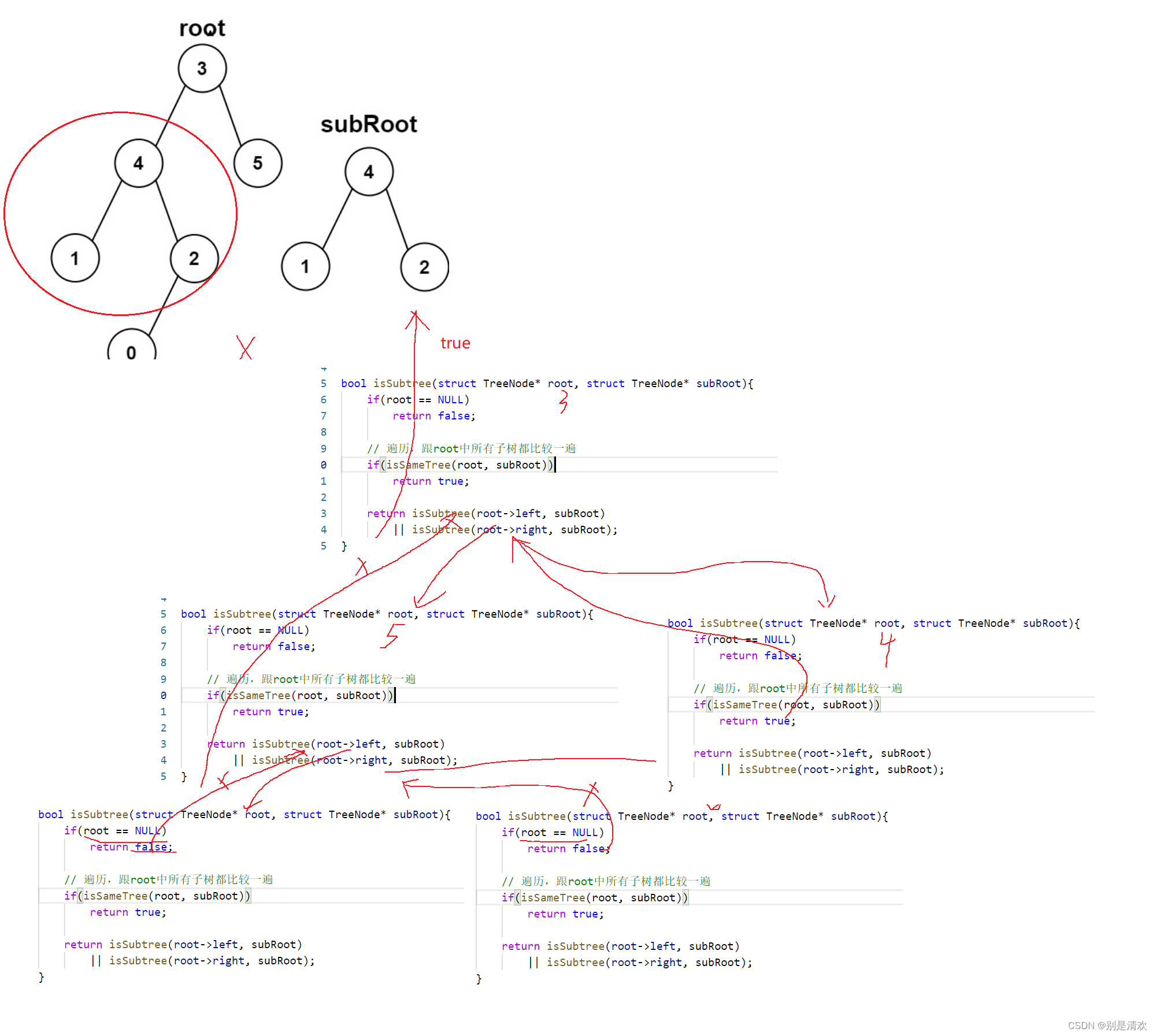
題五：二叉樹的前序遍歷

題目描述：

給你二叉樹的根結點root，返回它結點值的前序遍歷。

分析：

實現函數TreeSize，用以統計二叉樹中的結點個數并返回給returnSize。同時開辟好returnSize個int 類型大小的數組空間，用于存放遍歷后的各個結點。最后再調用函數preorder進行先序遍歷，并返回數組首元素的地址。

實現：

struct TreeNode
{int val;struct TreeNode* left;struct TreeNode* right;
};//求二叉樹的結點個數
int TreeSize(struct TreeNode* root)
{return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}//前序遍歷，并將遍歷后的結點值存入數組中
void preorder(struct TreeNode* root, int* a, int* pi)//pi的值要加引用，否則形參的修改不會影響實參
{//如果樹為空if (root == NULL){return;}//若樹不為空a[(*pi)++] = root->val;//遍歷左子樹preorder(root->left, a, pi);//遍歷右子樹preorder(root->right, a, pi);
}int* preorderTraversal(struct TreeNode* root, int* returnSize)
{//*returnSize用于接收二叉樹的節點個數*returnSize = TreeSize(root);//開辟*returnSize個int類型大小的空間用于存放遍歷后的結點int* a = (int*)malloc(*returnSize * sizeof(int));//進行前序遍歷int i = 0;preorder(root, a, &i);return a;
}

題六：二叉樹遍歷

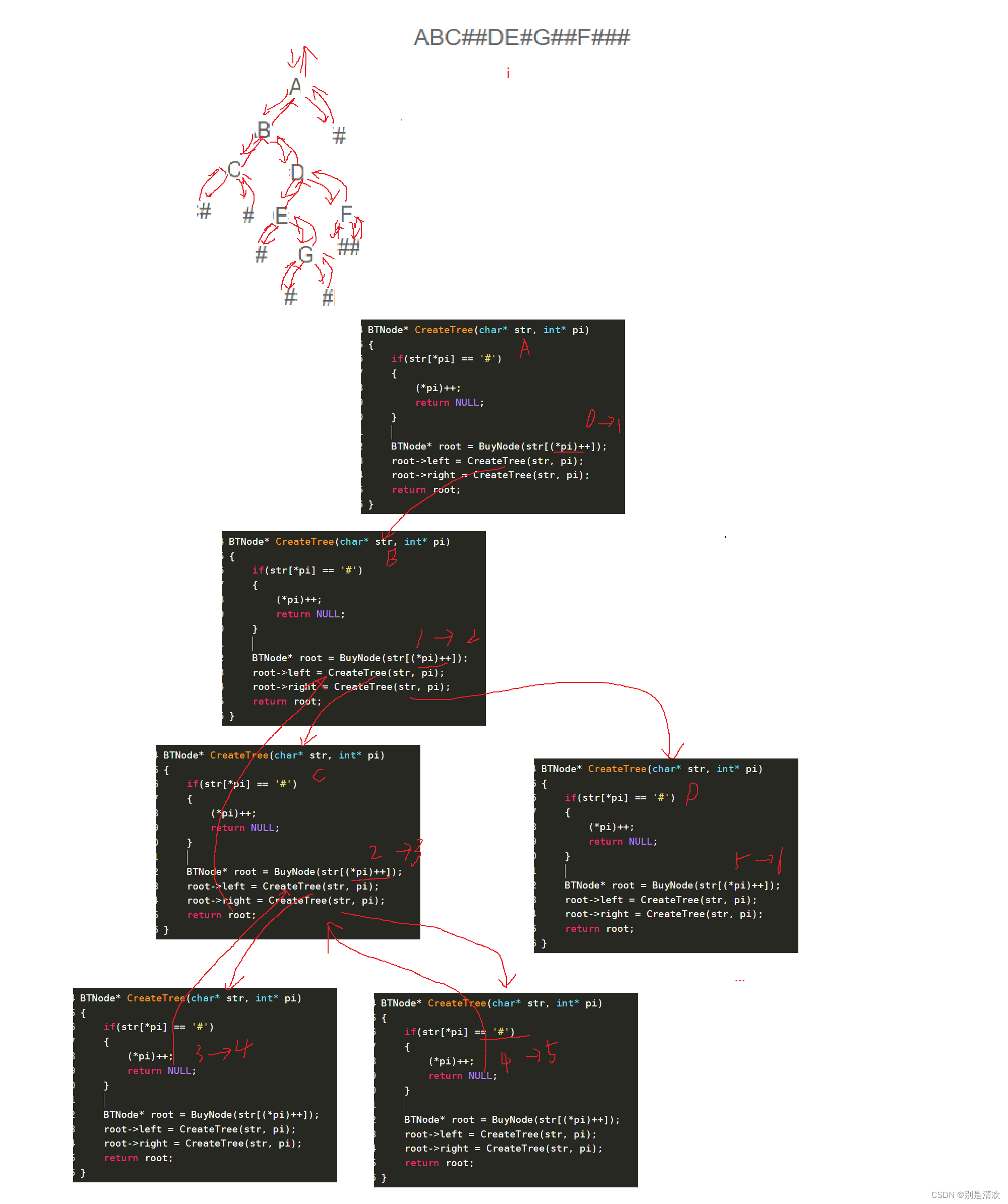
題目描述：

編一個程序，讀入用戶輸入的一串先序遍歷字符串，根據此字符串建立一個二叉樹（以指針方式存儲）。例如如下的先序遍歷字符串：ABC##DE#G##F###其中"#"表示的是空格，空格字符代表空樹。建立起此二叉樹以后，再對二叉樹進行中序遍歷，輸出遍歷結果。

分析：

根據所給的先序遍歷字符串，采用前序遍歷的方式進行二叉樹的創建，再將創建好的二叉樹進行中序遍歷即可。

實現：

//二叉樹的定義
typedef char BTDataType;
typedef struct BinaryTreeNode
{struct BinaryTreeNode* left;//左子樹struct BinaryTreeNode* right;//右子樹BTDataType data;
}BTNode;//創建結點
BTNode* BuyNode(BTDataType x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));assert(node);node->data = x;node->left = NULL;node->right = NULL;return node;
}//前序創建二叉樹
BTNode* CreateTree(char* str, int* pi)
{//若結點為空，也就是空樹，空樹數組的下標也要++，且為它malloc空間進行存儲if (str[*pi] == '#'){(*pi)++;return NULL;}//前序構建二叉樹BTNode* root = BuyNode(str[(*pi)++]);root->left = CreateTree(str, pi);root->right = CreateTree(str, pi);return root;
}//中序遍歷二叉樹
void InOrder(BTNode* root)
{//判斷樹是否為空if (root == NULL){return;}InOrder(root->left);printf("%c ",root->data);InOrder(root->right);
}int main()
{char str[100];scanf("%s", str);int i = 0;BTNode* root = CreateTree(str, &i);InOrder(root);return 0;
}

遞歸分析：

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/37695.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/37695.shtml
英文地址，請注明出處：http://en.pswp.cn/news/37695.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

Linux知識點 -- 進程概念（補充）

Linux知識點 -- 進程概念（補充）

Linux知識點 – 進程概念（補充） 文章目錄 Linux知識點 -- 進程概念（補充）一、進程地址空間的堆區二、虛擬地址到物理地址之間的轉化三、虛擬地址到物理地址之間的映射 一、進程地址空間的堆區 在用戶每次使用malloc等函數在進程的…
閱讀更多...
OBD接口引腳定義

OBD接口引腳定義

汽車的OBD接口引腳定義分配如下圖所示，OBD接口共有16個引腳（可參考 ISO 15031-3）。 1、引腳1,3,8,9,11,12,13 引腳1,3,8,9,11,12,13由主機廠進行分配。 2、引腳2 如果車輛中使用SAE J1850 10,4 VPW（可變脈沖）來提供…
閱讀更多...
【React】精選10題

【React】精選10題

1.React Hooks帶來了什么便利？ React Hooks是React16.8版本中引入的新特性，它帶來了許多便利。 更簡單的狀態管理 使用useState Hook可以在函數組件中方便地管理狀態，避免了使用類組件時需要繼承React.Component的繁瑣操作。 避免使用類組件…
閱讀更多...
小紅書運營 變現方法總結（精）

小紅書運營 變現方法總結（精）

大家好，我是網媒智星，今天跟大家分享一下小紅書運營方面的知識，怎樣利用小紅書變現？全篇傾情干貨輸出，認真學習，保證您收獲多多。 首先，讓我們來分析一下小紅書平臺的優勢。關于賣東西&#xff…
閱讀更多...
Open3D (C++) 基于擬合高差的點云地面點提取

Open3D (C++) 基于擬合高差的點云地面點提取

目錄 一、算法原理1、原理概述2、參考文獻二、代碼實現三、結果展示1、原始點云2、提取結果四、相關鏈接系列文章（連載中。。。）： Open3D (C++) 基于高程的點云地面點提取Open3D (C++) 基于擬合平面的點云地面點提取Open3D (C++) 基于擬合高差的點云地面點提取</
閱讀更多...
vue + less 實現動態主題換膚功能

vue + less 實現動態主題換膚功能

文章目錄 前言一、前提條件1. 初始化vue項目2. 安裝插件 二、新建文件夾主題theme1.style.less文件2.model.js文件3.theme.js文件theme文件夾最終效果 三、修改vue.config.js文件四、頁面上的具體使用1. index.vue 頁面2. index.vue 頁面注意點說明3. index.vue 效果 五、在js中…
閱讀更多...
VSCode使用SSH無密碼連接Ubuntu

VSCode使用SSH無密碼連接Ubuntu

VSCode使用SSH無密碼連接Ubuntu 前提條件&#xff1a; 1. 能夠正常使用vscode的Remote-ssh連接Ubuntu 2. Ubuntu配置靜態ip&#xff08;否則經常需要修改Remote-ssh的配置文件里的IP&#xff09; 鏈接-> ubuntun 18.04設為靜態ip&#xff08;.net模式&#xff0c;可連接…
閱讀更多...
shell使用總結

shell使用總結

一、語法 數據類型 字符串 如果沒有特殊說明&#xff0c;數據類型默認都是字符串。常見字符串操作有&#xff1a; 已知變量strabcabc 1、切片 echo ${str:1:3} #${varName:offset:size},分頁取子串 echo ${str:2} #${varName:offset},偏移offset個字符取至末端 echo …
閱讀更多...
加載AB包程序集，反射獲取并實例化類調用方法

加載AB包程序集，反射獲取并實例化類調用方法

加載AB包文件&#xff0c;加載bytes程序集資源&#xff0c;通過反射獲取類&#xff0c;實例化添加組件&#xff0c;調用方法 public class LoadAB : MonoBehaviour {private void Update(){if (Input.GetKeyDown(KeyCode.H)){Load();}}void Load(){string classname "ID…
閱讀更多...
如何解決docker中出現的“bash: vim: command not found”

如何解決docker中出現的“bash: vim: command not found”

目錄 問題描述&#xff1a; 問題解決&#xff1a; 問題描述&#xff1a; 在docker中&#xff0c;想要執行vim編輯文件&#xff0c;彈出“docker bash: vim: command not found“&#xff08;如下圖&#xff09;&#xff0c;請問該如何解決&#xff1f; 問題解決&#xff1a; …
閱讀更多...
FPGA應用學習筆記------系統復位一（同異復位）

FPGA應用學習筆記------系統復位一（同異復位）

要滿足復位恢復時間才能正常復位&#xff0c;不然會產生輸出準穩態&#xff0c;輸出邏輯錯誤 復位恢復時間只會存在復位釋放時刻&#xff0c;不會出現在確立時刻&#xff0c;則不推薦完全異步復位 完全同步復位&#xff0c;肯定是同步于時鐘滴&#xff0c;并將總是滿足時鐘條件…
閱讀更多...
研發工程師玩轉Kubernetes——就緒探針（Readiness Probe）和服務（Service）

研發工程師玩轉Kubernetes——就緒探針（Readiness Probe）和服務（Service）

在《研發工程師玩轉Kubernetes——啟動、存活和就緒探針》中&#xff0c;我們講了就緒探針和服務之間的特殊關系。就緒探針檢測失敗并不代表整個程序處于“非存活”狀態&#xff0c;可能只是短暫臨時的不可以提供服務&#xff0c;比如CPU階段性占滿&#xff0c;導致就緒探針檢測…
閱讀更多...
【Spring MVC】Spring MVC基于注解的程序開發

【Spring MVC】Spring MVC基于注解的程序開發

目錄 一、什么是Spring MVC 二、Spring MVC項目的創建和使用 1、實現客戶端和服務器端之間的連接 1.1、RequsestMapping注解 1.2、RequestMapper的簡單使用 1.3、使用GetMapping和POSTMapping注解來實現HTTP連接 三、獲取參數 1、實現獲取單個參數 2、實現獲取對象 3…
閱讀更多...
解決ubantu驅動掉了的問題

解決ubantu驅動掉了的問題

這里寫自定義目錄標題 解決ubuntu驅動掉了的問題 解決ubuntu驅動掉了的問題 首先確定是否有驅動&#xff1a; ls /usr/src | grep nvidia若有&#xff0c;則大概率是驅動版本與內核版本對應不上&#xff0c;則把內核版本切換為初始版本即可。參照&#xff1a;https://blog.cs…
閱讀更多...
書寫自動智慧：探索Python文本分類器的開發與應用：支持二分類、多分類、多標簽分類、多層級分類和Kmeans聚類

書寫自動智慧：探索Python文本分類器的開發與應用：支持二分類、多分類、多標簽分類、多層級分類和Kmeans聚類

書寫自動智慧&#xff1a;探索Python文本分類器的開發與應用&#xff1a;支持二分類、多分類、多標簽分類、多層級分類和Kmeans聚類 文本分類器&#xff0c;提供多種文本分類和聚類算法&#xff0c;支持句子和文檔級的文本分類任務&#xff0c;支持二分類、多分類、多標簽分類…
閱讀更多...
nodejs+vue+elementui+express智慧社區小區物業管理系統的設計與實現_2p760

nodejs+vue+elementui+express智慧社區小區物業管理系統的設計與實現_2p760

開發語言 node.js 框架&#xff1a;Express 前端:Vue.js 數據庫&#xff1a;mysql 數據庫工具&#xff1a;Navicat 開發軟件&#xff1a;VScode 前端nodejsvueelementuiexpress vue的文件結構其實就是一個index.html 中間的內容&#xff0c;用的是vue&#xff0c;但最終都會轉…
閱讀更多...
OpenCV圖像處理——形態學操作

OpenCV圖像處理——形態學操作

目錄 連通性形態學操作腐蝕和膨脹開閉運算禮帽和黑帽 連通性 形態學操作 形態學轉換是基于圖像形狀的一些簡單操作。它通常在二進制圖像上執行。腐蝕和膨脹時兩個基本的形態學運算符。然后它的變體形式如開運算&#xff0c;閉運算&#xff0c;禮帽黑帽等 腐蝕和膨脹 cv.erode…
閱讀更多...
費曼學習法

費曼學習法

費曼學習法 費曼學習法&#xff08;Feynman Technique&#xff09;是一種學習和理解復雜概念的方法&#xff0c;以理查德費曼&#xff08;Richard Feynman&#xff09;這位著名的理論物理學家命名。該方法的核心思想是通過將學習內容簡化并用自己的話解釋給別人&#xff0c;來…
閱讀更多...
Node.js學習筆記-04

Node.js學習筆記-04

這第九章也是個大重點 九、玩轉進程 Node在選型時決定在V8引擎之上構建&#xff0c;也就意味著它的模型與瀏覽器類似。 本章關于進程的介紹和討論將會解決如下兩個問題&#xff1a; 單進程單線程并非完美&#xff0c;如今CPU基本均是多核的&#xff0c;真正的服務器&#xf…
閱讀更多...
背上小書包準備面試之TypeScript篇

背上小書包準備面試之TypeScript篇

目錄 typescript是啥&#xff1f;與javascript的區別&#xff1f; typescript數據類型&#xff1f; typescript中枚舉類型&#xff1f;應用場景&#xff1f; typescript中接口的理解&#xff1f;應用場景&#xff1f; typescript中泛型的理解&#xff1f;應用場景&#xf…
閱讀更多...
最新文章

Copyright @ 2022~2023