目錄
代碼
回歸問題的損失函數
分類問題的損失函數
1、 0-1損失 (zero-one loss)
2、Logistic loss
3、Hinge loss
4、指數損失(Exponential loss)
機器學習的損失函數
Cross Entropy Loss Function(交叉熵損失函數)
交叉熵優點
?Mean Squared Error (均方誤差)
均方差不足
實例
? 交叉熵求解損失:
?均方差函數求損失
學習過程
學習筆記
?參考文獻
代碼
損失函數的一般表示為L(y,f(x)),用以衡量真實值y和預測值f(x)之間不一致的程度,一般越小越好。為了便于不同損失函數的比較,常將其表示為單變量的函數,在回歸問題中這個變量為y?f(x),在分類問題中則為yf(x)。下面分別進行討論。
?
回歸問題的損失函數
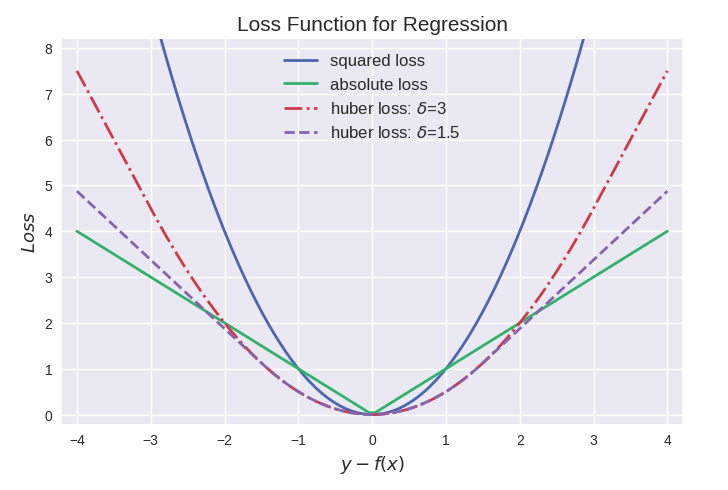
回歸問題中y和f(x)皆為實數∈R,因此用殘差 y?f(x)來度量二者的不一致程度。殘差 (的絕對值) 越大,則損失函數越大,學習出來的模型效果就越差(這里不考慮正則化問題)。
其中最常用的是平方損失,然而其缺點是對于異常點會施以較大的懲罰,因而不夠robust。如果有較多異常點,則絕對值損失表現較好,但絕對值損失的缺點是在y?f(x)=0處不連續可導,因而不容易優化。
Huber損失是對二者的綜合,當|y?f(x)|小于一個事先指定的值δ時,變為平方損失,大于δ時,則變成類似于絕對值損失,因此也是比較robust的損失函數。三者的圖形比較如下:
huber函數與smoothL1函數差不多
分類問題的損失函數
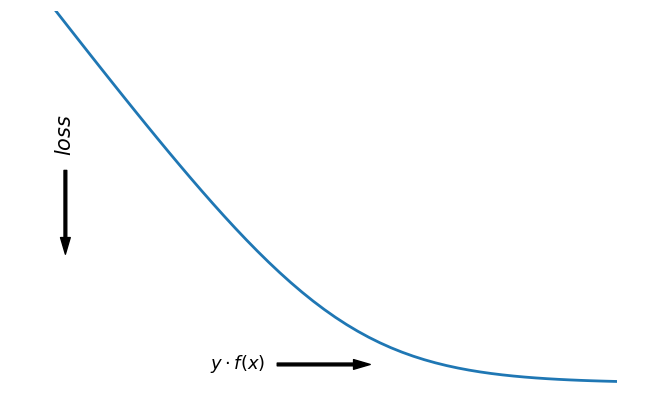
對于二分類問題,y∈{?1,+1}
,損失函數常表示為關于yf(x)
的單調遞減形式。如下圖:
?
yf(x)被稱為margin,其作用類似于回歸問題中的殘差 y?f(x)。
二分類問題中的分類規則通常為 sign(f(x))={+1ifyf(x)≥0?1ifyf(x)<0
可以看到如果 yf(x)>0,則樣本分類正確,yf(x)<0 則分類錯誤,而相應的分類決策邊界即為 f(x)=0
。所以最小化損失函數也可以看作是最大化 margin 的過程,任何合格的分類損失函數都應該對 margin<0 的樣本施以較大的懲罰。
1、 0-1損失 (zero-one loss)

0-1損失對每個錯分類點都施以相同的懲罰,這樣那些“錯的離譜“ (即 margin→?∞)的點并不會收到大的關注,這在直覺上不是很合適。另外0-1損失不連續、非凸,優化困難,因而常使用其他的代理損失函數進行優化。
2、Logistic loss

?
3、Hinge loss
hinge loss為svm中使用的損失函數,hinge loss使得yf(x)>1的樣本損失皆為0,由此帶來了稀疏解,使得svm僅通過少量的支持向量就能確定最終超平面。
hinge loss被翻譯為“合頁損失”,那么合頁究竟長啥樣?如圖,確實有點像hinge loss的形狀:

4、指數損失(Exponential loss)
exponential loss為AdaBoost中使用的損失函數,使用exponential loss能比較方便地利用加法模型推導出AdaBoost算法 (具體推導過程)。然而其和squared loss一樣,對異常點敏感,不夠robust。
最后來張全家福:
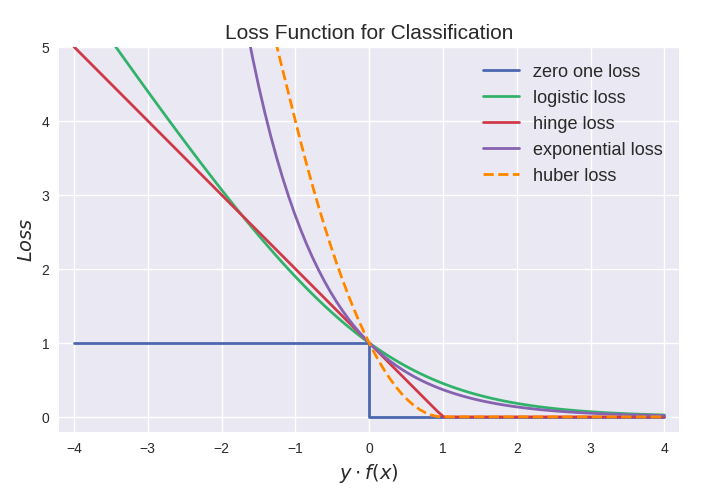
從上圖可以看出上面介紹的這些損失函數都可以看作是0-1損失的單調連續近似函數,而因為這些損失函數通常是凸的連續函數,因此常用來代替0-1損失進行優化。它們的相同點是都隨著margin→?∞
而加大懲罰;不同點在于,logistic loss和hinge loss都是線性增長,而exponential loss是以指數增長。
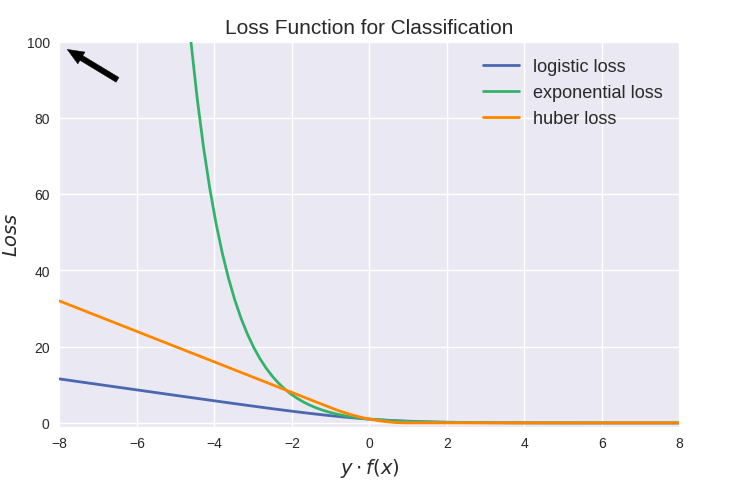
值得注意的是上圖中modified huber loss的走向和exponential loss差不多,并不能看出其robust的屬性。其實這和算法時間復雜度一樣,成倍放大了之后才能體現出巨大差異:
機器學習的損失函數
Cross Entropy Loss Function(交叉熵損失函數)


交叉熵優點

?Mean Squared Error (均方誤差)

均方差不足

實例

 交叉熵求解損失:
交叉熵求解損失:

?均方差函數求損失

學習過程


?4、根據損失函數進行梯度計算,反向傳播更新參數,反復1-4
學習筆記



?參考文獻
https://zhuanlan.zhihu.com/p/35709485
常見回歸和分類損失函數比較





)

o)

)





)



