目錄
一、機器學習概念
二、機器學習步驟
三、有監督學習
1、k-近鄰算法
核心思想
實例:手寫數字的識別
優缺點:
2、決策樹
相關概念
核心思想
一些小技巧
優缺點
3、神經網絡
4、SVM——支持向量機
核心思想
SVM和SVR的區別
? 優缺點
?5、集成學習或元算法
核心思想
常見的元算法或者集成學習——串行bagging(隨機森林等)、并行boosting(自適應boosting--adaboosting等)
0)串行訓練與并行訓練
1)bagging(自舉匯聚法)——基于數據隨機重抽樣的分類器構建
2)boosting——基于錯誤提升分類器的性能(Adaboosting算法)
3)隨機森林——基于樣本隨機性和屬性隨機性
一、機器學習概念
機器學習就是將傳感器等方式得到的海量的數據轉化為有用的信息的過程。就是根據以往的經驗和數據使得構建的模型最優,以此來更加滿足需求。
二、機器學習步驟
1、采集數據——拍照、傳感器等
2、輸入數據——如輸入圖像
3、分析數據——提取特征
4、訓練算法——對于無監督學習來說不需要訓練,否則需要訓練
5、測試算法——指標衡量算法的可靠性、泛化能力等
6、使用算法
三、有監督學習
1、k-近鄰算法
核心思想
核心思想:首先有一批樣本數據集合,我們稱之為訓練數據集,并且我們知道他們的標簽,即每個樣本和類別的對應關系是確定的。當一個不帶標簽的新樣本輸入時,我們先提取這個樣本的特征值,然后計算這個樣本和訓練集中每一個樣本對應特征值的距離,距離從小到大取k個點,然后分別統計這k個點的類別分別是什么,將這k個點中出現最多的標簽作為這個新樣本的標簽。
距離:歐式距離——每個特征值的差的平方和,再開根號
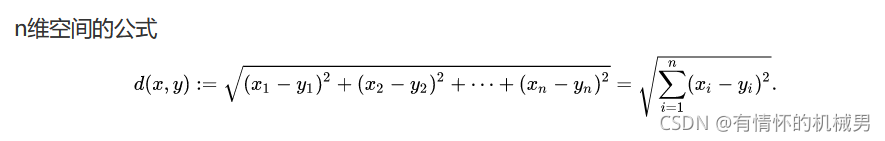
注:雖然是有監督算法,但是不需要進行訓練,因為是臨時利用所有的訓練樣本的特征值,這也造成了這個算法預測時間長。
實例:手寫數字的識別
https://blog.csdn.net/qq_41661809/article/details/89409724
1)先獲得公開數據集0--1手寫黑白圖像
2)將32*32的黑白圖像按行轉換成1*1024的向量,并且帶有標簽
3)將新輸入的黑白圖像的向量和每一個圖像的向量進行距離計算
4)從小到大排列距離,取前k個樣本;
5)統計k個樣本的不同類別個數;
6)將最多的類別數作為新樣本的標簽
優缺點:
優點:易于實現、理解
缺點:效率不高,每次預測都要進行大量的計算,時間長
2、決策樹
相關概念
熵:度量數據集的混亂程度,越大越亂

信息增益:與熵相反,越大數據越有序
核心思想
核心思想:
訓練階段:已知一個數據集,數據集包含屬性值和標簽,每一條數據樣本包含若干個屬性值和一個標簽,這作為訓練數據集。決策樹的決策就在于決定用哪一個屬性去劃分數據集,這個時候就使用到了熵或者信息增益,計算以每一個屬性進行劃分數據集后的各個子數據集的熵,然后將劃分后熵最小的那個屬性作為當前結點的劃分屬性依據,根據這個屬性數據集會被劃分成多個數據集,然后對每一個子數據集根據熵來確定劃分屬性,注意這里的屬性要去掉父節點的屬性。然后遞歸就得到了一顆樹。
訓練得到的是一顆結點是屬性值的樹,葉子節點為標簽值,我們稱之為決策樹,一般可以利用字典去存放這棵樹,父節點屬性值作為key,子樹作為value。
預測階段:新輸入一個樣本,我們根據樣本的屬性的值和決策樹來決定樣本的標簽
一些小技巧
剪枝:因為在構造決策樹的時候,我們是用的遞歸,會遍歷所有的情況,耗時較長,我們其實可以通過剪枝的方式來決定要不要繼續遞歸,若劃分后的正確率下降了,那我們則停止這個屬性的遞歸,換下一個屬性進行嘗試。
連續值處理:若碰到是數值型的話,那我們可以先對這些數值進行排序,然后將兩個數的均值作為一個劃分屬性。
優缺點
優點:計算復雜度不高、結果易于理解、對中間的缺失不敏感
缺點:可能產生過度匹配的問題
典型算法:ID3、C45
3、神經網絡
具體相關見專欄:【機器學習】神經網絡BP理論與python實例系列
神經網絡會出現局部最優的情況,為了解決這個問題有以下幾種方法:
1)模擬退火:在每一步都會以一定的概率去接受比最優解差的次優解,有助于跳出“局部最優”,但是隨著時間推移,這個概率應該減小
2)選取多組參數初始值,訓練后選取誤差最小的一組參數作為最終的參數。雖然都會陷入不同的局部極小,但是這樣可以盡可能地接近全局最優
3)隨機梯度下降法:計算梯度的時候增加隨機因素
4)遺傳算法
5)預訓練模型:在深度學習中,重新進行參數初始值的設置會非常麻煩,因為量大,而預訓練模型則是一層一層進行訓練,每一層的輸入是上一層的輸出,這一層的輸出又是下一層的輸入,這樣就得到了一個預訓練的模型,這時候我們在往后的模型中就可以拿這些參數值作為初始值。總結即先尋找每一組參數的局部最優,然后用于后續的全局尋優,因此一個好的初訓練模型,也能幫助避免“局部最優”。
4、SVM——支持向量機
核心思想
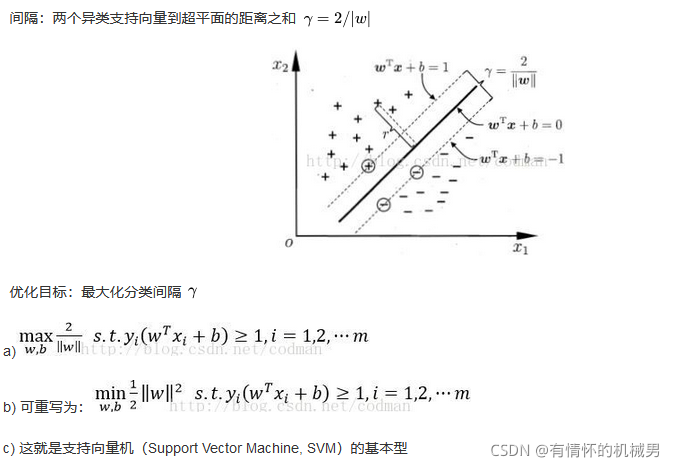
核心思想:這個的核心思想其實就是找到一個平面將不同的兩類分割開。這個平面的特點為:
w^T*x + b = 0
參數需要滿足最接近直線的幾個點有:w^T*x + b = (+-)1
這幾個點稱之為支持向量
1)怎么尋找支持向量?
使得經過支持向量的兩條線間隔最大:dist = 2/||w||
超平面函數*標簽始終大于等于1
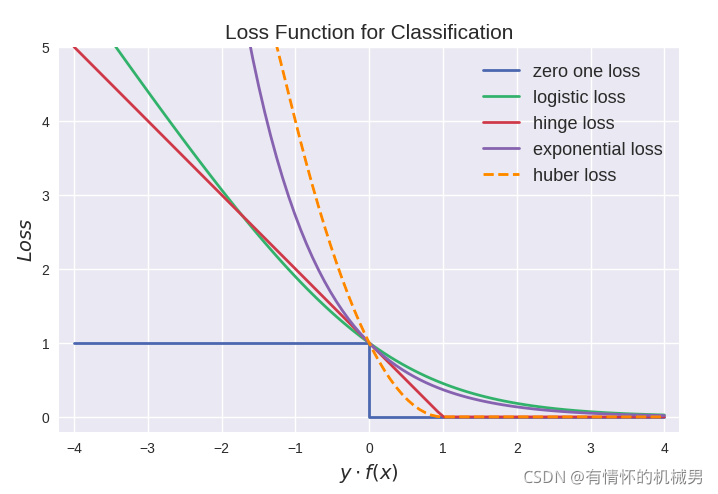
因此進行損失函數的選擇的時候,一般取標簽和超平面函數的乘積作為變量,常用的分類損失函數有0-1損失函數、hinge損失函數、對數損失函數,常用的是hinge函數,h = max(0,1-yf(x))
具體損失函數可以參見:【深度學習】——分類損失函數、回歸損失函數、交叉熵損失函數、均方差損失函數、損失函數曲線
因為分類問題只有-1,1兩種類型,因此使用真實標簽乘以超平面函數(預測標簽)的乘積作為損失函數的變量。預測真確則大于1,否則小于1,而不是去計算誤差多少。
SVM和SVR的區別
參考:談談SVM和SVR的區別
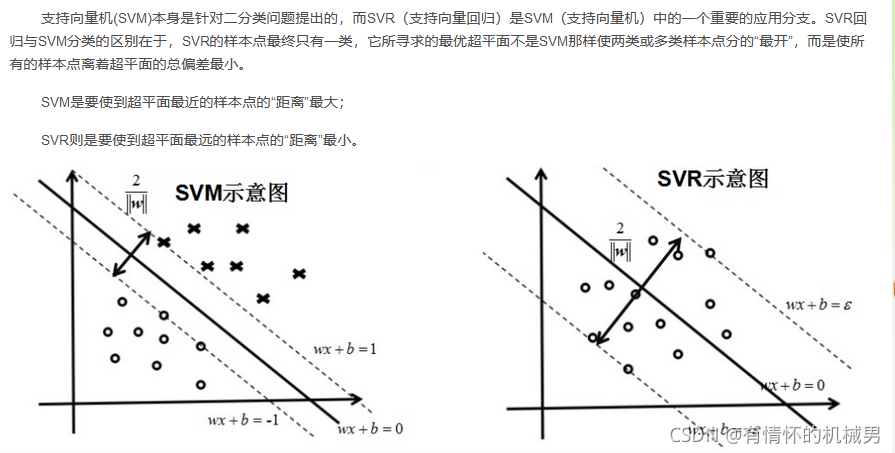
 優缺點
優缺點
優點:泛化錯誤率低、計算開銷不大
缺點:對參數調節和核函數調節很敏感,若SVM不修改的話僅適合二分類問題
?5、集成學習或元算法
核心思想
核心思想:集成學習(ensemble method)和元算法(meta-algorithm)就是將不同的分類器進行組合成一個新的分類器。
組合形式:
1)針對同一個數據集訓練多個不同分類器(SVM、K-NN等),然后結合起來
2)針對不同的數據集訓練不同數據集,訓練同一種分類器,然后結合起來
3)不同數據集不同分類器
即先訓練多個弱分類器,然后再結合在一起得到一個強分類器
常見的元算法或者集成學習——串行bagging(隨機森林等)、并行boosting(自適應boosting--adaboosting等)
參考:機器學習算法 之 集成學習:串行-Boosting族(AdaBoost),并行-Bagging、隨機森林
0)串行訓練與并行訓練
并行訓練:每個數據集獨立分開訓練,互不影響
串行訓練:下一個訓練器的訓練受上一個訓練結果的影響
1)bagging(自舉匯聚法)——基于數據隨機重抽樣的分類器構建
核心思想:不同數據集(重抽樣重組而得)、同一種分類器,即在原始數據集中重抽樣得到多個數據集,每個數據集訓練得到一個分類器,最后根據分類器結果的投票結果進行決策
①假設原始數據集大小為n,從原始數據集中有放回的抽取一個樣本;
②抽取n個樣本組成了一個新的和原始數據集一樣大的數據集,因為是有放回抽樣,因此元素可以是重復的
③重復步驟①②S次,這樣就得到了S個和原始數據大小一樣的新數據集
④對這S個數據集進行獨立訓練得到S個分類器;——并行訓練
⑤預測階段:輸入新樣本,得到S個預測結果,然后根據投票的方式,將票數最高的分類結果作為最終分類標簽——這里也看出對于每一個分類器的結果的權重都是一樣的,都為1
常見的bagging算法有:隨機森林(RF)
2)boosting——基于錯誤提升分類器的性能(Adaboosting算法)
核心思想:同一數據集(每個樣本帶權重)、同一種分類器,即集中關注上一個分類器訓練錯誤的樣本進行下一個分類器的訓練
這里以Adaboosting算法為例:
①對訓練樣本集的每一個樣本賦予相等的權重
②先訓練一個分類器,記錄訓練后預測錯誤的樣本;
③根據分類器的錯誤率,對每一個分類器也有一個權重alpha,基于錯誤率計算得到的

④調整樣本權重:分類正確的樣本權重降低,錯誤的增加;權重主要是用于后續預測和損失函數使用,讓分類器更關注這些樣本

⑤再對調整后的數據集進行訓練,得到下一個分類器;——串行訓練
⑥重復③-⑤,直到分類器的錯誤率為0或者分類器達到指定個數時停止迭代
⑦迭代后的如下圖所示,預測階段是將樣本輸入后,得到的預測結果會進行alpha加權后再相加得到最終結果
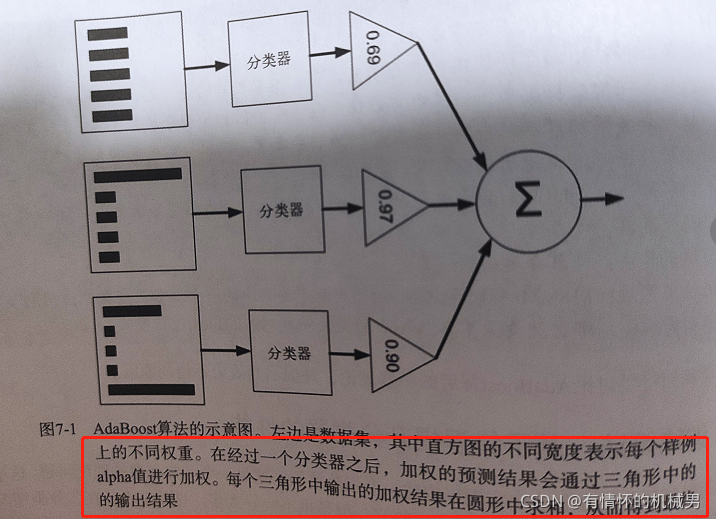
3)隨機森林——基于樣本隨機性和屬性隨機性
核心思路:其實就是基于決策樹進行的隨機改進,這里是隨機選擇一個含有k個屬性的自己,然后從這個子集中找到一個最優劃分屬性用于劃分。這樣就會得到多個決策樹,進行投票即可
?四、無監督學習
1、聚類
參考:https://zhuanlan.zhihu.com/p/104355127
核心思想
聚類就是物以類聚,首先得到的是一個沒有標記的樣本集,我們希望將其劃分成不同的類簇,即不同的子集。首先我們隨機選擇K個樣本作為每個類簇的中心,然后計算每個樣本和所有中心的距離,將距離最近的類簇中心作為這個樣本的類簇,然后更新類簇中心,直到不改變為止
基本步驟——這里以K均值聚類為例(K-Mean)
1)隨機選取K個樣本作為初始均值向量(簇中心);
2)計算樣本i和k個簇質心的距離得到距離向量distij;
3)將樣本i歸類到min(distij)的簇j中;
4)待所有樣本劃分結束后,更新均值向量
5)求劃分后每一個簇的樣本的均值(幾何中心),作為新的均值向量
6)重復2)-5)
7)直到均值向量不再改變,或者經過多少次迭代后停止即可
8)給每一個類簇定義上類標簽,這樣就聚類完成了
分類
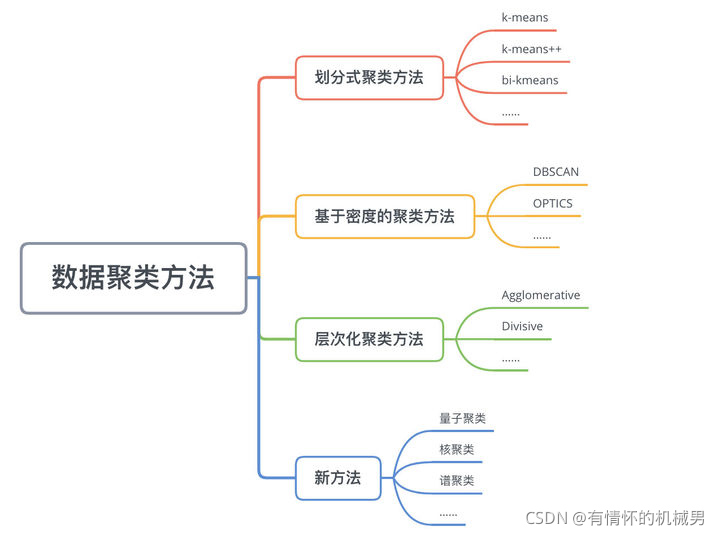
?
?
K-均值聚類、密度聚類(DBSCAN算法)、層次聚類、高斯混合聚類等
目標
簇內距離最小,簇間距離最大
?





)





)





)

)
