一、什么是過擬合？（overfitting）

二、過擬合的表現（判定方法）

?訓練集、測試集、驗證集區別

?測試集與驗證集的區別

?三、產生過擬合的原因

1、樣本方面

2、模型方面

四、避免過擬合的方法

1、樣本方面

1）增加樣本量

2）樣本篩選（特征降維、特征選擇）

3）歸一化數據樣本

2、模型方法

1）正則化——使模型簡單化、參數稀疏化

????????①概念——核心思想

問題1：什么是稀疏參數？什么是數據的稀疏性？

問題2：什么是范數？常用的范數函數是什么？

問題3：實現參數的稀疏有什么好處嗎？

問題4：參數值越小代表模型越簡單嗎？

????????②L0正則化——正則項為非零分量的個數

????????③L1正則化（LASSO）——效果使w分量往0靠攏

????????④L2正則化（嶺回歸）——效果使參數減小

????????⑤為什么可以避免過擬合？

????????⑥比較L1與L2

2）歸一化（Normalization）

????????①最小最大值歸一化（min-max normalization）

?????????②0均值標準化（Z-score standardization）

????????③batch normalization(BN層)

??????? ④什么情況下使用歸一化方法？

????????⑤為什么歸一化能夠實現避免過擬合？

???????? ⑥BN的優點

3）dropout（隨機丟棄）——隨機刪除一些神經元，以在不同批量上訓練不同的神經網絡架構。

?????????①過程

??????? ②為什么能夠避免過擬合?

4）early stopping（早停法）

?①第一類停止標準

?????????②第二類停止標準

?????????③第三類停止標準

?????????④選擇停止標準的規則

????????⑤ 優缺點

一、什么是過擬合？（overfitting）

過擬合其實就是為了得到一致假設而使得假設過于地嚴格。使得其在訓練集上的表現非常地完美，但是在訓練集以外的數據集卻表現不好。

?如上圖所示，紅線就是過擬合了，雖然它在訓練集上將所有的點都放在了線上，但是如果再來一個點就會不起作用，這就是過擬合，而綠線的話也比較好地擬合了點集，但是它的泛化能力相較于紅線來說是更好的

二、過擬合的表現（判定方法）

1、訓練集的正確率不增反減

2、驗證集的正確率不再發生變化

3、訓練集的error一直下降，但是驗證集的error不減反增

上圖所示，訓練集隨著訓練的過程中，error一直減小，但是訓練次數到了一定程度的時候，驗證集的error卻開始上升，這時候說明當前代數訓練得到的模型對于訓練集的樣本表現良好，但是對于訓練集以外的樣本表現不太好。

?訓練集、測試集、驗證集區別

參考：https://blog.csdn.net/kieven2008/article/details/81582591

訓練集：計算梯度更新權重，用于訓練得到模型

驗證集：用于每次訓練完一代后判斷模型的訓練情況，根據在驗證集上的正確率來進行產參數的調整，一定程度上可以避免過擬合

測試集：用于判斷最終訓練出來的模型表現情況，比如給出一個accuracy以推斷網絡的好壞等

?測試集與驗證集的區別

?三、產生過擬合的原因

參考：什么是「過擬合」，如何判斷，常見的原因是什么？

1、樣本方面

1）用于訓練的樣本量過于少，使得訓練出來的模型不夠全面以致于使用模型時錯誤率高

比如對于貓這類動物，如果訓練數據集中只有一個正拍且坐立的貓，那么當過擬合時，模型往往有可能只能識別出這類姿態的貓，像跳躍的貓、局部捕捉的貓、反轉的貓等等可能都識別不出來了

2）訓練的樣本量噪聲大（質量不好），導致一些錯誤的特征錯認為是學習的對象，使得訓練模型不夠健壯

2、模型方面

1）參數過多，模型過于復雜

2）選擇的模型本身就不適用于當前的學習任務

3）網絡層數過多，導致后面學習得到的特征不夠具有代表性

四、避免過擬合的方法

參考：

https://blog.csdn.net/baidu_31657889/article/details/88941671

https://www.cnblogs.com/ying-chease/p/9489596.html

https://zhuanlan.zhihu.com/p/97326991

解決問題往往是從出現問題的原因入手，所以根據上面的過擬合原因來來避免過擬合

1、樣本方面

1）增加樣本量

深度學習中樣本量一般需要在萬級別才能訓練出較好的模型，且樣本盡可能地多樣化，使得樣本更加地全面。一般通過圖像變換可以進行數據增強，見文章《【tensorFlow】——圖像數據增強、讀取圖像、保存圖像》

2）樣本篩選（特征降維、特征選擇）

參考：機器學習-->特征降維方法總結

特征降維：PCA等，根據現有的特征創造出新的特征

特征選擇：選擇具有代表性的特征參與訓練

3）歸一化數據樣本

改變數據的分布，使得更集中在激活函數的敏感區，具體見下面2（2）知識點

2、模型方法

1）正則化——使模型簡單化、參數稀疏化

參考：

https://blog.csdn.net/qq_20412595/article/details/81636105

????????①概念——核心思想

正則化其實就是在原來的損失函數后面增加了一項加數，這項加數稱之為正則項，這個正則項通常由一個系數和范數的乘積的累加和構成。其主要是通過正則項來限制權重w參數的值的變化，使其盡可能的小或者盡可能地趨于0，以達到稀疏參數的效果，進而使得模型復雜度下降，避免過擬合。

問題有以下幾個？

問題1：什么是稀疏參數？什么是數據的稀疏性？

稀疏參數：使得模型中參數的零分量盡可能地多；

數據的稀疏性：在特征選擇中的概念，指的是在眾多的特征中，有的特征對于模型的優化是無關的，這就是數據存在稀疏性，可以通過特征選擇來選擇有價值的特征。

但是在機器學習的參數中，由于參數眾多，模型復雜度過于高的話，易出現過擬合現象，因此我們需要通過增加參數的稀疏性來降低復雜度，進而避免過擬合。

問題2：什么是范數？常用的范數函數是什么？

范數：在泛函分析中，它定義在賦范線性空間中，并滿足一定的條件，即①非負性；②齊次性；③三角不等式。它常常被用來度量某個向量空間（或矩陣）中的每個向量的長度或大小

問題3：實現參數的稀疏有什么好處嗎？

一個好處是可以簡化模型，避免過擬合。因為一個模型中真正重要的參數可能并不多，如果考慮所有的參數起作用，那么可以對訓練數據可以預測的很好，但是對測試數據表現性能極差。另一個好處是參數變少可以使整個模型獲得更好的可解釋性。

問題4：參數值越小代表模型越簡單嗎？

是的。為什么參數越小，說明模型越簡單呢，這是因為越復雜的模型，越是會嘗試對所有的樣本進行擬合，甚至包括一些異常樣本點，這就容易造成在較小的區間里預測值產生較大的波動，這種較大的波動也反映了在這個區間里的導數很大，而只有較大的參數值才能產生較大的導數。因此復雜的模型，其參數值會比較大。反過來就是如果參數值小的話，那么異常點在這個區間里的導數就會比較小，造成預測值的波動也就小，這樣就會利于模型，避免過擬合，更具有泛化能力去預測新樣本。

????????②L0正則化——正則項為非零分量的個數

利用非零參數的個數，可以很好的來選擇特征，實現特征稀疏的效果，具體操作時選擇參數非零的特征即可。但因為 $L_{0}$ 正則化很難求解，是個NP難問題，因此一般采用 $L_{1}$ 正則化。 $L_{1}$ 正則化是 $L_{0}$ 正則化的最優凸近似，比 $L_{0}$ 容易求解，并且也可以實現稀疏的效果

????????③L1正則化（LASSO）——效果使w分量往0靠攏

?在原始的代價函數后面加上一個L1正則化項，即所有權重w的絕對值的和，乘以λ/n（這里不像L2正則化項那樣，需要再乘以1/2）

加上L1正則項后的損失函數：

?對權重參數求導：

更新權重參數：

sgn(w)函數是w小于0時函數值為-1，等于0時為0，大于0時函數值為1

其中λ和n參數大于0，由權重參數的更新可以看出，當w為正時，更新后的w變小。當w為負時，更新后的w變大——因此它的效果就是讓w往0靠，使網絡中的權重盡可能為0，也就相當于減小了網絡復雜度，防止過擬合。

????????④L2正則化（嶺回歸）——效果使參數減小

L2正則化就是在代價函數后面再加上一個正則化項，即所有權重w的平方和，乘以λ/n需要再乘以1/2，方便后續的求導。

?加上L2正則項后的損失函數：

?對權重參數求導：

更新權重參數：

在不使用 $L_{2}$ 正則化時，求導結果中w前系數為1，現在w前面系數為? $(1-\frac{\eta \lambda }{n})$ ?，因為η、λ、n都是正的，所以?1-η*λ/n小于1，它的效果是減小w，這也就是權重衰減（weight decay）的由來。當然考慮到后面的導數項，w最終的值可能增大也可能減小。根據奧卡姆剃刀法則可知，更小的權值w，從某種意義上說，表示網絡的復雜度更低，對數據的擬合剛剛好。

????????⑤為什么可以避免過擬合？

其實就是增加正則項后，使得參數變小了，模型簡化，使得損失在避免過擬合和最小化損失之間進行了折中，以此來避免了過擬合。

????????⑥比較L1與L2

假設正則項為（p-范數）：

假設w向量分量由兩個分量組成的，即w = w1 + w2，其中w,w1,w2均為向量，則當p取不同的值的時候就可以得到他們的曲線圖，假設Lp=C，其中C為常數值，則當p取0.5,1,2,4的圖如下

????? ??????

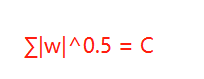
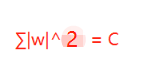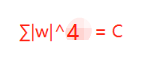
?這時候我們假設原先的損失函數為：

則令其等于C，則可以繪制出曲線（平方誤差項等值線）：

上圖是L1，L2，平方誤差項取一系列的常數值C得到的（C1,C2,C3等）

當1-范數（L1）、2-范數（L2）、平方誤差項都取相等的值時，我們損失函數為了取得最小的損失，因為正則化后的損失不再單單為了損失最小，而是還得考慮避免過擬合，因此需要在二者之間平衡，對應于圖像中就是Lp與平方誤差項曲線相交點。

藍色的圓圈表示沒有經過限制的損失函數在尋找最小值過程中，w的不斷迭代（隨最小二乘法，最終目的還是使損失函數最小）變化情況，表示的方法是等高線，z軸的值就是?E(w)
w??最小值取到的點

可以直觀的理解為（幫助理解正則化），我們的目標函數（誤差函數）就是求藍圈+紅圈的和的最小值（回想等高線的概念并參照式），而這個值通在很多情況下是兩個曲面相交的地方

L1和平方誤差項曲線相交于坐標點，即w1或w2等于0，但是L2和平方誤差項曲線相較于非零點，這就說明了L1會比L2更易于得到稀疏解。但是L1曲線具有拐點，即并不是處處可導，給計算帶來了很大的不便（這也是改進的方向所在）。而L2處處平滑，便于求導。

2）歸一化（Normalization）

歸一化就是改變數據分布，將大范圍的數據限定在一個小范圍，或者使其呈一定規律的分布

常用的歸一化方法有：min-max normalization、Z-score standardization

????????①最小最大值歸一化（min-max normalization）

將樣本的范圍限制在一定確定的小范圍中，一般取【0,1】或者【-1,1】

歸一化到【0,1】之間：

歸一化到【-1,1】之間：

其中：max表示數據集中的最大值，min表示數據集中的最小值，mean表示數據集的均值

?????????②0均值標準化（Z-score standardization）

參考：https://www.jianshu.com/p/26d198115908

規范了數據的分布，將數據分布改變成了標準的正態分布，即均值為0，標準差為1的分布

均值

?標準差

?歸一化后的數值

????????③batch normalization(BN層)

參考：

https://www.cnblogs.com/guoyaohua/p/8724433.html

https://zhuanlan.zhihu.com/p/93643523

BN層常用于深度學習中，因為深度學習中的樣本量大，一般都是分批進行訓練的，即batch，因此進行歸一化時是對一個batch進行歸一化，而不是對整個訓練集進行歸一化

?這里的BN其實本質就是zero-score standardization，只是這里添加了兩個可以訓練的參數r和β。在深度學習中，往往輸入的是圖像，每個batch是一部分圖像，通過對這部分輸入進行歸一化后輸入到下一層網絡中，例子如下：

其中兩個參數的意義？

稍微了解神經網絡的讀者一般會提出一個疑問：如果都通過BN，那么不就跟把非線性函數替換成線性函數效果相同了？這意味著什么？我們知道，如果是多層的線性函數變換其實這個深層是沒有意義的，因為多層線性網絡跟一層線性網絡是等價的。這意味著網絡的表達能力下降了，這也意味著深度的意義就沒有了。所以BN為了保證非線性的獲得，對變換后的滿足均值為0方差為1的x又進行了scale加上shift操作(y=scale*x+shift)，每個神經元增加了兩個參數scale和shift參數，這兩個參數是通過訓練學習到的，意思是通過scale和shift把這個值從標準正態分布左移或者右移一點并長胖一點或者變瘦一點，每個實例挪動的程度不一樣，這樣等價于非線性函數的值從正中心周圍的線性區往非線性區動了動。核心思想應該是想找到一個線性和非線性的較好平衡點，既能享受非線性的較強表達能力的好處，又避免太靠非線性區兩頭使得網絡收斂速度太慢。

??????? ④什么情況下使用歸一化方法？

??????? 這里主要講BN層。在深度學習當中，每一層網絡的輸入都可以作為下一層網絡的輸入，開始的時候我們會將樣本進行歸一化后傳輸給網絡，但是到了隱層，由于中間激活函數等非線性函數的映射，使得原本的歸一化輸入的數據分布發生了改變，這樣使得下一層的輸入的數據分布和上一層的數據分布是不一樣的，即每一層輸入的數據的分布都是變化的，這個問題稱之為Internal Covariate Shift，這樣就導致了訓練的收斂速度變慢了。因此我們一般會在激活層之前，卷積層之后使用BN層，這樣就能夠保證每次輸入到網絡中的數據分布都是標準的正態分布，這也加快了訓練的收斂速度。

????????⑤為什么歸一化能夠實現避免過擬合？

參考：https://www.cnblogs.com/guoyaohua/p/8724433.html

BN的基本思想其實相當直觀：因為深層神經網絡在做非線性變換前的激活輸入值（就是那個x=WU+B，U是輸入）隨著網絡深度加深或者在訓練過程中，其分布逐漸發生偏移或者變動，之所t以訓練收斂慢，一般是整體分布逐漸往非線性函數（激活函數）的取值區間的上下限兩端靠近（即梯度會逐漸趨于0，導致梯度消失，參數更新慢）（對于Sigmoid函數來說，意味著激活輸入值WU+B是大的負值或正值），所以這導致反向傳播時低層神經網絡的梯度消失，這是訓練深層神經網絡收斂越來越慢的本質原因，而BN就是通過一定的規范化手段，把每層神經網絡任意神經元這個輸入值的分布強行拉回到均值為0方差為1的標準正態分布，其實就是把越來越偏的分布強制拉回比較標準的分布，這樣使得激活輸入值落在非線性函數對輸入比較敏感的區域（也就是將最大的值），這樣輸入的小變化就會導致損失函數較大的變化，意思是這樣讓梯度變大，避免梯度消失問題產生，而且梯度變大意味著學習收斂速度快，能大大加快訓練速度。

　　THAT’S IT。其實一句話就是：對于每個隱層神經元，把逐漸向非線性函數映射后向取值區間極限飽和區靠攏的輸入分布強制拉回到均值為0方差為1的比較標準的正態分布，使得非線性變換函數的輸入值落入對輸入比較敏感的區域，以此避免梯度消失問題。因為梯度一直都能保持比較大的狀態，所以很明顯對神經網絡的參數調整效率比較高，就是變動大，就是說向損失函數最優值邁動的步子大，也就是說收斂地快。BN說到底就是這么個機制，方法很簡單，道理很深刻。

可以看以下兩個圖：

沒有歸一化前 ???????

一開始沒有歸一化的時候數據分布是上左圖藍色曲線（第二高），這時候假設后面的激活函數是sigmoid函數（上右圖第三高），可以發現大部分的數據都是分布在了sigmoid的左邊部分，sigmoid的左邊可以看到值逐漸趨于飽和區（即梯度趨于0），對應到下圖的梯度來看，可以看到梯度值接近于0了，這時候就會使得參數的更新速度非常慢，使得模型訓練的收斂速度很慢。

歸一化后

??????? 而我們使用BN層后，數據分布呈均值為0方差為1的標準正態分布，這時候的數據分布如上左圖的紫色所示。可見大部分數據都是集中在了sigmoid的梯度較大的部分，且關于0對稱，這樣一來，保證了梯度處于較大區域，梯度也就更新的快了。

怎么保證非線性（兩個參數的作用）

??????? 我們不妨會有個疑問，既然每次輸入到非線性層的時候要使得數據分布一致，那直接使用線性函數不就好了，但是我們需要知道的是，多層線性和一層線性的效果是一樣的，這樣會導致模型的表達能力不強，因此BN層為了能夠得到非線性能夠，又在原有的z-score歸一化方法上加了兩個參數r和β，就是為了能夠找到一個線性和非線性的1平衡點，對應到上左圖的曲線表征是，曲線變窄或變寬對應最高和最矮的曲線，這使得數據分布稍微地發生了移動，使得數據保留了一定的非線性。

?
?

???????? ⑥BN的優點

?????? 不僅僅極大提升了訓練速度，收斂過程大大加快；

??????? 增加分類效果，一種解釋是這是類似于Dropout的一種防止過擬合的正則化表達方式，所以不用Dropout也能達到相當的效果；

????????另外調參過程也簡單多了，對于初始化要求沒那么高，而且可以使用大的學習率等。

筆記

3）dropout（隨機丟棄）——隨機刪除一些神經元，以在不同批量上訓練不同的神經網絡架構。

參考：

https://zhuanlan.zhihu.com/p/266658445

概念：我們在前向傳播的時候，讓某個神經元的激活值以一定的概率p停止工作，這樣可以使模型泛化性更強，因為它不會太依賴某些局部的特征。每次迭代丟失的神經元都不一樣，使得其訓練得到了不一樣的模型。

?????????①過程

?輸入是x輸出是y，正常的流程是：我們首先把x通過網絡前向傳播，然后把誤差反向傳播以決定如何更新參數讓網絡進行學習。使用Dropout之后，過程變成如下：

（1）首先隨機（臨時）刪掉網絡中一半的隱藏神經元，輸入輸出神經元保持不變（圖中虛線為部分臨時被刪除的神經元）

（2）然后把輸入x通過修改后的網絡前向傳播，然后把得到的損失結果通過修改的網絡反向傳播。一小批訓練樣本執行完這個過程后，在沒有被刪除的神經元上按照隨機梯度下降法更新對應的參數（w，b）。

（3）然后繼續重復這一過程：

a. 恢復被刪掉的神經元（此時被刪除的神經元保持原樣，而沒有被刪除的神經元已經有所更新）

b. 從隱藏層神經元中隨機選擇一個一半大小的子集臨時刪除掉（備份被刪除神經元的參數）。

c. 對一小批訓練樣本，先前向傳播然后反向傳播損失并根據隨機梯度下降法更新參數（w，b）（沒有被刪除的那一部分參數得到更新，刪除的神經元參數保持被刪除前的結果）。

不斷重復這一過程。

??????? ②為什么能夠避免過擬合?

1、多平均模型：不同的固定神經網絡會有不同的過擬合，隨機丟棄訓練得到不同的神經網絡，多個神經網絡取平均可能會抵消掉過擬合，多模型類似于多數投票取勝的策略；

2、減少神經元之間的依賴：由于兩個神經元不一定同時有效，因此減少了兩個神經元之間的依賴性，使得神經元更加地獨立，迫使神經網絡更加地魯棒性；因為神經網絡不應該對特點的特征敏感，而是對眾多特征中學習規律；

3、生物進化：這個其實優點像遺傳算法中采用的生物進化，為了適應新環境而會在雌雄間各取一半基因