目錄

梯度

梯度下降

常用的梯度下降算法（BGD，SGD，MBGD）

梯度下降的詳細算法

算法過程

批量梯度下降法（Batch Gradient Descent）

隨機梯度下降法（Stochastic Gradient Descent）

小批量梯度下降法（Mini-batch Gradient Descent）

?梯度下降的優化算法

存在的問題

梯度下降優化的方法

?機器學習中具體梯度下降的優化算法

基于陷入局部最優的問題的優化

Momentum算法

基于學習率方面進行的梯度優化

Adam算法（Adaptive Moment Estimation）

---

參考：梯度下降（Gradient Descent）小結

梯度

概念：在微積分里面，對多元函數的參數求?偏導數，把求得的各個參數的偏導數以向量的形式寫出來，就是梯度。

?意義：梯度是函數在當前位置變化最快的方向，因此可以使得損失函數很快地找到極值，損失一般是找極小值，進而用于指導訓練模型中參數的更新。?

梯度下降

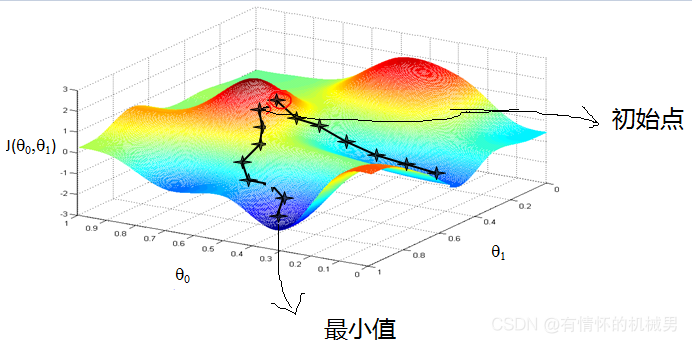
????????首先來看看梯度下降的一個直觀的解釋。比如我們在一座大山上的某處位置，由于我們不知道怎么下山，于是決定走一步算一步，也就是在每走到一個位置的時候，求解當前位置的梯度，沿著梯度的負方向，也就是當前最陡峭的位置向下走一步，然后繼續求解當前位置梯度，向這一步所在位置沿著最陡峭最易下山的位置走一步。這樣一步步的走下去，一直走到覺得我們已經到了山腳。當然這樣走下去，有可能我們不能走到山腳，而是到了某一個局部的山峰低處。

具體實施：從整體來看，當點下降最快的方向不是由某一個維度的偏導決定的1，而是由所有維度的偏導共同決定的，這也符合“梯度是變化最快的方向”和“梯度是函數對所有參數求偏導后的值的向量”這兩個說法。在實際實施中，我們一般是通過偏導來指導不同參數的更新，以此來做到函數值下降得最快（梯度方向）。這就是梯度下降的本質。

????????從上面的解釋可以看出，梯度下降不一定能夠找到全局的最優解，有可能是一個局部最優解。當然，如果損失函數是凸函數，梯度下降法得到的解就一定是全局最優解。

常用的梯度下降算法（BGD，SGD，MBGD）

梯度下降的詳細算法

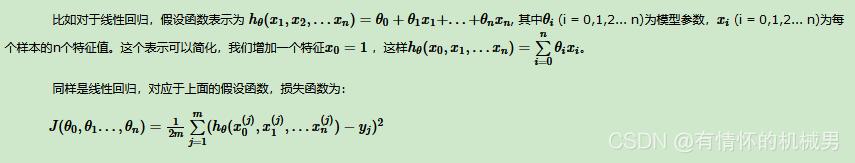
算法過程

一般有兩種方法，一種迭代，一種矩陣運算，具體見：梯度下降（Gradient Descent）小結

批量梯度下降法（Batch Gradient Descent）

?優點：對于準確率來說，因為使用了全部樣本的梯度，所以準確率會更高

缺點：但是使用了全部樣本，導致在訓練速度和收斂速度上都比較慢

隨機梯度下降法（Stochastic Gradient Descent）

?優點：隨機梯度下降就是BGD的極端，只是隨機選擇一個樣本的梯度來指導梯度的下降，因為使用了一個樣本，因此其訓練速度會很快

缺點：但是非常依賴于初始值和步長的影響，有可能會陷入局部最優中，導致收斂速度慢

小批量梯度下降法（Mini-batch Gradient Descent）

在深度學習中，SGD和MBGD統稱為SGD

這個梯度下降算法其實就是結合了BGD和SGD兩者，采用了小批次的梯度來進行計算。

優點：分擔了訓練壓力（小批量）、加快收斂

缺點：初始學習率難以確定、容易陷入局部最優

?梯度下降的優化算法

存在的問題

BGD、SGD以及MBGD都是比較常見的梯度算法，但是都存在以下問題：

1）學習步長（學習率）難以確定，是超參數，太大導致跳過最優解，太小收斂速度慢，可能會導致陷入局部最優；

2）參數初始值的確定，不同初始值有可能會產生不同的最優解，比如初始值分別在兩座山的山頂，那得到的山腳位置自然是可能不一樣的；

3）樣本特征值的差異性大，變化范圍大

梯度下降優化的方法

?機器學習中具體梯度下降的優化算法

基于陷入局部最優的問題的優化

Momentum算法

Momentum算法是在MBGD的基礎上進行了修改，即在梯度方向上增加動量（Momentum），意思指在更新梯度時，會保留之前更新的梯度方向，然后利用當前批次的梯度進行微調

優點：

1）能夠抑制梯度的震蕩，在梯度與上次相同的時候梯度下降多一點，反之少一點

2）有可能跳出局部極值

基于學習率方面進行的梯度優化

Adam算法（Adaptive Moment Estimation）

優點：

1）每一次迭代的學習率都在依次確定的范圍內 ，使得參數更新更加地穩定

2）使模型更加地收斂，適用于深層網絡和較為復雜的場景

參考文獻

https://blog.csdn.net/liuy9803/article/details/81780543

https://www.cnblogs.com/pinard/p/5970503.html

物體檢測書籍