引言

眨眼間已經12月了，眼看著2023年馬上要過完了。

女朋友最近總說，工作以后感覺時間過的好快。事實上，我也是這么認為的。年紀越大，越會擔心35歲危機的降臨。所以，人還是應該持續學習和進步的。具體來說，就是在工作時間之外，每年都能有一些關于自身的成長。

23年初，我給自身成長設置了一系列目標，其中之一就是體系化。這里的體系化，主要包含兩項，第一項是運籌學基礎算法的體系化，第二項是機器學習算法的體系化。到了年尾，應該為一年的工作做一個總結了。

本文將著重分享今年在第一項（運籌學基礎算法）上的實踐和總結，后續文章將再聊另外一個內容。

正文見下。

目標設計

科學體系化的方式，私以為應該是參考各種專業書的目錄，然后結合自己的認知，做個性化設計。 舉個例子，《運籌學》（清華大學出版社）這本書是直接從線性規劃問題開始的，但是求解線性規劃問題的單純形法，對我來說已經比較復雜，不能算入門了。

下圖是我今年初給自己安排的體系化學習目標。

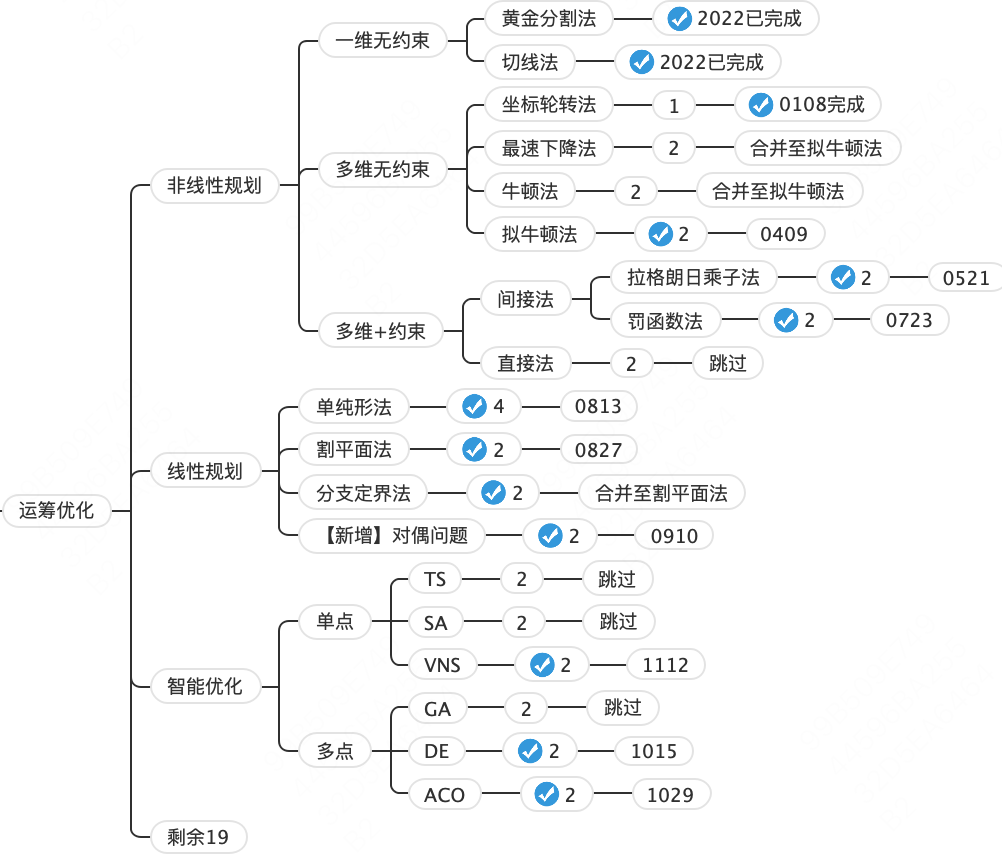
我認為，學習過程要從簡單到復雜。而最簡單的運籌問題，應該是一維無約束問題，在此基礎上再提升問題維度和增加不同類型的約束條件。這些內容，在我年初的體系化學習目標中被歸類為非線性規劃模塊。現在想來，“非線性規劃”這個模塊的標題并不是很準確，不過也沒想到更好的，就繼續用這個吧。

理解了以上普適性較好的基本算法體系后，我覺得才適合來研究線性/整數規劃這一類在實際業務中被廣泛研究的問題和對應的求解算法。

除了非線性規劃、線性規劃和整數規劃外，還要學習智能優化算法的主要原因，是我覺得這些算法的改進嘗試中，針對迭代方向和迭代步長的設計很有藝術感，雖然缺乏嚴格的數學證明，但在實踐中已經被證明為非常有效的手段。

目標實踐

對于大部分算法，我給自己預設的目標是兩周學習完，這樣最終評估下來能有19周的剩余時間。

從剩余時間來說，我給自己安排的計劃，算是比較寬松的。我一直覺得，工作和學習應該是為生活服務的，如果發生了沖突，那幸福的生活體驗應該放在第一位。所以我從一開始就沒想著給自己太大的壓力，如果覺得有些累了，偷懶玩游戲、看視頻，甚至只是無聊發呆，也不會有太大的負罪感。

實際也是如此——從完成度來看，我最后一篇文章是VNS，11月12號完成的，距離12月31號只剩6周，也就是說我在年中的時候荒廢了13周左右的時間。

我對算法學習完成的定義是，寫一篇與算法內容對應的文章，里面至少應該包含2個模塊：

第一個是用自己的邏輯描述清楚算法原理。我對自己的要求是，讓算法小白都能看懂內容，如果未來真的有機會教書育人，這應該是我寶貴的財富了；

第二個是自己編寫代碼實現算法全過程。我對自己的要求是，分別用Python和Java編程實現，以驗證自己是否真的理解了算法原理，同時提升代碼能力。

從實際完成度來看，每一個算法相關的文章都算是及格了。對算法原理的描述，我還是比較滿意的，特別是收到小伙伴們的暖心評論和留言時，都會備受鼓舞。在代碼實現方面，并沒有達到預期，開始階段一些簡單的算法還能用Python和Java分別實現，到了中后期算法復雜度提升后就有些力不從心了。在認清現實后，我去掉了使用Java實現算法過程的目標。針對特別復雜的算法，甚至都不要求自己手寫了。

看，我就是這么容易和自己和解。

文章匯總

本節匯總了近一年運籌學基礎算法的相關文章和鏈接，并按照此前的目標設計進行了分類。

分類	文章和鏈接
非線性規劃-黃金分割法	Python和Java代碼實現：黃金分割法求解一維最優化問題
非線性規劃-切線法	Python和Java代碼實現：切線法求解一維最優化問題
非線性規劃-坐標輪轉法	Python代碼實現：坐標輪換法求解多維最優化問題
非線性規劃-梯度類算法	梯度類算法原理：最速下降法、牛頓法和擬牛頓法 擬牛頓法：python代碼實現
非線性規劃-間接法	求解包含約束的最優化問題：拉格朗日乘子法和KKT條件
非線規劃-直接法	求解包含約束的最優化問題：罰函數法
線性規劃-單純形法	線性規劃和單純形法-原理篇 線性規劃模型-工程應用篇
線性規劃-整數規劃	求解整數規劃問題的割平面法和分支定界法 稍微憋個招，聊聊為什么不能止步于會調求解器
線性規劃-對偶問題	線性規劃對偶問題：理論推導和實際應用
智能優化-DE	差分進化算法，依舊強勢
智能優化-ACO	蟻群算法求包含34個國內城市的TSP，和最優解相差沒那么大
智能優化-ALNS	著實不錯的自適應大鄰域搜索算法ALNS

經驗總結

關于這一年來對于運籌算法的學習和感悟，總結如下：

首先，這些算法在運籌學中算是基礎內容。通過對這些知識點的學習和總結，我自身受益匪淺，在一定程度上彌補了我因為非科班出身導致基礎知識儲備的欠缺。不過這只是一個開始，隨著認知的提升，可能會發現未知的內容也越來越多，后續還有很多內容需要去慢慢探索。

其次，在學習上我是偏應用導向的。當初選擇運籌學作為自己未來長期從事的行業，主要是覺得把這些算法策略應用到實際場景中能帶來極大的成就感，所以我不太會執著于理論上的推導，在學習知識時，會優先選擇工業實踐中最常用的運籌算法，并輔以部分基礎的算法原理，以知其然并知其所以然。

最后，這些知識點的串聯方式是基于我目前的認知。圖中的分類僅依賴于我當前體系化學習的實踐路徑，算不上權威，可以作為大家構建自己知識體系的參考。

一則預告

明年運籌優化領域的文章主題，偷偷預告一下，大概率是隨機優化和魯棒優化，即，模型輸入存在不確定性情況下的最優決策。

具體的學習路徑，我還沒思考清楚——當然了，即使已經想清楚了，我也不會直接公開出來，大概率會類似于這樣，等明年年底總結吧！

最后的最后，愿大家都能持之以恒地做一件件小事，慢慢努力，驚艷眾人。