第六章?句法制導翻譯概述
句法制導翻譯概述
什么是句法制導翻譯
編譯的階段:詞法分析→句法分析→語義分析→中間代碼生成→代碼優化→目標代碼生成
語義翻譯:語義分析和中間代碼生成
句法制導翻譯 :句法分析和語義分析和中間代碼生成
句法制導翻譯使用CFG來引導對語言的翻譯, 是一種面向文法的翻譯技術
句法制導翻譯的基本思想
如何表示語義信息?
- 為CFG中的文法符號設置語義屬性,用來表示語法成分對應的語義信息
如何計算語義屬性?
- 文法符號的語義屬性值是用與文法符號所在產生式(句法規則)相關聯的語義規則來計算的
- 對于給定的輸入串x ,構建x的句法分析樹,并利用與產生式(句法規則)相關聯的語義規則來計算分析樹中各結點對應的語義屬性值
兩個概念
將語義規則同句法規則(產生式)聯系起來要涉及兩個概念
- 句法制導定義(Syntax-Directed Definitions, SDD)
- 句法制導翻譯方案 (Syntax-Directed Translation Scheme , SDT )
句法制導定義(SDD)
SDD是對CFG的推廣
- 將每個文法符號和一個語義屬性集合相關聯
- 將每個產生式和一組語義規則相關聯,這些規則用于計算該產生式中各文法符號的屬性值

如果X是一個文法符號,a是X的一個屬性,則用X.a表示屬性a在某個標號為X的分析樹結點上的值
句法制導翻譯方案(SDT)
SDT是在產生式右部嵌入了程序片段的CFG,這些程序片段稱為語義動作。按照慣例,語義動作放在花括號內
例子
D → T { L.inh = T.type } L
T → int { T.type = int }
T → real { T.type = real }
L → { L1.inh = L.inh }L1, id ?? ? ?
?…
一個語義動作在產生式中的位置決定了這個動作的執行時間
SDD與SDT
SDD
- 是關于語言翻譯的高層次規格說明
- 隱蔽了許多具體實現細節,使用戶不必顯式地說明翻譯發生的順序
SDT
- 可以看作是對SDD的一種補充,是SDD的具體實施方案
- 顯式地指明了語義規則的計算順序,以便說明某些實現細節
句法制導定義SDD
句法制導定義SDD是對CFG的推廣
- 將每個文法符號和一個語義屬性集合相關聯
- 將每個產生式和一組語義規則相關聯,用來計算該產生式中各文法符號的屬性值
文法符號的屬性
- 綜合屬性 (synthesized attribute)
- 繼承屬性 (inherited attribute)
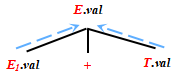
綜合屬性(synthesized attribute)
在分析樹結點 N上的非終結符A的綜合屬性只能通過 N的子結點或 N本身的屬性值來定義
例子:
產生式 ? ? ? ? ? ? ? ? ?語義規則
E → E1 + T ? ? ? E.val = E1.val + T.val
終結符可以具有綜合屬性。終結符的綜合屬性值是由詞法分析器提供的詞法值,因此在SDD中沒有計算終結符屬性值的語義規則。
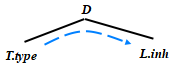
繼承屬性(inherited attribute)
在分析樹結點 N上的非終結符A的繼承屬性只能通過 N的父結點、N的兄弟結點或 N本身的屬性值來定義
例子:
產生式 ? ? ? ? ? ? 語義規則
D → T L ? ? ? L. inh = T. type
終結符沒有繼承屬性。終結符從詞法分析器處獲得的屬性值被歸為綜合屬性值?
例子:
帶有綜合屬性的SDD
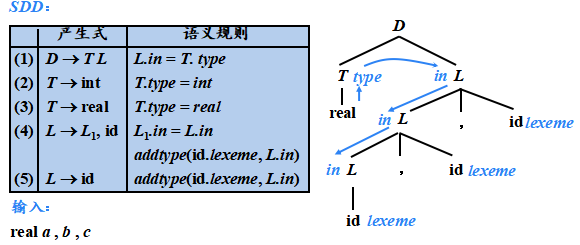
SDD:
輸入: 3*5+4n
注釋分析樹 ( Annotated parse tree ) : 每個節點都帶有屬性值的分析樹
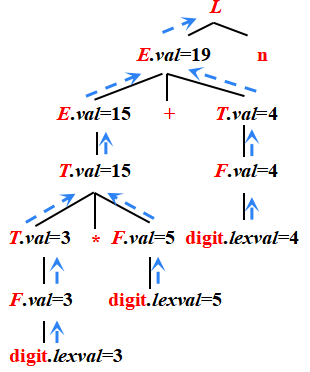
帶有繼承屬性L.in的SDD
SDD:

?輸入: real a , b , c
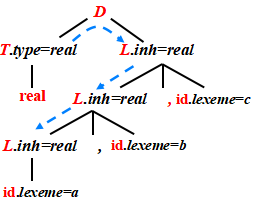
D → T L ? ? ? ? ? ?? (使用規則 1)
T → real? ? ? ? ? ? ?(使用規則 3)
L → L1 , id ? ? ? ? ?(使用規則 4)
L1 → L2 , id ? ? ? ?(再次使用規則 4)
L2 → id ? ? ? ? ? ? ? (使用規則 5)
屬性傳遞過程(也就是“語義規則”的作用)
1?? T → real:
T.type = real
2?? D → T L:
L.inh = T.type = real
3?? L → L1 , id(c):
L1.inh = L.inh = realaddtype("c", real)
4?? L1 → L2 , id(b):
L2.inh = L1.inh = realaddtype("b", real)
5?? L2 → id(a):
addtype("a", real)
最終效果:構建符號表
通過這些繼承屬性 + 語義動作,我們完成了:
符號表:
a : real
b : real
c : real
在這個例子中,T.type 是一個綜合屬性(自己決定),L.inh 是繼承屬性(從左邊的 T 傳來的類型信息),所有變量都通過 L.inh 拿到自己的類型,最后用 addtype(...) 加進符號表。
屬性文法 (Attribute Grammar)
一個沒有副作用的SDD有時也稱為屬性文法 (屬性文法的規則僅僅通過其它屬性值和常量來定義一個屬性值)
例子:

副作用指的是:一個操作除了計算返回值之外,還改變了外部狀態(比如內存、符號表、輸出等)。
常見的副作用包括:
改變一個變量的值(寫入內存)
修改符號表
打印輸出(如
print(...))執行文件或網絡操作
在 SDD(語法制導定義)中,副作用表現在哪?
在 SDD 中:如果一個語義規則只是用來計算屬性值,不對外部狀態造成影響,那就是無副作用的 SDD,也叫屬性文法(Attribute Grammar)。
有副作用的 SDD 舉例:
L → id
語義規則:addToSymbolTable(id.lexeme, type)這個規則調用了
addToSymbolTable(...),修改了符號表 ? 就是有副作用的。
SDD的求值順序
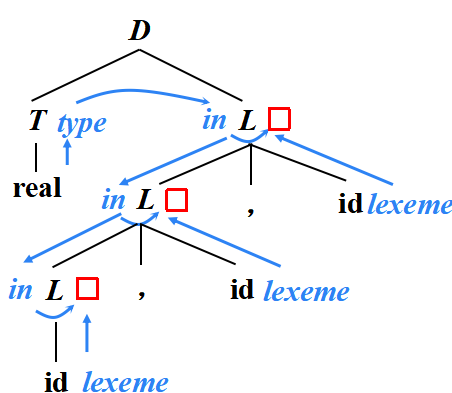
SDD為CFG中的文法符號設置語義屬性。對于給定的輸入串x,應用語義規則計算分析樹中各結點對應的屬性值
按照什么順序計算屬性值? 語義規則建立了屬性之間的依賴關系,在對句法分析樹節點的一個屬性求值之前,必須首先求出這個屬性值所依賴的所有屬性值
依賴圖(Dependency Graph)
依賴圖是一個描述了分析樹中結點屬性間依賴關系的有向圖
分析樹中每個標號為X的結點的每個屬性a都對應著依賴圖中的一個結點
如果屬性X.a的值依賴于屬性Y.b的值,則依賴圖中有一條從Y.b的結點指向X.a的結點的有向邊
例子
?如果一條語義規則的作用和求值無關,如打印一個值或向符號表中添加記錄,則成為生成式左側非終結符的虛擬綜合屬性。
常見的虛擬綜合屬性: ? ? ? ?
1)print(any) 打印any; ? ? ? ?
2)addtype(id.entry, type) 在符號表中為符號id添加符號類型(變量類型)type id.entry指明符號id在符號表中的入口
屬性值的計算順序?
可行的求值順序是滿足下列條件的結點序列N1, N2, … , Nk :如果依賴圖中有一條從結點Ni到 Nj 的邊(Ni→Nj), ?那么i < j(即:在節點序列中,Ni 排在Nj 前面)
這樣的排序將一個有向圖變成了一個線性排序,這個排序稱為這個圖的拓撲排序(topological sort)
例子
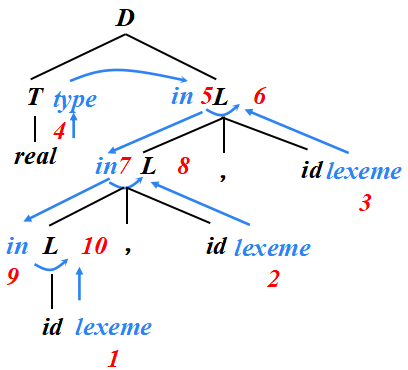
對于只具有綜合屬性的SDD ,可以按照任何自底向上的順序計算它們的值
對于同時具有繼承屬性和綜合屬性的SDD,不能保證存在一個順序來對各個節點上的屬性進行求值?
例子
產生式? ? ? 語義規則 ?
A→ B?? ? ? ? A.s = B.i
? ? ? ? ? ? ? ? ? ?B.i = A.s +1
如果圖中沒有環,那么至少存在一個拓撲排序
S-屬性定義與L-屬性定義
S-屬性定義
僅僅使用綜合屬性的SDD稱為S屬性的SDD,或S-屬性定義、S-SDD
例:

如果一個SDD是S屬性的,可以按照句法分析樹節點的任何自底向上順序來計算它的各個屬性值
S-屬性定義可以在自底向上的句法分析過程中實現
L-屬性定義
L-屬性定義(也稱為L屬性的SDD或L-SDD)的直觀含義:在一個產生式所關聯的各屬性之間,依賴圖的邊可以從左到右,但不能從右到左(因此稱為L屬性的,L是Left的首字母)
L-SDD的正式定義
一個SDD是L-屬性定義,當且僅當它的每個屬性要么是一個綜合屬性,要么是滿足如下條件的繼承屬性:假設存在一個產生式A→X1X2…Xn,其右部符號Xi (1<=?i <=?n)的繼承屬性僅依賴于下列屬性:
- A的繼承屬性
- 產生式中Xi左邊的符號 X1, X2, … , Xi-1 的屬性
- Xi本身的屬性,但Xi 的全部屬性不能在依賴圖中形成環路
每個S-屬性定義都是L-屬性定義
例子:L-SDD
L型 SDD:每個屬性的求值從左往右按順序就能完成,只依賴左邊的兄弟或父節點的信息。
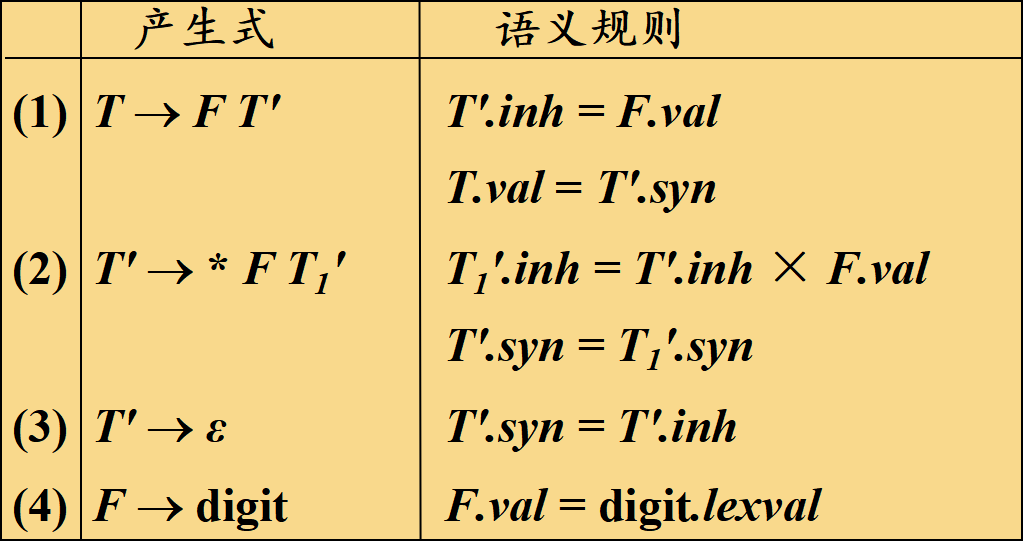
什么是綜合屬性(synthesized attributes)
->從子節點計算并“傳回”父節點的屬性值。下往上傳(由子決定父)
什么是繼承屬性(inherited attributes)
->是從父節點或左兄弟“傳遞給”當前節點的屬性值。從左往右傳(父兄決定子)
綜合屬性有:T.val、T′.syn、F.val
繼承屬性有:T′.inh、T1′.inh
非L屬性的SDD
L-屬性(L-attributed)SDD 是指:每個繼承屬性的值,只依賴于 父節點 和 左邊的兄弟節點的綜合屬性(syn)。
而如果一個 SDD 的屬性依賴了“右邊的兄弟”,那它就 不是 L 屬性的,叫做 非 L 屬性的 SDD,這類在自頂向下翻譯中不適用。
例子:

綜合屬性有:A.s
繼承屬性有:L.i、M.i、R.i、Q.i
句法制導翻譯方案SDT
句法制導翻譯方案(SDT )是在產生式右部中嵌入了程序片段(稱為語義動作)的CFG
SDT可以看作是SDD的具體實施方案 本節主要關注如何使用SDT來實現兩類重要的SDD,因為在這兩種情況下,SDT可在句法分析過程中實現
- 基本文法可以使用LR分析技術,且SDD是S屬性的
- 基本文法可以使用LL分析技術,且SDD是L屬性的
| 分析方式 | 能用的語法文法類型 | 配合的 SDD 類型 | 使用的 SDT 風格 |
|---|---|---|---|
| LL 分析器(自頂向下) | LL 文法 | L-屬性 SDD | 把語義動作插入在產生式右部的中間或前面 |
| LR 分析器(自底向上) | LR 文法 | S-屬性 SDD | 把語義動作插入在產生式右部的末尾 |
S 屬性(Synthesized)SDD:只有綜合屬性,從子節點傳上來的(適合 LR)
L 屬性(Left-attributed)SDD:屬性可以從左兄弟或父節點傳來(適合 LL)
將S-SDD轉換為SDT
將一個S-SDD轉換為SDT的方法:將每個語義動作都放在產生式的最后
例子:

S-屬性定義的SDT 實現
如果一個S-SDD的基本文法可以使用LR分析技術,那么它的SDT可以在LR句法分析過程中實現
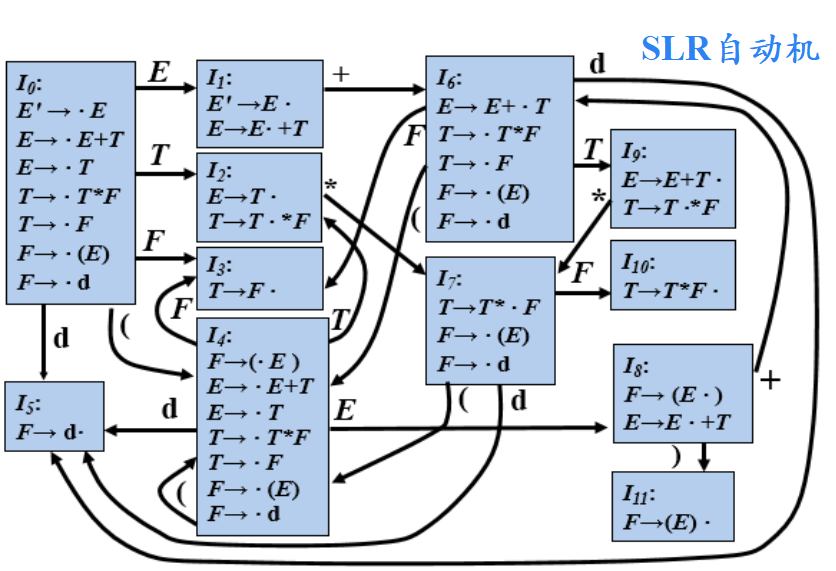
當歸約發生時執行相應的語義動作
?擴展的LR句法分析棧
在分析棧中使用一個附加的域來存放綜合屬性值
若支持多個屬性:使棧記錄變得足夠大;在棧記錄中存放指針
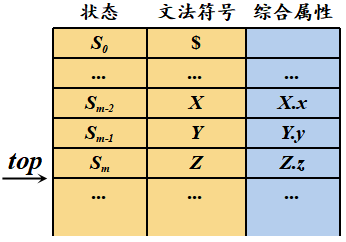
將語義動作中的抽象定義式改寫成具體可執行的棧操作
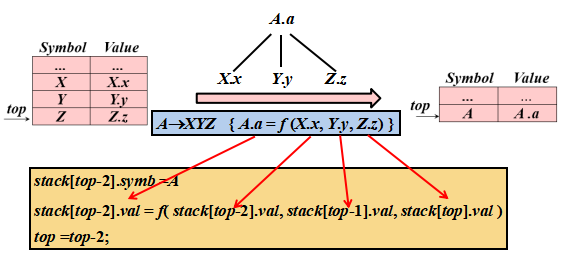
例子:
在自底向上句法分析棧中實現桌面計算器

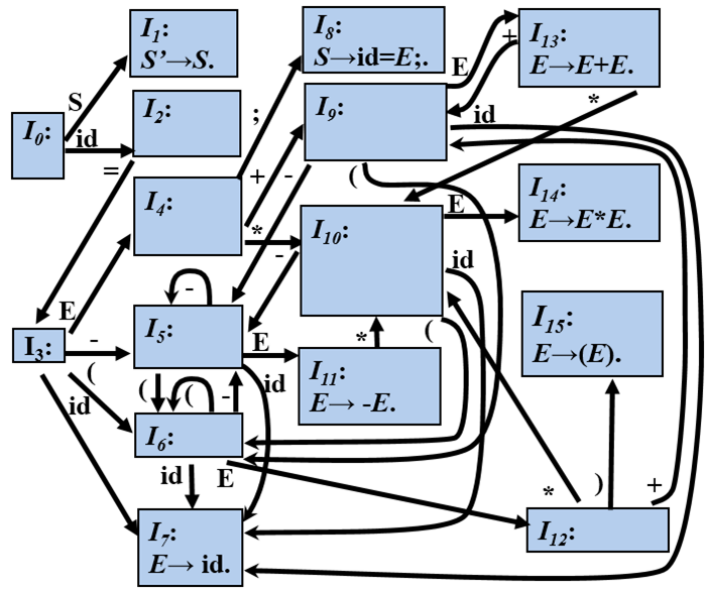
SLR自動機:
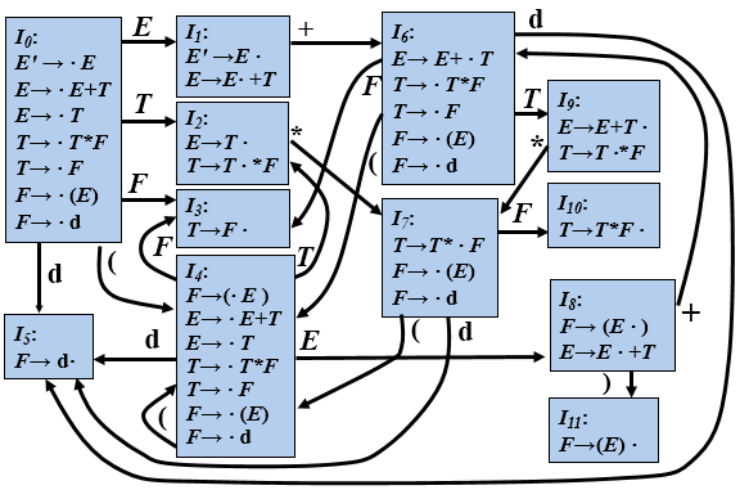
輸入: 3*5+4
將L-SDD轉換為SDT
將L-SDD轉換為SDT的規則
- 將計算某個非終結符號A的繼承屬性的動作插入到產生式右部中緊靠在A的本次出現之前的位置上
- 將計算一個產生式左部符號的綜合屬性的動作放置在這個產生式右部的最右端
例子
L-SDD

SDT
1) T → F { T′.inh = F.val } T′ { T.val = T′.syn }
2) T′ → *F { T1′.inh = T′.inh×F.val } T1′ { T′.syn = T1′.syn }
3) T′ → ε { T′.syn = T′.inh }
4) F → digit { F.val = digit.lexval }
L-屬性定義的SDT 實現
如果一個L-SDD的基本文法可以使用LL分析技術,那么它的SDT可以在LL或LR句法分析過程中實現
- 在非遞歸的預測分析過程中進行語義翻譯
- 在遞歸的預測分析過程中進行語義翻譯
- 在LR分析過程中進行語義翻譯
在非遞歸的預測分析過程中進行翻譯
擴展句法分析棧
例子
1) T → F { T′.inh = F.val } T′ { T.val = T′.syn }
2) T′ → *F { T1′.inh = T′.inh×F.val } T1′ { T′.syn = T1′.syn }
3) T′ → ε { T′.syn = T′.inh }
4) F → digit { F.val = digit.lexval }
轉為

分析棧中的每一個記錄都對應著一段執行代碼
- 綜合記錄出棧時,要將綜合屬性值復制給后面特定的語義動作(如果有需要)
- 變量展開時(即變量本身的記錄出棧時),如果其含有繼承屬性,則要將繼承屬性值復制給后面特定的語義動作(位于即將擴展的產生式右部)
例子

1) T → F {a1:T′.inh=F.val} T′ {a2:T.val=T′.syn}
符號 | 屬性 | 執行代碼 |
F | ||
Fsyn | val | stack[top-1].Fval?=?stack[top].val;top=top-1; |
a1 | Fval | stack[top-1].inh?=?stack[top].Fval;top=top-1; |
T′ | inh | 根據當前輸入符號選擇產生式進行推導 若選?2):?stack[top+3].T′inh?=stack[top].inh;??top=top+6; 若選?3):?stack[top].T′inh?=stack[top].inh;???? |
T′syn | syn | stack[top-1].T′syn?=?stack[top].syn;top=top-1; |
a2 | T′syn | stack[top-1].val?=?stack[top].T′syn;top=top-1; |
?2) T′ → *F{a3:T1′.inh=T′.inh×F.val}T1′{a4:T′.syn=T1′.syn}
符號 | 屬性 | 執行代碼 |
* | ||
F | ||
Fsyn | val | stack[top-1].Fval?=?stack[top].val;top=top-1; |
a3 | T?inh;?Fval | stack[top-1].inh?=?stack[top].T′inh×?stack[top].Fval;top=top-1; |
T1′ | inh | 根據當前輸入符號選擇產生式進行推導 若選2):?stack[top+3].T′inh?=?stack[top].inh;??top=top+6; 若選3):?stack[top].T′inh?=?stack[top].inh;???? |
T1′syn | syn | stack[top-1].T1′syn?=?stack[top].syn;top=top-1; |
a4 | T1′syn | stack[top-1].syn?=?stack[top].T1′syn;top=top-1; |
?3) T′ → ε {a5:T′.syn = T′.inh }
符號 | 屬性 | 執行代碼 |
a5 | T′inh | stack[top-1].syn?=?stack[top].T′inh; top=top-1; |
?4) F → digit {a6:F.val = digit.lexval}
符號 | 屬性 | 執行代碼 |
digit | lexval | stack[top-1].digitlexval?=?stack[top].lexval; top=top-1; |
a6 | digitlexval | stack[top-1].val?=?stack[top].digitlexval; top=top-1; |
輸入: 3 * 5?
在遞歸的預測分析過程中進行翻譯
算法
- 為每個非終結符A構造一個函數,A的每個繼承屬性對應該函數的一個形參,函數的返回值是A的綜合屬性值。對出現在A產生式中的每個文法符號的每個屬性都設置一個局部變量 ?
- 非終結符A的代碼根據當前的輸入決定使用哪個產生式
與每個產生式有關的代碼執行如下動作:
從左到右考慮產生式右部的詞法單元、非終結符及語義動作 ?
- 對于帶有綜合屬性x的詞法單元 X,把x的值保存在局部變量X.x中;然后產生一個匹配 X的調用,并繼續輸入
- 對于非終結符B,產生一個右部帶有函數調用的賦值語句c := B(b1 , b2 , …, bk),其中, b1 , b2 , …, bk是代表B的繼承屬性的變量,c是代表B的綜合屬性的變量
- 對于每個動作,將其代碼復制到句法分析器,并把對屬性的引用改為對相應變量的引用
?例子:
SDT
1) T → F { T′.inh = F.val } T′ ?? ?{ T.val = T′.syn }
2) T′ → *F { T1′.inh = T′.inh×F.val } T1′ ?{ T′.syn = T1′.syn }
3) T′ → ε { T′.syn = T′.inh }
4) F → digit { F.val = digit.lexval }
T′syn T′ (token, T′inh)
//為每個非終結符A構造一個函數,A的每個繼承屬性對應該函數的一個形參,函數的返回值是A的綜合屬性值
{ ?
? ? D: Fval, T1′inh, T1′syn;
//對出現在A產生式右部中的每個文法符號的每個屬性都設置一個局部變量
? ? if token=“*” ?then
? ? { ?Getnext(token);
?? ? ? Fval=F(token);
?? ? ? T1′inh= T′inh×Fval;
?? ? ? Getnext(token);
?? ? ? T1′syn=T1′(token, T1′inh);
?? ? ? T?syn=T1′syn;
?? ? ? return T′syn;
? ? ?}
?? ?else if token= “ $” then
? ? ?{ ?
? ? ? T′syn= T′inh;
?? ? ? return T′syn;
? ? ?}
//
? ? ?else Error;
}
L-屬性定義的自底向上翻譯
給定一個以LL文法為基礎的L-SDD,可以修改這個文法,并在LR句法分析過程中計算這個新文法之上的SDD
( 原本設計為 LL 分析 + L-屬性 SDD 的程序,只要重寫文法 + 插入中間動作(@pass),
就可以變成適用于 LR 分析的 SDT 實現方式。)
| 概念 | 解釋 |
|---|---|
| LL 文法 | 左到右,自頂向下,預測式分析(用棧+遞歸下降) |
| LR 文法 | 左到右,自底向上,歸約式分析(更強大但更復雜) |
| L-屬性 SDD | 屬性可以依賴于父親和左邊兄弟的信息(適合 LL 分析) |
| S-屬性 SDD | 屬性只能從孩子傳上來(適合 LR 分析) |
?例子
1) T → F { T′.inh = F.val } T′ { T.val = T′.syn }
2) T′ → *F { T1′.inh = T′.inh×F.val } T1′ { T′.syn = T1′.syn }
3) T′ → ε { T′.syn = T′.inh }
4) F → digit { F.val = digit .lexval }
這是一個典型的 LL 分析 + L 屬性 SDD 的寫法:
| 繼承屬性 | T′.inh、T1′.inh |
|---|---|
| 綜合屬性 | F.val、T′.syn、T.val 等 |
重點問題是:
繼承屬性 T′.inh = F.val 是要在處理 T′ 之前就先計算的
所以只能在 LL 分析中執行
LR 分析器是歸約式,不能在中間執行動作,所以我們引入中間產生式來提前執行語義動作
變成:修改后的SDT,所有語義動作都位于產生式末尾
1) T → F M T′ ? ? ? ? ? ? { T.val = T′.syn }
2) M → ε ? ? ? ? ? ? ? ? ?{ M.i = F.val; M.s = M.i }
3) T′ → * F N T1′ ? ? ? ? { T′.syn = T1′.syn }
4) N → ε ? ? ? ? ? ? ? ? ?{ N.i1 = T′.inh; N.i2 = F.val; N.s = N.i1 × N.i2 }
5) T′ → ε ? ? ? ? ? ? ? ? { T′.syn = T′.inh }
6) F → digit ? ? ? ? ? ? ?{ F.val = digit.lexval }
T → F M T′ ? ? ? ? ? ? ? { T.val = T′.syn }
M → ε ? ? ? ? ? ? ? ? ? { M.i = F.val; M.s = M.i }
引入了中間符號
M,讓M → ε的動作在F之后、T′之前執行利用
M計算F.val,保存起來供T′使用在 LR 歸約中,我們可以先歸約
F、然后歸約M,就能保證F.val在T′用之前被計算T′ → * F N T1′ ? ? ? ? ?{ T′.syn = T1′.syn }
N → ε ? ? ? ? ? ? ? ? ? { N.i1 = T′.inh; N.i2 = F.val; N.s = N.i1 × N.i2 }
插入了 N → ε,把中間繼承計算提早執行
N.s實際上就是T1′.inh如果你愿意,后續還可以寫
T1′.inh = N.s,或者直接把N.s傳給T1′
T′ → ε ? ? ? ? ? ? ? ? ?{ T′.syn = T′.inh }
F → digit ? ? ? ? ? ? ? { F.val = digit.lexval }
| 原來 | 現在 | 為什么要改 |
|---|---|---|
T′.inh = F.val | M → ε { M.i = F.val } | 提前在 LR 中執行語義動作 |
T1′.inh = T′.inh × F.val | N → ε { 計算 N.s } | 提前傳值給 T1′ |
| 繼承屬性(inh) | 臨時變量中間保存 | LR 無法中途插入動作 |
我們要把SDT 中的語義動作 {} 替換成文法中的“標記非終結符”(dummy symbol),這樣就可以用 LR 分析器來處理這些語義動作了
把這種形式A → α {a} β
變成這種形式:
A → α M β
M → ε ? // 把原來的動作 a 放到 M 這個產生式里去
- 首先構造SDT,在各個非終結符之前放置語義動作來計算它的繼承屬性, 并在產生式后端放置語義動作計算綜合屬性
每當想計算一個繼承屬性,就把語義動作
{}放在它前面每當想計算一個綜合屬性,就把語義動作
{}放在它后面
- 對每個內嵌的語義動作,向文法中引入一個標記非終結符來替換它。每個這樣的位置都有一個不同的標記,并且對于任意一個標記M都有一個產生式M→ε
例如這條產生式:T → F { T′.inh = F.val } T′ { T.val = T′.syn }
我們就加兩個標記符號
M1和M2,變成:T → F M1 T′ M2然后加兩個新產生式:
M1 → ε ? ? ? // 執行 { T′.inh = F.val }
M2 → ε ? ? ? // 執行 { T.val = T′.syn }
每個
{}都變成不同的M1,M2,M3...每個
Mi都是一個產生式Mi → ε,但它背后執行的是原來的動作
- 如果標記非終結符M在某個產生式A→α{a}β中替換了語義動作a,對a進行修改得到a' ,并且將a'關聯到M→ε 上。動作a'
把
{a}拆出去,扔到M → ε里去執行
a'其實和a做的是一回事,只是你要明確它用到哪些繼承/綜合屬性
- (a) 將動作a需要的A或α中符號的任何屬性作為M的繼承屬性進行復制
假如原來寫的是:
T′.inh = F.val那現在
M1 → ε這個動作,就要通過M1.i = F.val來模擬繼承傳值換句話說:把
F.val傳給M1的繼承屬性
- (b) 按照a中的方法計算各個屬性,但是將計算得到的這些屬性作為M的綜合屬性
原來
{ T′.inh = F.val }是在產生式中直接執行現在你要在
M1 → ε這個動作中執行它所以結果比如
M1.s = F.val(綜合屬性),后續由M1.s傳給T′.inh
將語義動作改寫為可執行的棧操作
例子:
1) T → F M T′ ? ? ? ? ? ? { T.val = T′.syn }
2) M → ε ? ? ? ? ? ? ? ? ?{ M.i = F.val; M.s = M.i }
3) T′ → * F N T1′ ? ? ? ? { T′.syn = T1′.syn }
4) N → ε ? ? ? ? ? ? ? ? ?{ N.i1 = T′.inh; N.i2 = F.val; N.s = N.i1 × N.i2 }
5) T′ → ε ? ? ? ? ? ? ? ? { T′.syn = T′.inh }
6) F → digit ? ? ? ? ? ? ?{ F.val = digit.lexval }
1)
T→F M T′ {stack[top-2]. val = stack[top].syn; top = top-2;} ? ? ?
M→ ε {stack[top+1]. s = stack[top].val; top = top+1;} ?? ?
2)
T′→*F N T1′ {stack[top-3]. syn = stack[top].syn; top = top-3;}
N → ε {stack[top+1]. s = stack[top-2]. s × stack[top].val; top = top+1;}
3)
T′→ε{stack[top+1].syn = stack[top]. s; top = top+1;}
4)
F →digit {stack[top].val = stack[top]. lexval;}
例子

第七章 中間代碼生成
類型表達式
基本類型是類型表達式
- integer
- real
- char
- boolean
- type_error (出錯類型)
- void (無類型)
可以為類型表達式命名,類型名也是類型表達式
將類型構造符(type constructor)作用于類型表達式可以構成新的類型表達式
例如:
(1)數組構造符array
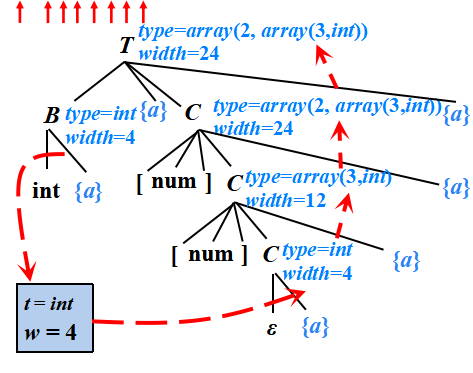
若T是類型表達式,則array ( I, T )是類型表達式( I是一個整數)
類型 | 類型表達式 |
int?[3] | array?(3,?int?) |
int?[2][3] | array?(2,?array(3,int)?)? |
?(2)指針構造符pointer
若T 是類型表達式,則 pointer ( T ) 是類型表達式,它表示一個指針類型
(3)笛卡爾乘積構造符×
若T1 和T2是類型表達式,則笛卡爾乘積T1 × T2 是類型表達式
(4)函數構造符
若T1、T2、…、Tn 和R是類型表達式,則T1×T2 ×…×Tn→ R是類型表達式
(5)記錄構造符record
若有標識符N1 、N2 、…、Nn 與類型表達式T1 、T2 、…、Tn , 則 ? ? record ( ( N1 ?× T1 ) × ( N2 × T2 )× …× ( Nn × Tn )) 是一個類型表達式
例子
設有C程序片段
struct ? stype ?? ??? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
{ ? char[8] name;
? ??int ?score; ?? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
}; ?? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
stype[50] table; ?? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
stype* p;
- 和stype綁定的類型表達式:record ( (name× array(8, char)) × (score × integer) )
- 和table綁定的類型表達式 :array (50, stype)
- 和p綁定的類型表達式 :pointer (stype)
聲明語句的翻譯
局部變量的存儲分配
對于聲明語句,語義分析的主要任務就是收集標識符的類型等屬性信息,并為每一個名字分配一個相對地址
- 從類型表達式可以知道該類型在運行時刻所需的存儲單元數量稱為類型的寬度(width)
- 在編譯時刻,可以使用類型的寬度為每一個名字分配一個相對地址
名字的類型和相對地址信息保存在相應的符號表記錄中
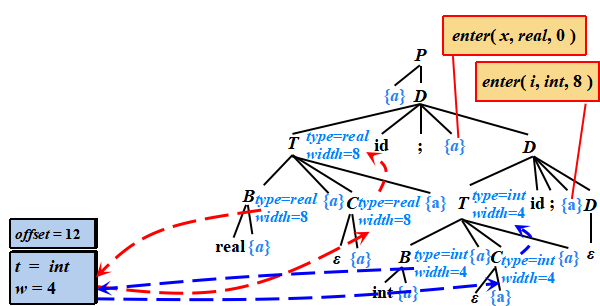
變量聲明語句的SDT
enter( name, type, offset ):在符號表中為名字name創建記錄,將name的類型設置為type,相對地址設置為offset
例子
① P →{ offset = 0 } D
② D → T id;{ enter( id.lexeme, T.type, offset ); offset = offset + T.width; }D
③ D → ε
④ T → B ? { t =B.type; w=B.width;}? C ? { T.type = C.type; T.width = C.width; }
⑤ T → ↑T1{ T.type = pointer( T1.type); T.width = 4; }
⑥ B → int { B.type = int; B.width = 4; }
⑦ B → real{ B.type = real; B.width = 8; }
⑧ C → ε ?{ C.type=t; C.width=w; }
⑨ C → [num]C1 { C.type = array( num.val, C1.type);? ?C.width = num.val * C1.width; }
符號 | 綜合屬性 |
B? | type,?width |
C | type,?width |
T | type,?width |
變量 | 作用 |
offset | 下一個可用的相對地址 |
t,?w | 將類型和寬度信息從語法分析樹中的B結點傳遞到對應于產生式C?→ε的結點 |
?“real x; int i;”的語法制導翻譯
?類型表達式“int[2][3]”的語法制導翻譯
中間代碼的形式
四元式是一種“三地址語句”的等價表示。它的一般形式為:(op,arg1,arg2,result)
其中,op為一個二元(也可是一元或零元)運算符; arg1,arg2分別為它的兩個運算對象,它們可以是變量、常數或系統定義的臨時變量名;運算的結果將放入result中。
四元式還可寫為類似于PASCAL語言的賦值語句的形式:result := arg1 op arg2
四元式的格式
每個四元式只能有一個運算符,所以,一個復雜的表達式只能由多個四元式構成的序列表示。
例如,表達式A+B*C可寫為序列 ?? ?
T1:=B*C ??
T2:=A+T1
當op為一元、零元運算(如無條件轉移),arg2甚至arg1應缺省,即result:=op arg1或 op result ;對應的一般形式為:? (op,arg1,-,result) 或? (op,-,-,result) 。
三元式的格式
為了節省臨時變量的開銷,有時也可采用一種三元式結構來作為中間代碼,其一般形式為
(i) (op,arg1,arg2) ?? ?
其中,(i)為三元式的編號,也代表了該式的運算結果;op,arg1,arg2的含義與四元式類似,區別在于arg可以是某三元式的序號,表示用該三元式的結果作為運算對象。
例如,對于賦值語句a:=-b*(c+d),若用三元式表示,則可寫成 ?? ???
?①?? ??? ?(U_minus, ?b, ? - ?)? ? ? ?
?②?? ??? ?( ?+ ? , ? ? c, ? ?d ?) ?? ??? ?
③?? ??? ?( ?* ? ?, ? ? ①, ?② ) ?? ??? ?
④?? ??? ?( ?:= ?,?? ? ?③,?? ?a ?)
式①中的運算符U_minus表示一元減運算。
逆波蘭表示
每一運算符都置于其運算對象之后,故稱為后綴表示。
特點:表達式中各個運算是按運算符出現的順序進行的,無須使用括號來指示運算順序,因而又稱為無括號式。
例子
中綴表示?? ??? ??? ? ??后綴表示
A+B?? ??? ??? ??? ? ? ? ? AB+
A+B*C?? ??? ??? ? ? ? ? ABC*+
(A+B)*(C+D)?? ??? ? ?AB+CD+
* x/y^z-d*e?? ??? ? ? ? ?xyz^/de*-
| 運算符 | 含義 | 優先級 | 結合性 |
|---|---|---|---|
^ | 冪 | 最高 | 右結合 |
* / | 乘除 | 中等 | 左結合 |
+ - | 加減 | 最低 | 左結合 |
?例子:
中綴:x / y ^ z - d * e
最終后綴表達式為:x y z ^ / d e * -
| 當前位置 | 操作 | 棧(top→bottom) | 輸出結果 |
|---|---|---|---|
x | 輸出 | x | |
/ | 壓棧 | / | x |
y | 輸出 | / | x y |
^ | 壓棧(比 / 高) | ^ / | x y |
z | 輸出 | ^ / | x y z |
- | 比較棧頂 ^ → 彈出 ^ | / | x y z ^ |
比較 - vs / → 彈出 / | 空 | x y z ^ / | |
壓入 - | - | x y z ^ / | |
d | 輸出 | - | x y z ^ / d |
* | 優先級比 - 高,壓棧 | * - | x y z ^ / d |
e | 輸出 | * - | x y z ^ / d e |
| END | 彈出 *, - | x y z ^ / d e * - |
簡單賦值語句的翻譯
賦值語句翻譯的任務
賦值語句的基本文法
① S → id = E;
② E → E1 + E2 ?
③ E → E1 * E2 ?
④ E →?-E1 ?? ? ?
⑤ E → (E1) ?
⑥ E → id
賦值語句翻譯的主要任務:生成對表達式求值的三地址碼
例子:
源程序片段 x = ( a + b ) * c ;
三地址碼 t1 = a + b;t2 = t1 * c;x ?= t2
賦值語句的SDT
lookup(name):查詢符號表返回name 對應的記錄
gen(code):生成三地址指令code
newtemp( ):生成一個新的臨時變量t,返回t的地址
例子:a = b + c * d;
生成:
t1 = c * d
t2 = b + t1
a = t2
S → id = E;
{ p = lookup(id.lexeme); if p == nil then error ;? S.code = E.code ||? ?gen( p ‘=’ E.addr ); }
這里的
||不是邏輯或運算符,而是表示“代碼的連接/拼接”,意思是把兩段中間代碼拼成一段完整的中間代碼。(把表達式 E 的代碼,接在前面,再加上一句p = E.addr,合成S.code)
id = E是賦值語句,例如a = b + c;
lookup(id.lexeme)查找變量a是否已聲明如果
a沒有聲明 → 報錯
E.code是表達式右邊的代碼(可能是好幾條)
E.addr是表達式的最終結果(臨時變量或變量地址)
gen(p = E.addr)→ 生成最終賦值語句:a = t2
E → E1 + E2
{ E.addr = newtemp( );? ? E.code = E1.code || E2.code||? ?gen(E.addr ‘=’ E1.addr ‘+’ E2.addr); }
生成新臨時變量
t拼接左右兩邊的中間代碼
E1.code || E2.code然后再生成一條新代碼:
t = E1 + E2最后把結果地址保存在
E.addr
b + t1
→ t2 = b + t1
E → E1 * E2
{ E.addr = newtemp( );? ? ?E.code = E1.code || E2.code ||? gen(E.addr ‘=’ E1.addr ‘*’ E2.addr); }
c * d
→ t1 = c * d
E → -E1 ??
?{ E.addr = newtemp( );? E.code = E1.code||? ?gen(E.addr ‘=’ ‘uminus’ E1.addr); }
E → (E1)
{ E.addr = E1.addr;? E.code= E1.code;}
E → id ? ?? ?
{ E.addr = lookup(id.lexeme); if E.addr == nil then error ;? ? E.code = ‘’;}
增量翻譯 (Incremental Translation)
在增量方法中,gen( )不僅要構造出一個新的三地址指令,還要將它添加到至今為止已生成的指令序列之后
例子
例:x = ( a + b ) * c ;?
數組引用的翻譯
賦值語句的基本文法 ?? ?
S → id = E; | L = E; ?? ?
E→ E1 + E2 | -E1 ? | (E1) | id | L ??
?L→ id [E] | L1 [E]
數組引用翻譯成三地址碼時要解決的主要問題是確定數組元素的存放地址,也就是數組元素的尋址
數組元素尋址 (Addressing Array Elements )
一維數組
假設每個數組元素的寬度是w,則數組元素a[i]的相對地址是: ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
base+i×w ? ?
其中,base是數組的基地址,i×w是偏移地址
二維數組
假設一行的寬度是w1,同一行中每個數組元素的寬度是w2,則數組元素a[i1] [i2]的相對地址是: ?
base+i1×w1+i2×w2
k維數組
數組元素a[i1] [i2] …[ik]的相對地址是: ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
?base+i1×w1+i2×w2+…+ik×wk
w1 →a[i1] 的寬度;w2 →a[i1] [i2] 的寬度;… wk →a[i1] [i2] …[ik]的寬度
例子
假設type(a)= array(3, array(5, array(8, int) ) ), 一個整型變量占用4個字節, ? ?
則addr(a[i1][i2][i3]) = base + i1 * w1 ?+ i2*w2 + i3*w3? = base + i1*160 + i2*32 + i3*4
a[i1]的寬度:160;a[i1][i2]的寬度:32;a[i1][i2][i3]的寬度:4;
帶有數組引用的賦值語句的翻譯
例子1
假設 type(a)=array(n, int)
?源程序片段 ?c = a[i];
三地址碼
?t1 ?= i * 4 ? ?
?t2 ?= a [ t1 ] ?
c ? = t2
addr(a[i]) = base + i*4
例子2
假設 type(a)= array(3, array(5, int)),
源程序片段 ?c =a[i1][i2];
三地址碼
t1 = i1 * 20 ? ? ? ?
t2 = i2 * 4 ? ? ? ?
t3 = t1 + t2 ? ? ? ?
t4 ?= a [ t3 ] ? ? ? ?
c ? = ?t4
addr(a[i1][i2])= base + i1*20 + i2*4
數組引用的SDT
賦值語句的基本文法 ?? ?
S → id = E; | L = E; ?? ?
E → E1 + E2 | -E1 | (E1) | id | L ?? ?
L → id [E] | L1 [E]
?base+i1×w1+i2×w2+…+ik×wk
假設 type(a)= array(3, array(5, array(8, int) ) ),翻譯語句片段“a[i1][i2][i3]”

L的綜合屬性:
- L.type:L生成的數組元素的類型
- L.offset:指示一個臨時變量,該臨時變量用于累加公式中的ij × wj項,從而計算數組引用的偏移量
- L.array:數組名在符號表的入口地址

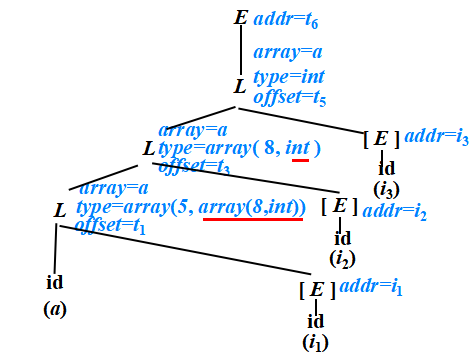
三地址碼 :t1 = i1*160 ;t2 = i2*32; t3 = t1+t2; t4 = i3*4; t5 = t3+t4 ;t6 = a[t5]
控制流語句及其SDT
控制流語句的基本文法
P → S
S →S1 S2
S →id = E ; | L = E ;?? ? ?
S → if B then S1
?? ??? ?| if B then S1 else S2
?? ??? ?| while B do S1
控制流語句的代碼結構
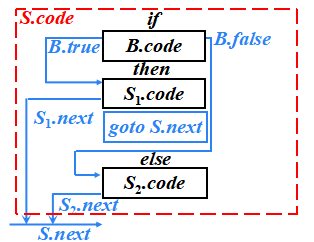
例子:S → if B then S1 else S2
布爾表達式B被翻譯成由跳轉指令構成的跳轉代碼
繼承屬性
- S.next:是一個地址,該地址中存放了緊跟在S代碼之后的指令(S的后繼指令)的標號
- B.true:是一個地址,該地址中存放了當B為真時控制流轉向的指令的標號
- B.false:是一個地址,該地址中存放了當B為假時控制流轉向的指令的標號
用指令的標號標識一條三地址指令
控制流語句的SDT
newlabel( ): 生成一個用于存放標號的新的臨時變量L,返回變量地址
label(L): 將下一條三地址指令的標號賦給L
P → { S.next = newlabel(); }S{ label(S.next);}
S →{ S1.next = newlabel(); }S1 { label(S1.next); S2.next= S.next ; }S2
S →id = E ; | L = E ;?? ? ?
S → if B then S1
?? ??? ?| if B then S1 else S2
?? ??? ?| while B do S1
if-then-else語句的SDT
S → if B then S1 else S2
S → if ?{ B.true = newlabel(); B.false = newlabel(); }?B
? ? ? ? then { label(B.true); S1.next = S.next; }?S1?{ gen( ‘goto’ ?S.next ) }
? ? ? ? else { label(B.false); S2.next = S.next; }S2

if-then語句的SDT
S → if B then S1
S → if { B.true = newlabel(); B.false = S.next; } B
? ? ? ? then { label(B.true); S1.next = S.next; } S1
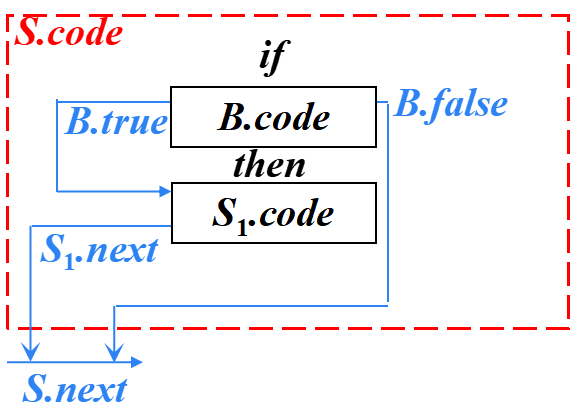
?while-do語句的SDT
S →while B do S1
S →while ?{S.begin = newlabel(); ?label(S.begin); ?B.true = newlabel(); ??B.false = S.next;}B
? ? ? ?do { label(B.true); S1.next = S.begin;} S1? { gen(‘goto’ S.begin); }
布爾表達式及其SDT
?? ?B → B or B
?? ??? ? ? | B and B
?? ??? ? ? | not B
?? ??? ? ? | (B)
?? ??? ? ? | E relop E
?? ??? ? ? | true
?? ??? ? ? | false
優先級:not > and > or
E relop E 是關系表達式
relop(關系運算符): <, ?<=, >, ?>=,==, ?! =
在跳轉代碼中,邏輯運算符&&、|| 和 ! 被翻譯成跳轉指令。運算符本身不出現在代碼中,布爾表達式的值是通過代碼序列中的位置來表示的
例子:
語句 : if ( x<100 || x>200 && x!=y ) ?? x=0;
三地址代碼:
? ? ? ? ? ?if x<100 goto L2
? ? ? ? ? ?goto L3
L3 : ?? ?if x>200 goto L4
? ? ? ? ? ?goto L1
L4 : ?? ?if x!=y goto L2 ??
? ? ? ? ? ? goto L1 ? ?
L2 :?? ?x=0 ? ? ?
L1 :
布爾表達式的SDT
B → E1 relop E2{ gen(‘if ’ E1.addr relop E2.addr ‘goto’ ?B.true);gen(‘goto’ B.false); }? ??
B → true ?{ gen(‘goto’ B.true); } ?
B → false ?{ gen(‘goto’ B.false); } ? ? ?
B → ( {B1.true =B. true; ?B1.false =B.false; } B1 )
B → not { B1.true = B.false; B1.false = B.true; } B1 ? ?
B → B1 or B2 ?的SDT
B → ?{ B1.true = B.true; ?B1.false = newlabel(); } B1
? ? ? ?or { label(B1.false); ?B2.true = B.true; ?B2.false = B.false; }B2 ?
B → B1 or B2 ?
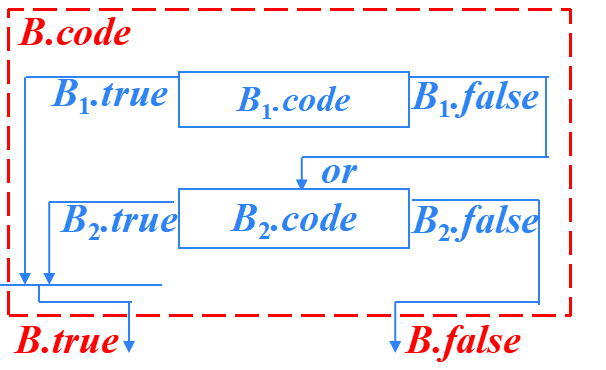
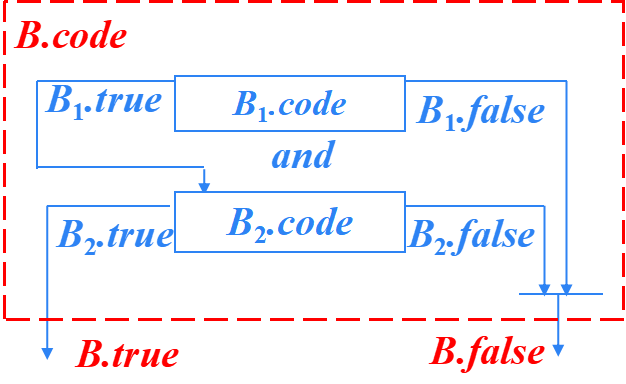
B → B1 and B2 ?的SDT
B → B1 and B2 ?
B → { B1.true = newlabel(); B1.false = B.false; }? B1
? ? ? ? ?and { label(B1.true); B2.true = B.true; B2.false = B.false; }B2?
控制流翻譯的例子
控制流語句的SDT
P → {a}S{a}
S → {a}S1{a}S2
S → id=E;{a} | L=E;{a}?? ? ?
E → E1+E2{a} | -E1{a} | (E1){a}| id{a}| L{a}
L → id[E]{a} | L1[E]{a}
S → if {a}B then {a}S1
? ? ? ? ? | if {a}B then {a}S1 else {a}S2
? ? ? ? ? | while {a}B do {a}S1{a}
B → {a}B or {a}B | {a}B and {a}B | not {a}B | ({a}B)
? ? ? ? ? | E relop E{a} | true{a} | false{a}
SDT的通用實現方法
任何SDT都可以通過下面的方法實現
首先建立一棵語法分析樹,然后按照從左到右的深度優先順序來執行這些動作
例子
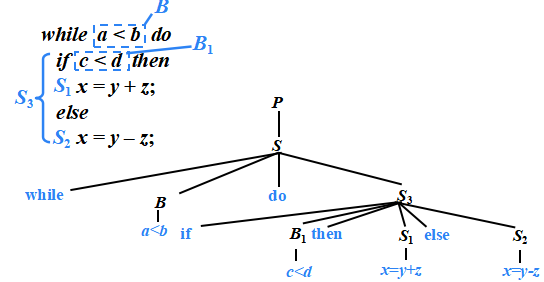
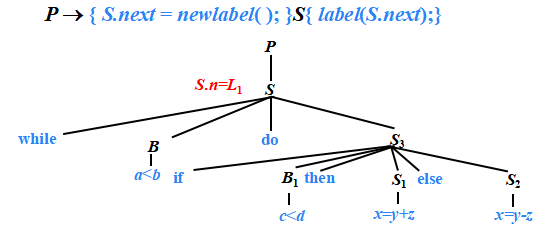
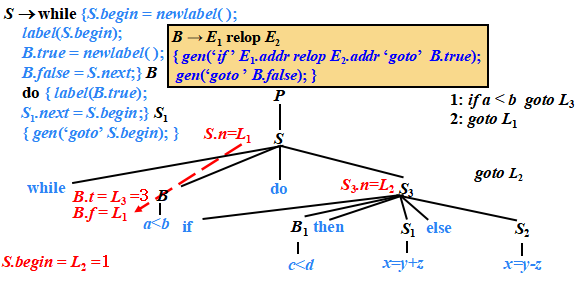
?語句“while a<b do if c<d then x=y+z ?else x=y-z”的三地址代碼
1: if a < b ?goto 3? ? ? ? ? ? ? ? ? 1: ( j<, ?a, ?b , ?3 )
2: goto 11? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 2: ( ?j , ?- , ?- , 11 )
3: if c < d ?goto 5? ? ? ? ? ? ? ? ? 3: ( j<, ?c, ?d , ?5 )
4: goto 8? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?4: ( ?j , ?- , ?- , ?8 )
5: t1 = y + z? ? ? ? ? ? ? ? ? ? ? ? ? 5: ( + , ?y , z , ?t1 ?)?
6: x = t1? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 6: ( = , ?t1, ?- , ?x )
7: goto 1? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?7: ( ?j , ?- , ?- , ?1 )
8: t2 = y - z? ? ? ? ? ? ? ? ? ? ? ? ? ?8: ( ?- , ?y, ?z , ?t2 )
9: x = t2? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?9: ( = , ?t2, ?- , ?x )
10: goto 1? ? ? ? ? ? ? ? ? ? ? ? ? ? ?10: ( ?j , ?- , ?- , ?1 )
11:? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 11:?
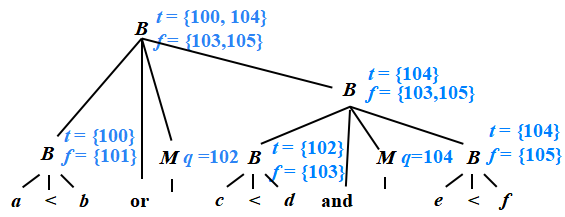
布爾表達式的回填
回填
基本思想:生成一個跳轉指令時,暫時不指定該跳轉指令的目標標號。這樣的指令都被放入由跳轉指令組成的列表中。同一個列表中的所有跳轉指令具有相同的目標標號。等到能夠確定正確的目標標號時,才去填充這些指令的目標標號。
非終結符B的綜合屬性
B.truelist:指向一個包含跳轉指令的列表,這些指令最終獲得的目標標號就是當B為真時控制流應該轉向的指令的標號
B.falselist:指向一個包含跳轉指令的列表,這些指令最終獲得的目標標號就是當B為假時控制流應該轉向的指令的標號
函數
- makelist( i ) 創建一個只包含i的列表,i是跳轉指令的標號,函數返回指向新創建的列表的指針
- merge( p1, p2 ) 將 p1 和 p2 指向的列表進行合并,返回指向合并后的列表的指針
- backpatch( p, i ) 將 i 作為目標標號插入到 p所指列表中的各指令中
布爾表達式的回填
B → E1 relop E2
B→ E1 relop E2 {
??? ?B.truelist = makelist(nextquad);
? ? ?B.falselist = makelist(nextquad+1);
??? ?gen(‘if ’ E1.addr relop E2.addr ‘goto _’);
??? ?gen(‘goto _’);
}
這段代碼是為了給布爾表達式生成“如果為真/為假跳到哪里”的中間代碼,它用的是延遲填充跳轉地址(回填技術)。你可以先生成跳轉語句,把地址留空,后面再統一填入真實目標。
表達式是:B -> E1 relop E2
表示布爾表達式 B 是兩個表達式 E1 和 E2 之間的關系運算(例如 <, ==, >= 等)。
B.truelist = makelist(nextquad);
B.truelist:布爾表達式為真的跳轉目標位置列表。makelist(nextquad):創建一個列表,里面是當前要生成的下一條指令的編號(因為這條指令就是當表達式為真時跳轉的地方)。- 作用:先占個位置,等確定真正跳轉到哪時再回填。
B.falselist = makelist(nextquad+1);
- 同理,這里是創建布爾表達式為假時的跳轉列表,是下一條指令之后的那條(即下一條是
if,再下一條是goto)。 - 也是先占位,等以后知道“跳哪里”再填進去。
gen(‘if ’ E1.addr relop E2.addr ‘goto _’);
生成條件跳轉語句,例如:if a < b goto _?
下劃線 _ 表示“回填位置”,現在不知道跳到哪里,就先留空。
gen(‘goto _’);
如果條件不滿足,就執行這個跳轉,也要回填:goto _
整體例子:
假設我們要處理:a < b
生成如下偽代碼:
(100) if a < b goto _
(101) goto _此時:
B.truelist = [100]
B.falselist = [101]
等你知道應該跳到哪兒時,比如:如果為真跳到 120 行,為假跳到 130 行,你就把
_回填成:(100) if a < b goto 120
(101) goto 130
?B → true
B → true { ?? ?
? ? ?B.truelist = makelist(nextquad); ??? ?
? ? ?gen(‘goto _’);
}
?B → false
?B → false {
?? ?B.falselist = makelist(nextquad);
??? ?gen(‘goto _’);
}
?B →(B1)
B→ (B1) {
?? ?B.truelist = B1.truelist ;
??? B.falselist = B1.falselist ;
}
B→ not B1?
?B → not B1 {
?? ?B.truelist = B1.falselist;
??? B.falselist = B1.truelist;
}
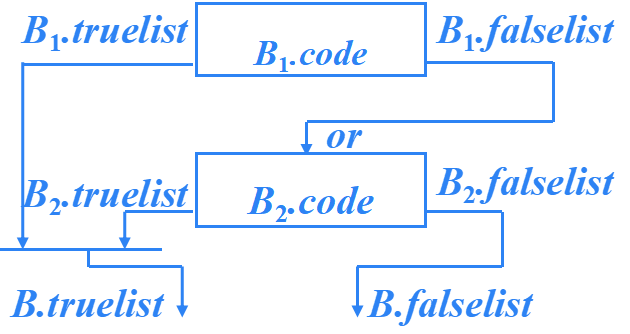
B → B1 or B2
?B → B1 or M B2 {
??? ?backpatch(B1.falselist, M.quad ); ?
?? ?B.truelist= merge(B1.truelist,B2.truelist );
??? ?B.falselist = B2.falselist ;
}
M → ε {?
? ?M.quad = nextquad ;
}
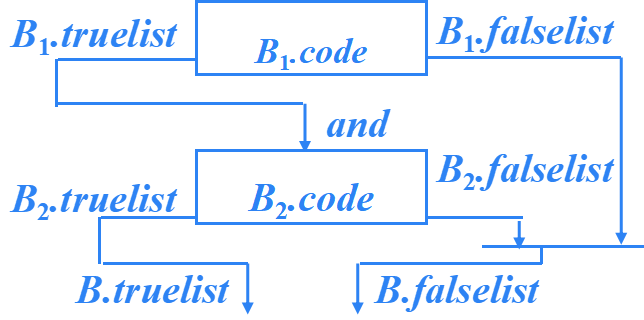
?B→ B1 and B2
B → B1 and M B2 {
??? ?backpatch( B1.truelist, M.quad ); ?
?? ?B.truelist = B2.truelist;
??? ?B.falselist = merge( B1.falselist, B2.falselist );
}
?例子
B → ?E1 relop E2 {
?? ?B.truelist = makelist(nextquad);
?? ?B.falselist = makelist(nextquad+1); ?
?? ?gen(‘if ’ E1.addr relop E2.addr ‘goto _’); ??
? ?gen(‘goto _’);
}
?100: if a<b goto _
101: goto _
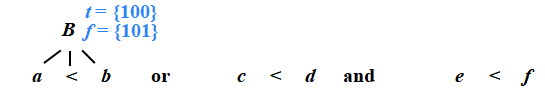
?B → B1 or M B2 {
??? ?backpatch(B1.falselist, M.quad ); ?
?? ?B.truelist= merge(B1.truelist,B2.truelist );
??? ?B.falselist = B2.falselist ;
}
M → ε {?
? ?M.quad = nextquad ;
}
100: if a<b goto _
101: goto _
102: if c<d goto _
103: goto _
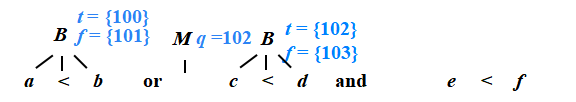
?B → B1 and M B2 {
??? ?backpatch( B1.truelist, M.quad ); ?
?? ?B.truelist = B2.truelist;
??? ?B.falselist = merge( B1.falselist, B2.falselist );
}
100: if a<b goto _
101: goto _
102: if c<d goto _
103: goto _
104: if e<f goto _
105: goto _
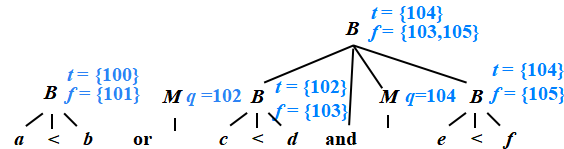
?B → B1 or M B2 {
??? ?backpatch(B1.falselist, M.quad ); ?
?? ?B.truelist= merge(B1.truelist,B2.truelist );
??? ?B.falselist = B2.falselist ;
}
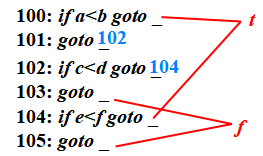
控制流語句的回填
文法:
S→ S1 S2
S →id = E ; | L = E ;?? ? ?
S →if B then S1
? ? ? | if B then S1 else S2
? ? ? | while B do S1
綜合屬性
S.next1ist:指向一個包含跳轉指令的列表,這些指令最終獲得的目標標號就是按照運行順序緊跟在S代碼之后的指令的標號
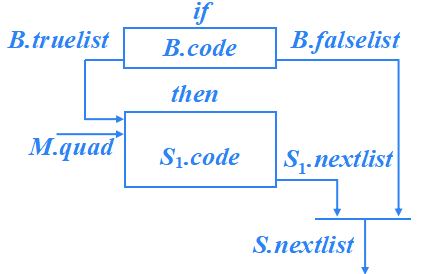
S → if B then S1
S → if B then M S1 {
??? ?backpatch(B.truelist, M.quad); ?
? ? S.nextlist=merge(B.falselist, S1.nextlist);
}
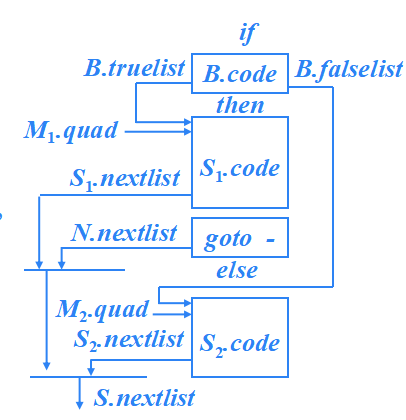
?S → if B then S1 else S2
S → if B then M1 S1 N else M2 S2 {
?? ?backpatch(B.truelist, M1.quad);
??? ?backpatch(B.falselist, M2.quad); ?
?? ?S.nextlist = merge( merge(S1.nextlist,? N.nextlist), S2.nextlist );
}
N → ε ? {
? ?N.nextlist = makelist(nextquad);
? ?gen(‘goto _’);
}
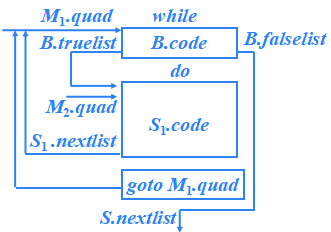
S → while B do S1
S →?while M1 B do M2 S1 {
?? ?backpatch( S1.nextlist, M1.quad );
??? backpatch( B.truelist, M2.quad );
??? S.nextlist = B.falselist;
??? ?gen(‘goto’ M1.quad);
}
?S → S1 S2
S → S1 M S2 {
?? ?backpatch( S1.nextlist, ?M.quad );
??? S.nextlist = S2.nextlist ;
}
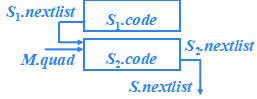
?S → id = E ; | L = E ;
S→ id = E ; | L = E ;{ S.nextlist = null; }?
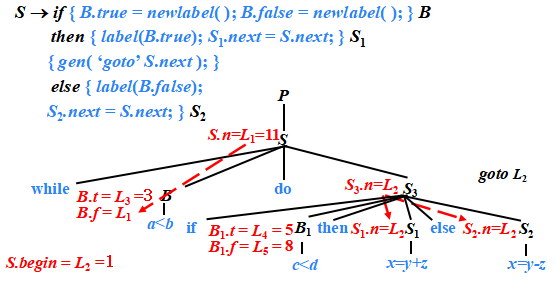
例子
while ?a < b ?do
?? ???if ?c < 5 ?then
?? ??? ? ?while x > y do z = x + 1;
? ? ? else
? ? ? ? ? ?x = y;
語句“while a<b do if c<5 then while x>y do z=x+1; else x=y;”的注釋分析樹
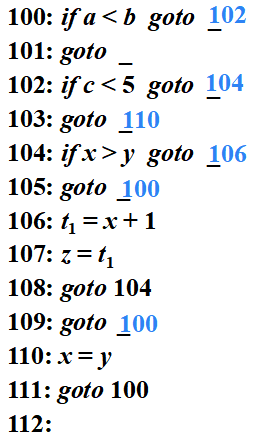
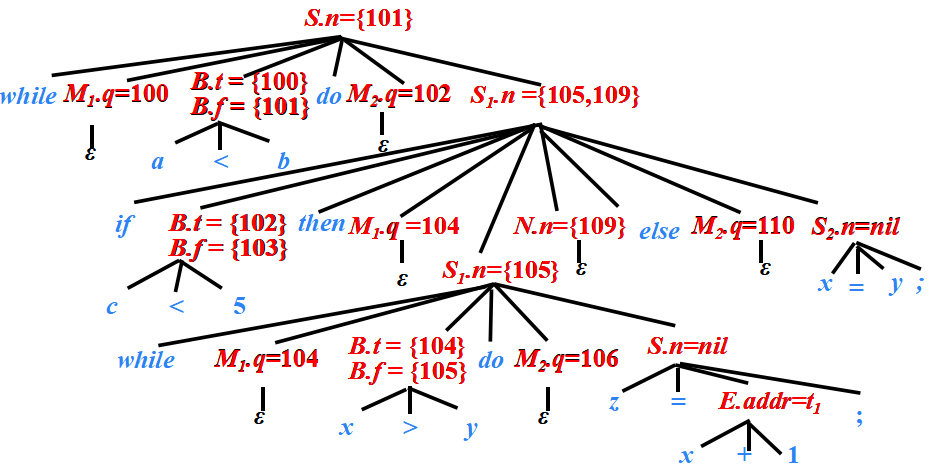
?while a<b do if c<5 then while x>y do z=x+1; else x=y;
100: if a < b ?goto 102? ? ? ? ? ? ? ? ? ? ??100:?? ?( j<, a ,b , 102 )
101: goto _? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?101: ?? ?( j ?, - , ?- , ?- ? ? )
102: if c < 5 ?goto 104? ? ? ? ? ? ? ? ? ? ? ?102: ?? ?( j<, c , 5 , 104 )
103: goto 110? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??103: ?? ?( j ?, - , ?- , 110 )
104: if x > y ?goto 106? ? ? ? ? ? ? ? ? ? ? ?104: ?? ?( j>, x , y , 106 )
105: goto 100? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 105: ?? ?( j ?, - , ?- , 100 )
106: t1 = x + 1? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?106: ?? ?( + , x , 1 , ? t1 ?)
107: z = t1? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?107: ?? ?( = , t1 , - , ? z ? )
108: goto 104? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??108: ?? ?( j ?, - , ?- , 104 )
109: goto 100? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 109: ?? ?( j ?, - , ?- , 100 )
110: x = y? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 110: ?? ?( = , y , ?- , ? x ?)
111: goto 100? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 111: ?? ?( j ?, - , ?- , 100 )
112:? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?112:
switch語句的翻譯
switch E
?? ?begin
?? ??? ?case V1: S1
?? ??? ?case V2: S2
?? ??? ?. . .
?? ??? ?case Vn – 1: Sn – 1
?? ??? ?default: Sn
?? ?end
switch E { t = newtemp(); gen( t ‘=’ E.addr ); }
case V1:{ L1= newlabel(); gen(‘if’ t ‘!=’ V1 ‘goto’ L1 ); } S1{ next = newlabel();gen(‘goto’ next); }
case V2:{ label(L1); L2=newlabel();? gen(‘if’ t ‘!= ’ V2 ‘goto’ L2 ); } S2{ gen(‘goto’ next); }
?? ??? ?. . .
case Vn -1:{ label(Ln-2); Ln-1=newlabel(); gen(‘if’ t ‘!=’ Vn-1 ‘goto’ Ln-1 );} Sn – 1{ gen(‘goto’ next);}
default:{ label(Ln-1);} Sn{label(next);}?? ?
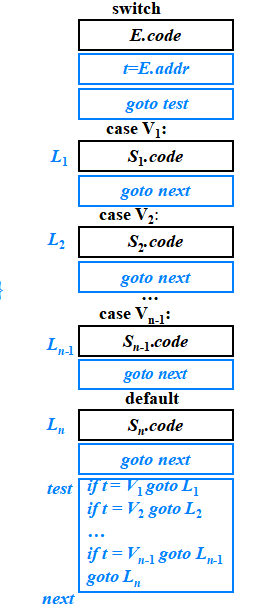
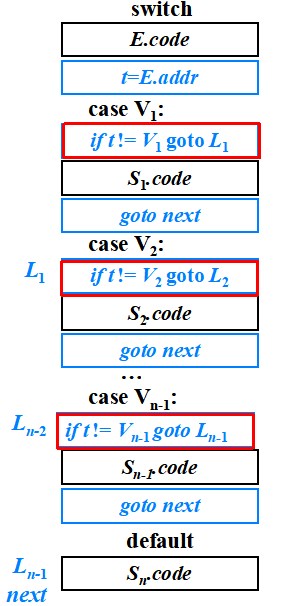
switch語句的另一種翻譯
在代碼生成階段,根據分支的個數以及這些值是否在一個較小的范圍內,這種條件跳轉指令序列可以被翻譯成最高效的n路分支
switch E { t = newtemp(); gen(t ‘=’E.addr); test = newlabel(); gen(‘goto’ test); }
case V1 : { L1= newlabel(); label(L1); map(V1, L1); }? S1 ? ?{ next = newlabel(); ?gen(‘goto’ next); }
case V2 : { L2 = newlabel(); label(L2); map(V2, L2); } ? S2 ? ?{ gen(‘goto’ next); } ?
? ??? ?. . .
case Vn-1:{ Ln-1= newlabel(); label(Ln-1); map(Vn-1, Ln-1); }? ?Sn-1 ?{ gen(‘goto’ next); }
default : ?{ Ln= newlabel(); label(Ln); }?
? ? ? ? Sn??{ gen(‘goto’ next);label(test);
? ? ? ? ? ? ? ? gen(‘if ’ t ‘=’ V1 ‘goto’ L1);
? ? ? ? ? ? ? ? gen(‘if ’ t ‘=’ V2 ‘goto’ L2);
? ? ? ? ? ? ? ? . . .
? ? ? ? ? ? ? ? gen(‘if ’ t ‘=’ Vn-1 ‘goto’ Ln-1);??
? ? ? ? ? ? ? ? gen(‘goto’ Ln);
? ? ? ? ? ? ? ?label(next);? ?}
增加一種case指令
test : ?? if t = V1 goto L1? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??test :?? ?case t ?V1 ? ? ?L1
? ? ? ? ? ?if t = V2 goto L2? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? case t ?V2 ? ?L2
? ? ? ? ? ?. . .? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?. . .
? ? ? ? ? ?if t = Vn-1 goto Ln-1? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??case t ?Vn-1 ?Ln-1
? ? ? ? ? ?goto Ln? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??case t ? t ? ? ?Ln
next :? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?next :
指令 case t Vi ?Li ?和 if t = Vi ?goto Li 的含義相同,但是case指令更加容易被最終的代碼生成器探測到,從而對這些指令進行特殊處理
過程調用語句的翻譯
文法
S → call id (Elist) ??
Elist → Elist, E ?? ?
Elist → E
過程調用語句的代碼結構
id( E1, E2, … , En )
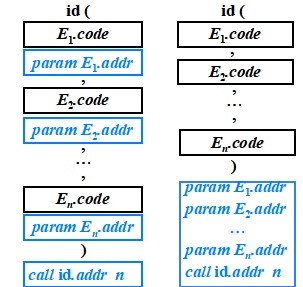
?需要一個隊列q存放E1.addr 、E2.addr、…、 En.addr,以生成
param E1.addr
param E2.addr …
param En.addr
call id.addr ?n
過程調用語句的SDD
S → call id ( Elist )
?? ?{?? ?n=0;??// 參數個數計數
?? ? ??? ?for q中的每個t ?do
?? ??? ?{?? ?gen(‘param’ t );??// 生成 param 指令
?? ??? ??? ?n = n+1;
?? ? ??? ?}
?? ??? ?gen(‘call’ id.addr ‘,’ n);???// 生成函數調用指令
?? ?}
Elist → E?
?{ ??? ?將q初始化為只包含E.addr; ?? ?}??// 一個參數時,隊列中只有一個元素
Elist →Elist1, E ?
??{ ?? ?將E.addr添加到q的隊尾; ?? ?}? ??// 多個參數就一個個拼進去
S → call id (Elist)
這就是一個函數調用,比如
call f(...),Elist是參數列表。在翻譯時我們:
先翻譯每個實參
E,把結果臨時變量加入到q(參數隊列)里;然后一條條地生成
param 參數的中間代碼;最后調用函數:
call f, 參數個數
例子
翻譯以下語句f ( b*c-1, x+y, x, y )
t1 =b*c
t2 =t1 - 1
t3 =x+y
param t2
param t3
param x
param y
call f, 4
源代碼是:f(b*c-1, x+y, x, y)
這是一個調用函數
f,傳入了 4 個實參:
b * c - 1
x + y
x
y第一個參數:
b*c - 1
t1 = b * c
t2 = t1 - 1加入隊列:
q = [t2]第二個參數:
x + y
t3 = x + y加入隊列:
q = [t2, t3]第三個參數:
x(變量)
加入隊列:
q = [t2, t3, x]第四個參數:
y(變量)
加入隊列:
q = [t2, t3, x, y]最終生成中間代碼:
t1 = b * c ? ? ? ? // 第一個參數的第一步
t2 = t1 - 1 ? ? ? ?// 第一個參數的第二步
t3 = x + y ? ? ? ? // 第二個參數
param t2 ? ? ? ? ? // 參數從左到右一個個入棧
param t3
param x
param y
call f, 4 ? ? ? ? ?// 調用 f,傳 4 個參數












)


實現方式與測試方法)

)
![[IRF/Stack]華為/新華三交換機堆疊配置](http://pic.xiahunao.cn/[IRF/Stack]華為/新華三交換機堆疊配置)


