?昨天和之前打比賽的隊友聊天，他說他面百度面到這道算法題，然后他用暴力法解的，面試官讓他優化他沒優化出來，這道題我之前沒寫過，我就想看看我能不能用效率高一點的方法把它做出來，我一開始就在想用遞歸或者翻轉字符串等等技巧，想了半個多小時都想不到，然后算了，我也用暴力法吧，然后就寫了如下代碼：

class Solution {public String longestPalindrome(String s) {int n = s.length();String ans = "";for(int i = 0;i<n;i++){int l = i, r=i;while(l<= r && l >=0 && r < n && s.charAt(l) == s.charAt(r)){String tem =s.substring(l,r+1);if(r-l+1 > ans.length())ans=tem;l--;r++;}l = i;r=l+1;while(l >=0 && r < n && s.charAt(l) == s.charAt(r)){String tem =s.substring(l,r+1);if(r-l+1 > ans.length())ans=tem;l--;r++;}}return ans;}}

這個暴力法就非常簡單了，就是遍歷字符的每個字符，然后以這個字符為中心用左右指針往兩邊移動，然后是寫了兩個while，一個是左右指針指向同一個字符然后向左右移動，還有一個是左右指針指向相鄰的字符向兩邊移動。

還是看看官方題解的做法吧。

題解的方法一是用的動態規劃：

class Solution {public String longestPalindrome(String s) {int len = s.length();if(len < 2)return s;boolean[][] dp = new boolean[len][len];for(int i=0;i<len;i++){dp[i][i] = true;}int begin =0;int maxLen =1;char[] str = s.toCharArray();for(int L =2;L<=len;L++){for(int i=0;i<len;i++){int j = i+L-1;if(j>=len){break;}else{if(str[i] != str[j]){dp[i][j] = false;}else{if(j-i<3){dp[i][j] = true;}else{dp[i][j] = dp[i+1][j-1];}}}if(dp[i][j] && j-i+1 > maxLen){maxLen = j-i+1;begin = i;}}}return s.substring(begin, begin+maxLen);}}

dp[i][j]表示s的第i個字符到第j個字符這一個子串是不是一個回文字符串。

首先，初始狀態：dp[i][i] = true；

然后，狀態轉移方程：dp[i][j] = ?

第一種情況，s.charAt(i) != s.charAt(j), 那么dp[i][j] = false;

第二種情況，s.charAt(i) == s.charAt(j)，如果子串長度小于3，那么dp[i][j]=true;否則dp[i][j] = dp[i-1][j+1]

只要找出dp[i][j]中為true且長度最大的那個就行，這一步在填充dp的數組的同時進行，不用另外遍歷，只要一個max動態更新就行。然后值得注意的是這里是把字符串轉成了字符數組，因為我們需要頻繁的找字符串中的字符，用數組效率更高，用charAt方法需要遍歷字符串，而數組可以直接通過尋址公式得出。

題解的第二種方法用的是中心擴展，和我的方法差不多，只是它把while循環封裝成了函數而已，以下是題解方法二代碼：

class Solution {public String longestPalindrome(String s) {if (s == null || s.length() < 1) {return "";}int start = 0, end = 0;for (int i = 0; i < s.length(); i++) {int len1 = expandAroundCenter(s, i, i);int len2 = expandAroundCenter(s, i, i + 1);int len = Math.max(len1, len2);if (len > end - start) {start = i - (len - 1) / 2;end = i + len / 2;}}return s.substring(start, end + 1);}public int expandAroundCenter(String s, int left, int right) {while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {--left;++right;}return right - left - 1;}
}

題解的方法三就比較高級了，時間復雜度只有O(n)，叫Manacher算法：

定義一個概念”臂長“，如果一個回文字符串的長度是2*lenght+1,那么這個回文字符串的臂長就是length。

如果位置j的臂長為length那么如何找到位置i的臂長呢？

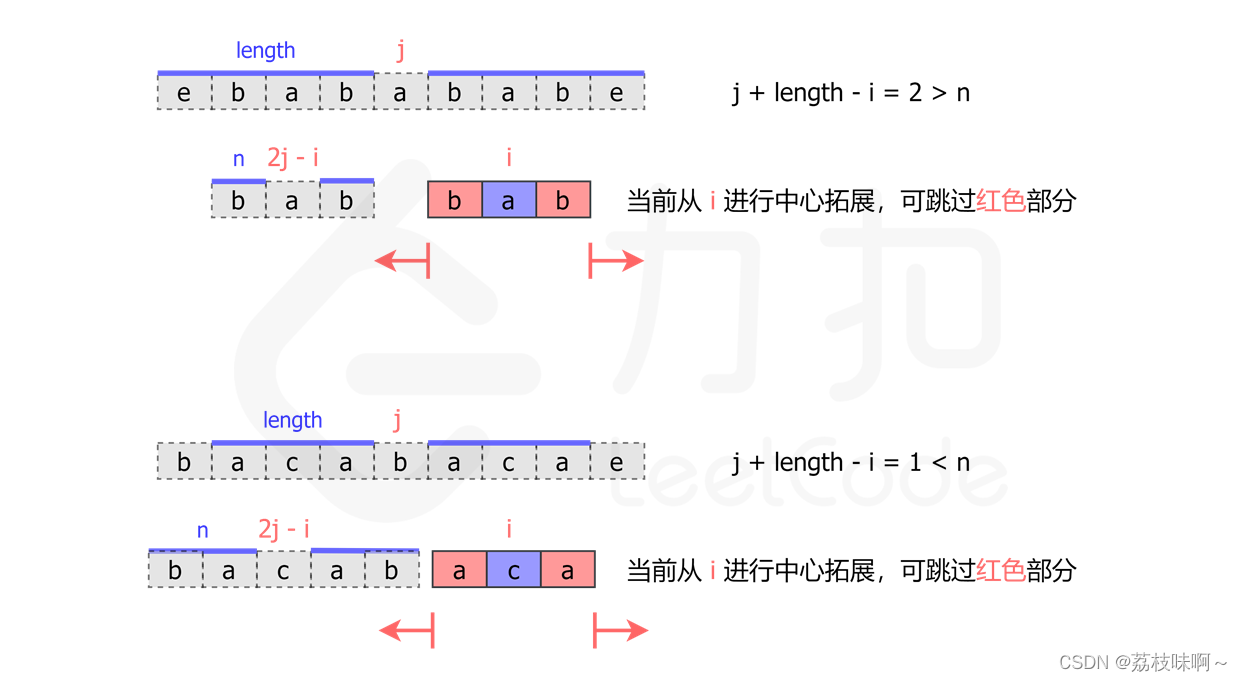
對于奇數長度的回文字符串而言：

如果i關于j的對稱點2*j-i的臂長是n，那么位置i的臂長是min(n,2*j-i)。這個其實很好理解，因為j左右length拿一段是對稱的，所以如果2*j-i有n的臂長按道理i也是這么大的臂長，但是只有length這一部分是對稱的，而2*j-i的對稱部分還可以向兩邊擴展，所以i的臂長只能取n和2*j-i的最小值。

偶數長度的回文字符串呢？

我們通過在字符串的兩頭和沒兩個字符之間加上#，這樣無論奇數還是偶數長度的回文字符串都變成了奇數長度的回文字符串，比如aaba處理成#a#a#b#a#，偶數長度的回文字符串aa變成了#a#a#。aba還是變成奇數#a#b#a#。需要注意的是這里添加的#需要是字符串里面沒有出現過的。最后記得把回文字符還原，把#去掉。以下是Manacher方法的代碼：

class Solution {public String longestPalindrome(String s) {int start = 0, end = -1;StringBuffer t = new StringBuffer("#");for (int i = 0; i < s.length(); ++i) {t.append(s.charAt(i));t.append('#');}t.append('#');s = t.toString();List<Integer> arm_len = new ArrayList<Integer>();int right = -1, j = -1;for (int i = 0; i < s.length(); ++i) {int cur_arm_len;if (right >= i) {int i_sym = j * 2 - i;int min_arm_len = Math.min(arm_len.get(i_sym), right - i);cur_arm_len = expand(s, i - min_arm_len, i + min_arm_len);} else {cur_arm_len = expand(s, i, i);}arm_len.add(cur_arm_len);if (i + cur_arm_len > right) {j = i;right = i + cur_arm_len;}if (cur_arm_len * 2 + 1 > end - start) {start = i - cur_arm_len;end = i + cur_arm_len;}}StringBuffer ans = new StringBuffer();for (int i = start; i <= end; ++i) {if (s.charAt(i) != '#') {ans.append(s.charAt(i));}}return ans.toString();}public int expand(String s, int left, int right) {while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {--left;++right;}return (right - left - 2) / 2;}
}