目錄

一、課題描述

輸入樣例：

輸出樣例：

二、需求分析

輸入的形式和輸入值的范圍：

輸出的形式：

程序所能達到的功能：

三、概要設計

四、流程圖

五?、代碼+詳細注釋

六、測試數據和結果

---

一、課題描述

以一個 m*n 的方陣表示迷宮，0 和 1 分別表示迷宮中的通路和障礙。設計一個程序，對任意設定的迷宮，求出一條從入口到出口的最短通路，或得出沒有通路的結論。

輸入樣例：

5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0

輸出樣例：

8

二、需求分析

本設計程序用C++ 編寫，完成二維數組迷宮的生成，找到走出迷宮的最短路徑，或者返回沒有通路的結論。

• 輸入的形式和輸入值的范圍：

• 輸入格式:第一行包含兩個整數 n 和 m。接下來 n行，每行包含 m 個整數（0 或 1），表示完整的二維數組迷宮。數據范圍：1≤n,m≤100。

• 輸出的形式：

• 輸出一個整數，表示從左上角移動至右下角的最少移動次數。

???程序所能達到的功能：

? ? 1.找到一條從入口到出口的最短通路2.如果迷宮內沒有通路，則返回沒有通路的結論。

三、概要設計

1 ）數據邏輯結構、存儲結構分析：

（1 ） 數據邏輯結構：

在迷宮求解的問題中，我運用了隊列這種線性結構來存儲最新到達的地點，隊頭出隊即表示該點走向下一個結點。

（2 ）存貯結構分析：

在迷宮求解的問題中，我運用了隊列這種順序結構，隊列在這個代碼中的作用是實現廣度優先搜索算法（BFS）。BFS是一種圖遍歷算法，用于在圖或二維網格中尋找最短路徑或解決某些問題。

2 ）本程序包含2 個函數：

（1 ）廣度優先搜索算法函數bfs()

1. 參數描述：

g[N][N]:存貯迷宮信息

d[N][N]:存貯各個點到起始點的路徑長度

PII q[N*N],hh,tt:模擬隊列，PII q[N*N]:存貯隊列中的數據，hh:隊頭，tt:隊尾

Dx:代表這個點在x軸的偏移量，dy:代表這個點在y軸的偏移量

1. 功能描述

初始化隊列：將起始點排入隊列中，即{0，0}。

初始化d數組：將d數組初始化為-1，從而在bfs搜索時能判斷出這個點是否被搜索過

初始化dx數組和dy數組：即存貯x和y上下左右移動時的偏移量

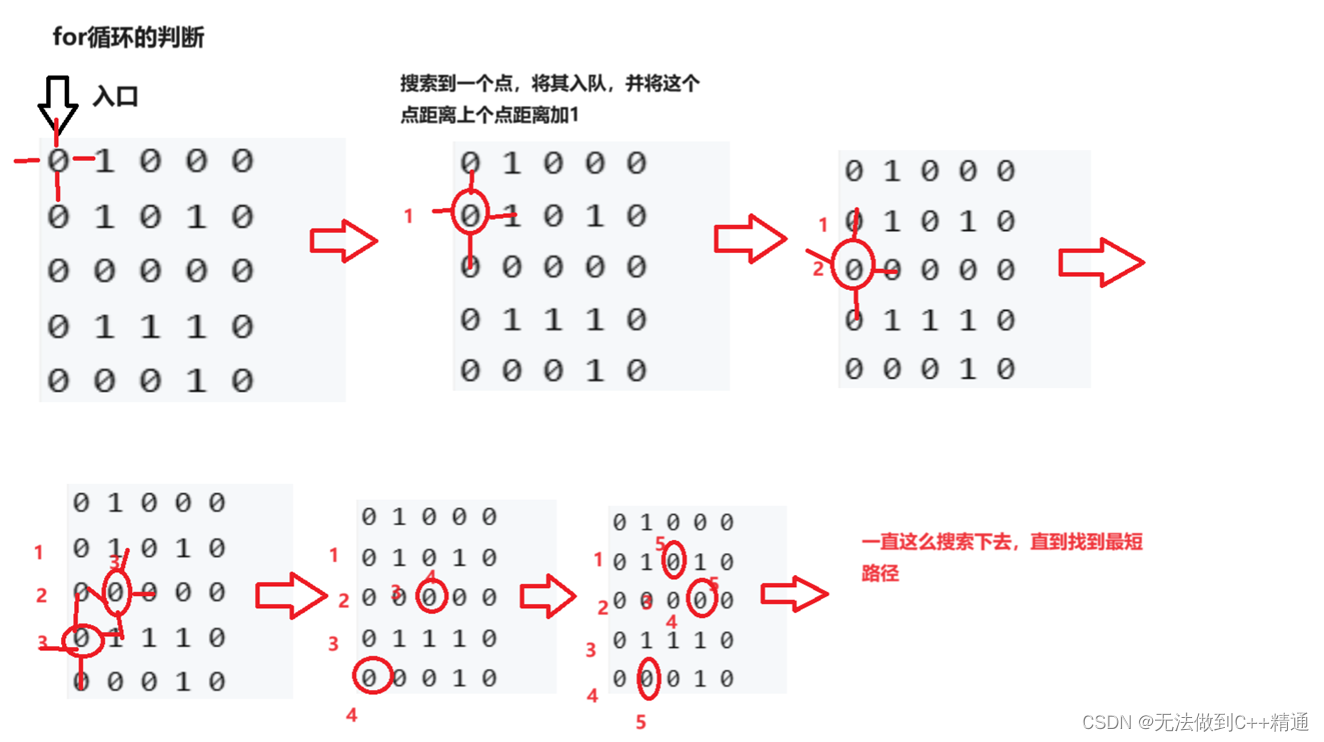
For循環判斷：將這個點進行上下左右四次移動，如果它在我的二維數組迷宮里面（未超出范圍）并且移動之后點的值等于0（能夠通行）而且是第一次通過（最短路），我就將它入隊，并且記錄它距離下一個點的距離加1，然后就是一個循環過程，只要我的隊里有元素，就說明還未找到最短路。

（2 ）主函數main()

1. 參數描述

M,n:代表m行n列的迷宮

Flag:判斷迷宮中是否有通路

1. 功能描述

初始化迷宮：輸入m行n列的迷宮

判斷返回值：將bfs得到的結果進行判斷，如果我的迷宮出口距離起始點不是-1的話（已經被搜索到過），那我就返回最短路徑，否則返回沒有通路。

四、流程圖

五?、代碼+詳細注釋

#include <iostream>
#include <algorithm>
#include <cstdio>using namespace std;typedef pair<int, int>PII;const int N = 110;
//定義一些全局變量
//n,m n行m列
//g數組 存貯迷宮
//d數組 存貯點到起始點的距離
//q二元組 存貯隊列元素點的數據
int n, m;
int g[N][N];
int d[N][N];
PII q[N * N];//重點！bfs的實現
int bfs()
{//隊頭hh,隊尾ttint hh = 0, tt = 0;//隊頭起始點{0，0}q[0] = { 0,0 };//memset函數，將d數組初始化為-1，主要是用于后面判斷此點是否被用過memset(d, -1, sizeof d);//將起始點距離初始化為0d[0][0] = 0;//用數組dx和dy分別存貯x和y和偏移量int dx[4] = { -1,0,1,0 }, dy[4] = { 0,1,0,-1 };//只要我的隊列中有元素，就說明廣度搜索沒搜索完while (hh <= tt){//將隊頭元素彈出賦值給t//auto t其實就等于pair<int,int> t(auto 就是讓系統自己猜出t的變量類型，不需要我寫出冗雜的代碼)auto t = q[hh++];//將隊頭彈出的點進行上下左右四次偏移for (int i = 0; i < 4; i++){//t.first即指pair這個二元組前一個元素，t.second即后一個元素//這一步就是得到移動后x，y的坐標int x = t.first + dx[i], y = t.second + dy[i];//判斷移動后的點是否能入隊//x >= 0 && x < n && y >= 0 && y < m首先這個點不能超出我的迷宮邊界//g[x][y] == 0 其次這個點得是我能通行的（即在這個迷宮上這個點的值為0）//d[x][y] == -1 由于我上面有過的初始化，所以d[x][y] == -1時代表這個點第一次被搜索//下一次搜索到這個點我就不要了，就不是最短路徑了if (x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1){//用d數組記錄點到起始點的距離d[x][y] = d[t.first][t.second] + 1;//最后將bfs搜索到的點入隊，進行下一次搜索q[++tt] = { x,y };}}}//最后返回終點距離起始點的距離return d[n - 1][m - 1];
}int main()
{cin >> n >> m;//輸入我的迷宮for (int i = 0; i < n; i++)for (int j = 0; j < m; j++)cin >> g[i][j];//用flag接收bfs函數返回的值int flag = bfs();//如果返回的值等于-1的話，說明我的bfs并沒有搜索到最后的出口，即這條迷宮沒有通路//反之則有通路，并且是最短通路if (flag!=-1) cout << flag << endl;else cout << "此迷宮中，沒有道路能走出去" << endl;return 0;
}

六、測試數據和結果

測試數據1

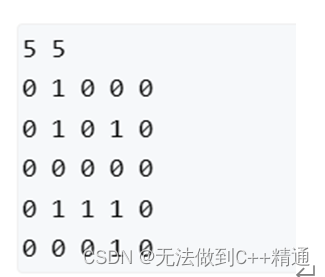
測試結果：

測試數據2：

測試結果：

測試數據3：

測試數據4：

測試結果：