Matlab數學建模算法之小波神經網絡詳解

🔗?運行環境：Matlab

🚩?撰寫作者：左手の明天

🥇?精選專欄：《python》

🔥??推薦專欄：《算法研究》

🔐####?防偽水印——左手の明天?####🔐

💗 大家好🤗🤗🤗，我是左手の明天！好久不見💗

💗今天分享matlab數學建模算法——小波分析💗

📆? 最近更新：2023 年 12 月 05 日，左手の明天的第?302?篇原創博客

📚?更新于專欄：matlab

🔐####?防偽水印——左手の明天?####🔐

一、小波神經網絡

小波神經網絡（Wavelet Neural Network，簡稱WNN）是基于小波變換理論構造而成，其原理與反向傳播神經網絡（BPNN）較為接近。最主要的特征是它的隱含層神經元激活函數為小波基函數，這一特性使其充分利用了小波變換的局部化性質和神經網絡的大規模數據并行處理、自學習能力，因而具有較強的逼近能力和較快的收斂速度。

小波神經網絡的結構圖如下圖所示：

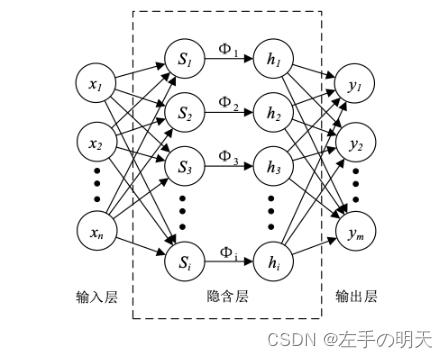
二、小波分析

小波分析是一種強大的數學工具，它在信號處理、圖像處理、量子力學等領域有著廣泛的應用。小波變換是一種將信號分解成不同尺度的成分，以便更好地理解信號的特性的方法。

1、小波變換的定義

小波變換是一種信號分析方法，它可以將信號分解成不同尺度的成分。小波變換的基本思想是將信號投影到一組小波函數上，這組小波函數構成了小波基。小波基的特性是它們在時間和頻率上都具有良好的局部性。這意味著小波基可以很好地捕捉信號中的局部特征，無論在高頻還是低頻部分。

小波變換的定義基于傅里葉變換和伸縮平移運算。它通過將信號與一組小波函數進行內積運算，得到信號在不同尺度下的投影。這些投影可以理解為信號在不同尺度下的細節和概貌。

2、小波變換的性質

小波變換具有一些重要的性質，包括：

(1) 適應性和多分辨率特性：小波變換可以適應不同尺度的信號，并能夠同時處理高頻和低頻部分。這使得小波變換具有多分辨率特性，可以更好地分析信號的細節和概貌。

(2) 方向性和時間-頻率局部性：小波基具有方向性和時間-頻率局部性，這使得小波變換在處理信號時具有很好的局部性。它可以捕捉信號中的突變和邊緣等局部特征，并提供關于這些特征的更多信息。

(3) 冗余性和壓縮性：小波變換具有冗余性，這意味著它可以將信號分解成多個層次，每個層次都包含了信號的不同方面的信息。這種冗余性使得小波變換具有很好的壓縮性，可以將信號壓縮成更小的數據量。

3、小波變換的實現

小波變換的實現通常分為兩步：首先是選擇合適的小波基，然后是對信號進行小波分解和重構。選擇合適的小波基需要考慮信號的特性和應用場景。常用的有小波基包括Daubechies小波基、Haar小波基、Morlet小波基等。

小波分解是將信號分解成多個層次的過程，每個層次都包含了信號的不同方面的信息。常用的有小波分解算法包括二進小波分解、多尺度小波分解等。重構是小波變換的逆過程，它可以根據小波分解的結果將信號恢復成原始形式。

4、小波變換的數學模型

小波變換的數學模型可以通過連續小波變換和離散小波變換表示。連續小波變換是對連續信號進行小波變換，可以用積分來表示。離散小波變換是對離散信號進行小波變換，可以用矩陣運算表示。

4.1 連續小波變換

連續小波變換的數學模型可以表示為：

W(a, b) = ∫f(t)ψ*[ (t-b)/a ] dt

其中，W(a, b)表示小波系數，f(t)表示原始信號，ψ(t)表示小波基函數，a和b分別表示尺度參數和平移參數。

4.2 離散小波變換

離散小波變換的數學模型可以表示為：

W(n, k) = ∑f(m)ψ*[ (m-k)/2^n ]?

其中，W(n, k)表示小波系數，f(m)表示原始信號，ψ(m)表示離散小波基函數，n表示尺度參數，k表示平移參數。

5、matlab實現小波變換

在MATLAB中進行小波分析的步驟如下：

準備數據：將待分析的信號數據準備好，可以是一個向量或一個矩陣。
選擇小波類型：根據需要選擇合適的小波類型，例如Daubechies小波、Haar小波、Morlet小波等。
進行小波分解：使用MATLAB中的小波分析函數，例如dwt()或wavedec2()，對信號數據進行小波分解。這將會將信號分解成多個層次，每個層次都包含了信號的不同方面的信息。
分析小波系數：對分解后得到的小波系數進行分析，例如可以觀察近似系數和細節系數的變化情況，從而得到信號在不同層次上的特征。
重構信號：如果需要，可以使用idwt()或waverec2()函數對信號進行重構，得到原始信號。
計算相關統計量和特征量：根據需要，可以計算相關統計量和特征量，例如均方差、峰值等，以進一步分析信號的特征。

需要注意的是，在進行小波分析前，需要了解小波分析的基本原理和性質，以便更好地選擇合適的小波類型和分解方式，以及正確地解釋分析結果。

在MATLAB中進行小波分析，我們首先需要了解幾個關鍵函數：

dwt(): 這是進行一維小波單層分解的函數，它采用小波名稱作為參數，返回近似系數和細節系數。
wavdec(): 這是進行一維小波多層分解的函數，它可以將信號分解成多個層次。
idwt(): 這是進行小波重構的函數，它采用近似系數和細節系數作為參數，返回重構后的信號。

下面是一個簡單的例子，說明如何在MATLAB中使用小波分析：

% 創建信號
x = randn(1,100);
% 選擇小波類型
wname = 'db1';
% 進行一維小波分解
[cA,cD] = dwt(x,wname);
% 進行小波重構
X = idwt(cA,cD,wname);

在這個例子中，首先創建了一個隨機信號x。然后，選擇了Daubechies小波（'db1'）進行小波分解。分解后，我們得到了近似系數cA和細節系數cD。最后，我們使用idwt()函數進行了小波重構，得到了重構后的信號X。

注意：在進行小波重構時，必須使用與分解時相同的小波類型。

二維小波分析在圖像處理中特別有用。在MATLAB中，你可以使用wavedec2()函數進行二維小波分解，使用waverec2()函數進行二維小波重構。二維小波分解和重構通常用于圖像壓縮、去噪等方面。

三、權值訓練

小波神經網絡（Wavelet Neural Network，簡稱WNN）是一種結合了小波變換和神經網絡的復合體。它的權值訓練一般通過以下步驟進行：

網絡初始化：首先，對小波神經網絡進行初始化，包括確定網絡的結構、小波基函數的類型和參數、權值和閾值等。
輸入數據學習：將已知的輸入數據通過小波變換進行分解和重構，通過調整權值和閾值使得網絡的輸出盡可能接近目標輸出。
誤差反向傳播：在每個訓練周期結束后，計算網絡輸出和目標輸出的誤差，并將誤差反向傳播到網絡中，根據誤差調整權值和閾值。
權值更新：根據反向傳播的誤差，對網絡的權值進行更新。一般采用梯度下降法或其他優化算法來更新權值。
重復學習：重復步驟2-4，直到網絡的輸出與目標輸出之間的誤差滿足要求，或者達到預設的學習次數。

小波神經網絡的權值訓練過程與反向傳播神經網絡類似，都是通過不斷調整權值和閾值來最小化網絡輸出與目標輸出之間的誤差。但是，小波神經網絡的小波基函數具有更好的局部化性質和時頻分析能力，因此可以更好地處理具有復雜特征的數據。

四、特征分析

小波神經網絡利用小波基函數的性質進行特征分析主要表現在以下幾個方面：

多尺度分析：小波神經網絡可以通過多尺度分析，在不同尺度下提取信號的特征。小波基函數可以將信號分解成多個尺度的成分，每個尺度下的成分都包含了信號的不同頻率信息和細節信息。
局部化分析：小波基函數具有局部化性質，可以捕捉信號的局部特征。通過小波神經網絡對信號進行分解和重構，可以更好地提取信號中的局部特征，對于信號分類、識別等任務有很大的幫助。
方向選擇性：小波基函數在時頻域上具有方向選擇性，可以更好地適應信號的變化。通過小波神經網絡對信號進行分解和重構，可以更好地適應信號的變化，提高信號處理的準確性和魯棒性。
非線性映射：小波基函數具有非線性映射的能力，可以將輸入信號映射到高維空間中。通過小波神經網絡對輸入信號進行學習和映射，可以更好地表示輸入信號的特征，提高分類和識別的準確性。

總之，小波神經網絡利用小波基函數的性質進行特征分析，可以更好地提取信號的特征，提高信號處理的準確性和魯棒性。

五、小波基函數

小波基函數是小波分析的核心組成部分，選擇合適的小波基函數對于信號處理、圖像處理、數值分析等領域的應用非常重要。在選擇小波基函數時，需要考慮以下幾個因素：

5.1 支撐長度（Support Length）

小波基函數的支撐長度是指在一定尺度下，小波基函數的非零部分所覆蓋的信號長度。一般來說，支撐長度越長，小波基函數就越能捕捉到信號中的細節和特征，但同時也會增加計算的復雜性和內存消耗。因此，在選擇小波基函數時，需要根據應用場景和硬件資源進行權衡。

常見的支撐長度有小波基函數的名稱和對應的支撐長度（在MATLAB環境下）：

Daubechies 2 (db2): 3
Daubechies 3 (db3): 4
Daubechies 4 (db4): 5
Daubechies 5 (db5): 6
Daubechies 6 (db6): 7
Daubechies 8 (db8): 9
Daubechies 12 (db12): 13
Daubechies 14 (db14): 15

5.2 緊支撐（Tight Support）

緊支撐是指小波基函數在時間和頻率域中的局部化性質，即在小波變換的過程中，只有靠近輸入信號的位置才會產生非零系數。選擇具有緊支撐的小波基函數可以減少計算量和內存消耗，同時提高信號處理的效率和準確性。

在選擇小波基函數時，需要考慮其緊支撐性質。一般來說，Daubechies系列小波基函數具有較好的緊支撐性質。此外，還可以根據應用場景和問題特點來選擇具有合適支撐長度和緊支撐的小波基函數。例如，當處理信號的頻率成分較為復雜時，可以選擇支撐長度較長的小波基函數；當處理信號的時域特征較為重要時，可以選擇具有較好緊支撐性質的小波基函數。

總之，選擇合適的小波基函數需要考慮支撐長度和緊支撐等因素，同時結合具體的應用場景和問題特點進行選擇。在MATLAB環境下，可以使用wfilters函數來查看不同小波基函數的性質和特點，以便選擇合適的小波基函數進行應用。

六、小波神經網絡實現過程

步驟1：數據準備

首先，我們需要準備用于訓練和測試的數據集。數據集應包含輸入樣本和對應的目標輸出。確保數據集經過預處理和歸一化處理，便于網絡的訓練和學習。

步驟2：網絡建立

使用MATLAB的神經網絡工具箱，我們可以方便地建立小波神經網絡。首先，定義網絡的拓撲結構和參數配置，包括輸入層、隱藏層和輸出層的節點數，以及學習率、最大迭代次數等參數。

步驟3：訓練網絡

使用訓練數據集對小波神經網絡進行訓練。在MATLAB中，可以使用train函數來訓練神經網絡。通過設置訓練選項，可以控制訓練過程的細節和收斂性。

步驟4：測試網絡

使用測試數據集對訓練好的小波神經網絡進行測試，以評估其性能和泛化能力。在MATLAB中，可以使用sim函數來模擬網絡的響應。通過比較網絡的輸出和目標輸出，可以計算誤差和評估網絡的性能。

步驟5：應用網絡

使用訓練好的小波神經網絡對新的輸入數據進行威脅評估。將新的輸入數據輸入到網絡的輸入層，通過隱藏層和輸出層的計算，得到威脅評估結果。

以上是一個簡單的小波神經網絡實現過程。在實際應用中，可能需要根據具體情況進行適當的調整和優化。同時，也可以考慮使用其他工具或框架來實現小波神經網絡，如MATLAB的Deep Learning Toolbox、Python的PyWavelets和Scikit-Learn等。

七、MATLAB實現的小波神經網絡

以下是一個使用MATLAB實現的小波神經網絡代碼示例：

% 加載數據集
load iris_dataset% 定義小波神經網絡結構
net = newff(input, target, [10 1], {'logsig', 'purelin'}, 'trainlm');% 設置訓練參數
net.trainParam.epochs = 100;
net.trainParam.goal = 1e-5;
net.trainParam.show = 10;
net.trainParam.lr = 0.01;
net.trainParam.mc = 0.9;% 訓練網絡
[net, tr] = train(net, input, target);% 測試網絡性能
output = net(input);
perf = perform(net, target, output);

在上述代碼中，首先加載了鳶尾花數據集，并定義了一個具有10個隱層節點和1個輸出節點的小波神經網絡。使用了logsig激活函數作為隱層激活函數，并使用purelin激活函數作為輸出層激活函數。然后，設置了網絡的訓練參數，包括最大迭代次數、目標誤差、顯示間隔、學習率和動量等。最后，使用train函數訓練了網絡，并使用perform函數評估了網絡的性能。

function main()
clc;clear all;close all;
%用Mexihat函數作為樣本輸入和輸出
x=0:0.03:3; %樣本輸入值
c=2/(sqrt(3).*pi.^(1/4));
d=1/sqrt(2);
u=x/2-1;
targ=d.*c.*exp(-u.^2/2).*(1-u.^2);  % 目標函數的樣本輸出值
eta=0.02;aerfa=0.735; %賦予網絡學習速率和動量因子初始值
%初始化輸出層和隱層的連接權wjh和隱層和輸出層的連接權.
%假設小波函數節點數為H,樣本數為P,輸出節點數為J,輸入節點數為I.
H=15;P=2;I=length(x);J=length(targ);
b=rand(H,1);a=rand(H,1); %初始化小波參數
whi=rand(I,H);wjh=rand(H,J); %初始化權系數；
b1=rand(H,1);b2=rand(J,1);%閾值初始化;
p=0;
Err_NetOut=[];%保存的誤差；
flag=1;count=0;
while flag>0
flag=0;
count=count+1;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
xhp1=0;
for h=1:Hfor i=1:Ixhp1=xhp1+whi(i,h)*x(i);end
ixhp(h)=xhp1+b1(h);
xhp1=0;
end
for h=1:H
oxhp(h)=fai((ixhp(h)-b(h))/a(h));
end
ixjp1=0;
for j=1:Jfor h=1:Hixjp1=ixjp1+wjh(h,j)*oxhp(h);end
ixjp(j)=ixjp1+b2(j);
ixjp1=0;
end
for i=1:J
oxjp(i)=fnn(ixjp(i));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
wuchayy=1/2*sumsqr(oxjp-targ);
Err_NetOut=[Err_NetOut wuchayy];%保存每次的誤差;
%求解小波網絡運用BP算法，各參數每次學習的調整量
for j=1:J
detaj(j)=-(oxjp(j)-targ(j))*oxjp(j)*(1-oxjp(j));
end
for j=1:Jfor h=1:Hdetawjh(h,j)=eta*detaj(j)*oxhp(h);end
end
detab2=eta*detaj;
sum=0;
for h=1:Hfor j=1:Jsum=detaj(j)*wjh(h,j)*diffai((ixhp(h)-b(h))/a(h))/a(h)+sum;end
detah(h)=sum;
sum=0;
end
for h=1:Hfor i=1:Idetawhi(i,h)=eta*detah(h)*x(i);end
end
detab1=eta*detah;
detab=-eta*detah;
for h=1:H
detaa(h)=-eta*detah(h)*((ixhp(h)-b(h))/a(h));
end
%引入動量因子aerfa，加快收斂速度和阻礙陷入局部極小值.
wjh=wjh+(1+aerfa)*detawjh;
whi=whi+(1+aerfa)*detawhi;
a=a+(1+aerfa)*detaa';
b=b+(1+aerfa)*detab';
b1=b1+(1+aerfa)*detab1';
b2=b2+(1+aerfa)*detab2';
%本算法采用的是樣本逐個處理而不是數據批處理
p=p+1;
if p~=P
flag=flag+1;
else
if Err_NetOut(end)>0.008
flag=flag+1;
else
figure;
plot(Err_NetOut);
xlabel('網絡學習的次數');ylabel('網絡輸出的誤差');
title('網絡學習誤差曲線','fontsize',20,'color',[0 1 1],'fontname','隸書');
end
end
if count>6000
figure(1);
subplot(1,2,1)
plot(Err_NetOut,'color','b','linestyle','-','linewidth',2.2,...
'marker','^','markersize',3.5);
xlabel('網絡學習的次數');ylabel('網絡輸出的誤差');
title('誤差曲線','fontsize',20,'color',[1 1 1],'fontname','隸書');
subplot(1,2,2)
handle1=plot(x,targ,'color','r','linestyle','--','linewidth',2.2,...
'marker','p','markersize',3.5);
hold on
handle1=plot(x,oxjp,'color','g','linestyle','-.','linewidth',2.2,...'marker','d','markersize',3.5);
xlabel('樣本輸入值');ylabel('樣本目標值與網絡輸出值');
title('目標值與網絡輸出值比較','fontsize',20,'color',[1 1 1],'fontname','隸書');
legend('樣本目標值','網絡仿真值');
break;
end
end
function y3=diffai(x)  %子程序
y3=-1.75*sin(1.75*x).*exp(-x.^2/2)-cos(1.75*x).*exp(-x.^2/2).*x;
function yl=fai(x)  %子程序
yl=cos(1.75.*x).*exp(-x.^2/2);
function y2=fnn(x)  %子程序
y2=1/(1+exp(-x));