一? ?什么是回溯算法
回溯算法(Backtracking Algorithm)是一種用于解決組合優化問題的算法,它通過逐步構建候選解并進行驗證,以尋找所有滿足特定條件的解。回溯算法通常應用于在給定約束條件下枚舉所有可能解的問題,如組合、排列、子集等。
回溯算法的基本思想是通過遞歸的方式進行搜索,每一步都嘗試擴展當前的解,直到找到滿足條件的解或者確定無解。在搜索的過程中,如果當前的解不滿足約束條件,就會回溯到上一步進行其他選擇,繼續搜索。
回溯算法的一般步驟如下:
- 定義問題的解空間,確定問題的約束條件。
- 通過遞歸的方式搜索解空間,每一步都進行選擇,并進行約束條件的檢查。
- 如果當前的選擇滿足約束條件,則繼續遞歸地進行下一步選擇。
- 如果當前的選擇不滿足約束條件,進行回溯,撤銷當前選擇,返回上一步繼續搜索其他選擇。
- 當搜索完成后,得到所有滿足條件的解。
回溯算法的時間復雜度通常較高,因為它需要枚舉所有可能的解。在某些情況下,可以通過剪枝等優化策略來減少搜索空間,提高算法效率。
回溯算法在很多問題中都有應用,例如八皇后問題、0-1背包問題、圖的遍歷等。它是一種非常經典和常用的算法思想,對于解決組合優化問題具有重要的作用。
通常解該類題目時,我們要確定解的空間,從而很好的利用回溯算法來解決該類題目。
二? ?何為解空間
? ? ? 解空間(Solution Space)是指在給定問題的約束條件下,所有可能的解的集合。它包含了問題的所有合法解。
? ? ? 解空間的具體形式取決于問題的性質和約束條件。對于某些問題,解空間可能是一個有限的集合,例如在數獨游戲中,解空間是由符合數獨規則的所有數字填充方案組成的集合。而對于其他問題,解空間可能是一個無限的集合,例如在連續優化問題中,解空間是由實數構成的無限維空間。
? ? ?解空間是問題求解的關鍵概念之一。在解決問題時,我們通常需要在解空間中搜索滿足特定條件的解。回溯算法、枚舉法、剪枝算法等求解方法都是基于對解空間的搜索。
? ? ? 解空間的大小直接影響了問題的復雜性和求解算法的效率。如果解空間非常大,問題的求解可能會非常困難,需要耗費更多的時間和資源。因此,在實際應用中,優化算法常常通過剪枝、啟發式搜索等技術來減小解空間的規模,以提高求解效率。
總之,解空間是問題求解中描述所有可能解的概念,通過搜索解空間,我們可以找到滿足問題要求的解或者找到最優解。
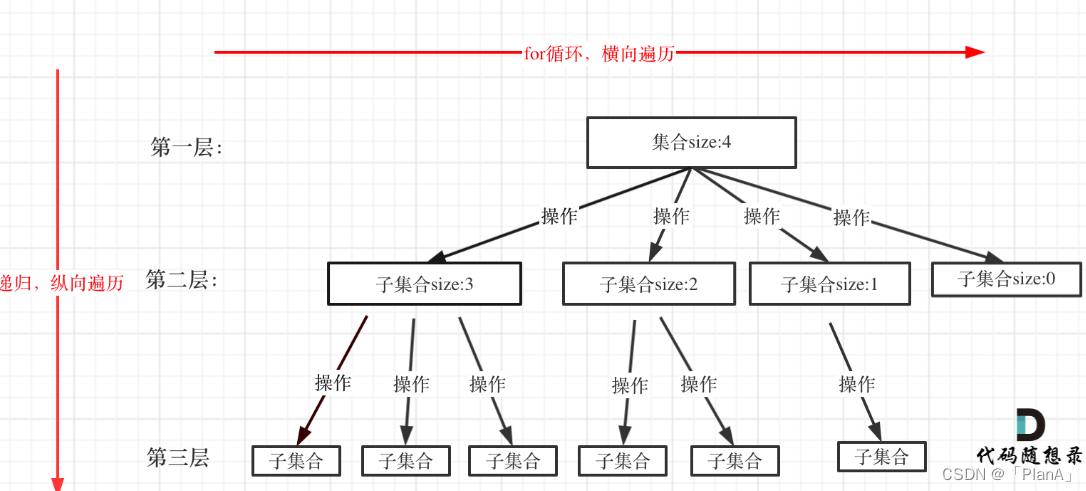
對于大多數該類問題的解空間都是樹的形式,集合的大小構成了樹的寬度,遞歸的深度構成的樹的深度。
三? ?回溯算法的模板
下面是回溯算法的一般模板:
void backtracking(參數) {if (終止條件) {存放結果;return;}for (選擇:本層集合中元素(樹中節點孩子的數量就是集合的大小)) {//橫向遍歷處理節點;//這里一般可能進行剪枝操作backtracking(路徑,選擇列表); // 遞歸,縱向遍歷回溯,撤銷處理結果}
}這是一個基本的回溯算法模板,其中的關鍵點包括:
-
定義終止條件:當滿足終止條件時,表示找到了一個解或者不再需要繼續搜索,可以進行相應的操作,如輸出結果或返回。
-
遍歷選擇列表:遍歷所有可能的選擇,通常使用循環結構,對于每個選擇,進行相應的操作。
-
做出選擇:根據當前選擇,更新狀態或路徑,表示對問題的一次選擇。
-
遞歸進入下一層決策樹:根據當前選擇,進入下一層決策樹,即進行下一步的選擇。
-
撤銷選擇:在回溯到上一層之前,需要撤銷當前選擇,恢復狀態或路徑,以便進行下一個選擇。
在實際應用中,根據具體問題的不同,模板中的代碼需要進行相應的修改和擴展,以適應問題的特點和約束條件。同時,通過剪枝、優化等技巧,可以對模板進行改進,提高算法的效率。
需要注意的是,回溯算法是一種暴力搜索的方法,解空間的規模很大時,可能會導致算法效率低下。因此,在使用回溯算法時,需要根據問題的規模和特點進行合理的優化和剪枝,以提高算法的性能。
四? ?回溯算法例題之N皇后問題
按照國際象棋的規則,皇后可以攻擊與之處在同一行或同一列或同一斜線上的棋子。n?皇后問題?研究的是如何將?
n?個皇后放置在?n×n?的棋盤上,并且使皇后彼此之間不能相互攻擊。給你一個整數?
n?,返回所有不同的?n?皇后問題?的解決方案。每一種解法包含一個不同的?n 皇后問題?的棋子放置方案,該方案中?'Q'?和?'.'?分別代表了皇后和空位。
4*4的棋盤擺放結果如下:

解題思路:
定義一個 N × N 的棋盤,使用一個二維數組或其他數據結構表示。初始化棋盤的所有位置為空。
從第一行開始,逐行放置皇后。對于每一行,遍歷該行的每一個位置,嘗試將皇后放置在當前位置。
在放置皇后之前,檢查是否滿足以下條件:
- 當前位置的同一列沒有其他皇后。
- 當前位置的左上方和右上方(對角線)沒有其他皇后。
如果滿足上述條件,將皇后放置在當前位置,并將該位置標記為已占用。
繼續遞歸地處理下一行,重復步驟 3 和步驟 4。
如果已經放置了 N 個皇后,表示找到了一個可行解,將該解保存起來。
回溯到上一步,撤銷對當前位置的選擇,繼續嘗試下一個位置。
當所有的位置都嘗試完畢或者已經找到了所有的可行解時,算法結束。
返回所有的可行解。
? ? 我們先以3*3的棋盤來看它的解空間,如圖所示:
不難看出解空間對應的是樹的結構,我們可以套用模板進行解決:
void Backtrack(char bord[][N],int n,int row){if(row>=n){//遞歸出口print(bord,n);//如果滿足直接打印結果count++;//用來記錄解的數量printf("\n");return ;}else{for(int colum=0;colum<n;colum++){//橫向遍歷if(isselect(bord,row,colum,n)){//如果滿足放置條件bord[row][colum] = 'Q';Backtrack(bord,n,row+1);//進行遞歸,選擇下一行的格子bord[row][colum] = '*';//回溯}}}
}?【完整代碼】
#include <stdio.h>
#include <stdbool.h>
#define N 100int count=0;
void print(char bord[][N],int n){for(int i=0;i<n;i++){for(int j=0;j<n;j++){if(bord[i][j] == 'Q'){printf(" Q");}else{printf(" *");} }printf("\n");}
}bool isselect(char bord[][N], int row, int colum,int n) {for(int j=0;j<row;j++){//判斷列if(bord[j][colum]=='Q'){return false;}}for(int i=row,j=colum;i>=0&&j>=0;i--,j--){//判斷左上角if(bord[i][j]=='Q'){return false;}}for(int i=row,j=colum;i>=0&&j<n;i--,j++){//判斷右上角if(bord[i][j]=='Q'){return false;}}return true;}void Backtrack(char bord[][N],int n,int row){if(row>=n){print(bord,n);count++;printf("\n");return ;}else{for(int colum=0;colum<n;colum++){if(isselect(bord,row,colum,n)){bord[row][colum] = 'Q';Backtrack(bord,n,row+1);bord[row][colum] = '*';}}}
}int main()
{int n;printf("請輸入皇后個數:\n");scanf("%d",&n);char bord[N][N]={'*'};printf("皇后擺放形式如下:\n");Backtrack(bord,n,0);printf("%d后問題共有%d種擺放方案 ",n,count);return 0;
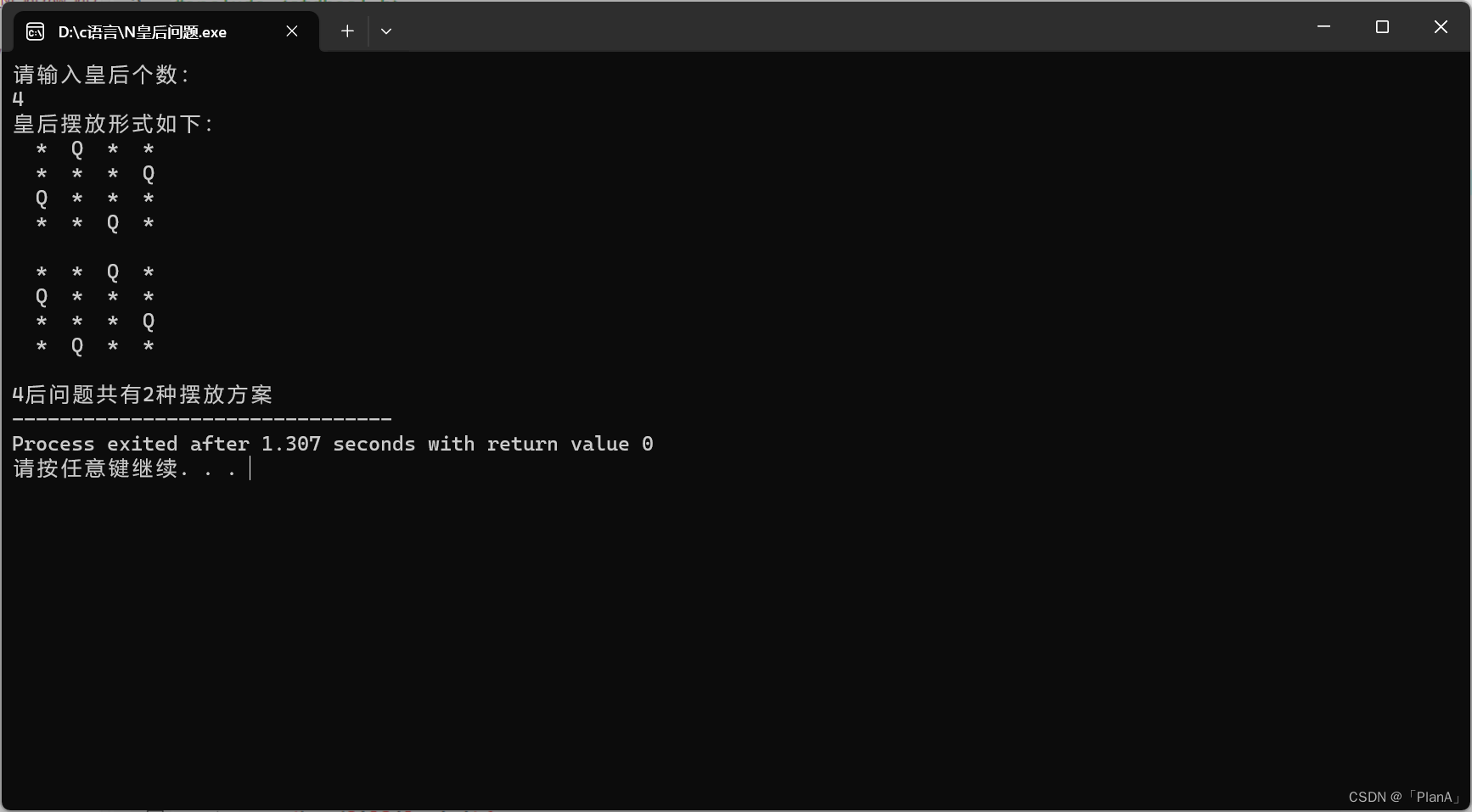
}【運行效果】

部分資料參考:代碼隨想錄;?






 函數 ))












