目錄

一、題目要求

二、解題思路

（1）狀態表示

（2）狀態轉移方程

（3）初始化dp表

（4）填表順序

（5）返回值

三、代碼

---

一、題目要求

174. 地下城游戲

惡魔們抓住了公主并將她關在了地下城?dungeon?的?右下角?。地下城是由?m x n?個房間組成的二維網格。我們英勇的騎士最初被安置在?左上角?的房間里，他必須穿過地下城并通過對抗惡魔來拯救公主。

騎士的初始健康點數為一個正整數。如果他的健康點數在某一時刻降至 0 或以下，他會立即死亡。

有些房間由惡魔守衛，因此騎士在進入這些房間時會失去健康點數（若房間里的值為負整數，則表示騎士將損失健康點數）；其他房間要么是空的（房間里的值為?0），要么包含增加騎士健康點數的魔法球（若房間里的值為正整數，則表示騎士將增加健康點數）。

為了盡快解救公主，騎士決定每次只?向右?或?向下?移動一步。

返回確保騎士能夠拯救到公主所需的最低初始健康點數。

注意：任何房間都可能對騎士的健康點數造成威脅，也可能增加騎士的健康點數，包括騎士進入的左上角房間以及公主被監禁的右下角房間。

示例 1：

輸入：dungeon = [[-2,-3,3],[-5,-10,1],[10,30,-5]]
輸出：7
解釋：如果騎士遵循最佳路徑：右 -> 右 -> 下 -> 下 ，則騎士的初始健康點數至少為 7 。

示例 2：

輸入：dungeon = [[0]]
輸出：1

二、解題思路

這題我們用到動態規劃的思想，分析題目，我們要從左上角走到右下角，求我們最小初始健康點數是多少。

（1）狀態表示

按往常經驗，我們喜歡以某個點為終點，填這個位置在dp表中的值是多少，因為在這里，如果以某個點為終點，從前面到這個位置所需要的最小健康點數，就是前面消耗健康點數到這個位置還剩1個健康點數，但到這個位置還剩一個健康點數，要是沒到右下角呢，還要走好多步，肯定是還沒到右下角就已經死掉了。

所以，這里的狀態表示：定義以某個位置為起點，到達右下角所需要的最小健康點數。

（2）狀態轉移方程

如圖：

我們想在dp表的四角星位置放值，放的是在原表中從四角星位置到右下角所需最小健康點數，那么，我們知道每個dp表放的都是當前位置到右下角所需健康的最小點數，設當前點數為x，要能從當前位置走到右下角，那么走到下一個位置時的位置，還有的點數要大于等于下一個位置的點數，設原表為d，有一個新建出的dp表，

所以我們推導出：x + d[ i ][ j ] >= dp[ i + 1 ][ j ] 或?x + d[ i ][ j ] >= dp[ i ][ j + 1 ]

所以，x =?dp[ i + 1 ][ j ] -?d[ i ][ j ] 或?x =?dp[ i ][ j + 1 ] -?d[ i ][ j ]

那么我們就要就要從右邊或者下邊，拿一個點數最小的值，走到下一步還需要的健康點數，當然是少的符合題目要求。

合并：x = min（dp[ i + 1 ][ j ]，dp[ i ][ j + 1 ]） - d[ i ][ j ]

特殊情況：當前位置如果是一個很大的正整數，也就是一個大血包，那么x就會算出負數，這時候就不符合我們的預期了，因為當前位置的點數是負數，也可以走到右下角，就不符合題目要求了，負數早就死了，所以我們當前x值大于0時，就不做處理，x還是原來的值，當x值小于等于0時，當前位置就放一個1，至少有血還能繼續往下走。

推出：當前位置的值：max（1，x）

（3）初始化dp表

根據我們定義的狀態表示，我們要知道下面和左邊的dp表值，才能推出當前的dp表值，所以最后一行和最后一列可能會數組越界，我們多加最后一行和最后一列，并且兩個位置初始化為1，其他位置初始化為正無窮，如圖：

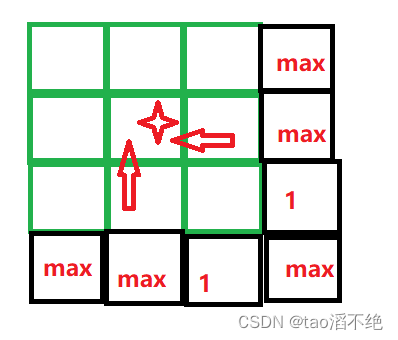
因為，騎士要到右下角，最后至少必須要有1個健康點數，才能到右下角，說明到右下角值至少需要1個健康點數，而其他位置初始化為正無窮是為了不影響最后一行和最后一列填表，比如最后一行，處除了右下角，只能往往右邊走，最后一列，只能往下走。所以得到的是右邊的dp值，右邊的值肯定比正無窮小。

（4）填表順序

從右到左，從下到上

（5）返回值

return dp[0][0]

三、代碼

class Solution {public int calculateMinimumHP(int[][] dungeon) {//1、創建dp表int row = dungeon.length;//行int col = dungeon[0].length;//列int[][] dp = new int[row + 1][col + 1];//2、初始化dp表for(int i = 0; i < col + 1; i++) {//初始化最后一行dp[row][i] = Integer.MAX_VALUE;}dp[row][col - 1] = 1;//最后一行的特殊位置for(int i = 0; i < row + 1; i ++) {//初始化最后一列dp[i][col] = Integer.MAX_VALUE;}dp[row - 1][col] = 1;//最后一列的特殊位置//3、填dp表(順序：從右到左，從下到上)for(int i = row - 1; i >= 0; i--) {for(int j = col - 1; j >= 0; j--) {int min = Math.min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j];dp[i][j] = Math.max(1, min);}}//4、返回值return dp[0][0];}
}