上一篇

人工智能原理復習–確定性推理

搜索概述

問題求解分為兩大類：知識貧乏系統（依靠搜索技術解決）、知識豐富系統（依靠推理技術）
兩大類搜索技術：

1. 一般圖搜索、啟發式搜索
2. 基于問題規約的與或圖搜索

求解問題包括：1. 目標表示 2.搜索 3.執行
初始狀態集合和操作符集合定義了問題的搜索空間

搜索策略評價標準：

1. 完備性
2. 最優性
3. 時間復雜性
4. 空間復雜性

一般圖搜索

狀態空間搜索是一般圖搜索的代表形式，用狀態空間搜索來求解問題的系統均定義一個狀態空間，并通過適當的搜索算法在態空間中搜索解答路徑。

狀態空間表示法：定義狀態的描述形式，將一切狀態表示出來，再定義一組操作算子，通過他們將問題由一種狀態轉變為另一個狀態。問題求解過程就是不斷通過操作作用于狀態的過程，得到操作狀態到目標狀態所用的操作序列的過程。

而使用操作最少或較少的解稱為最優解，采用不同的搜索策略得到的結果順序也可能不同。



狀態空間可表示成二元組(S, O)：
S:表示所有可能到達的合法狀態構成的集合
O:表示操作算子的集合
狀態就用一個矢量來表示某一時刻問題現狀的快照

狀態空間圖：1. 結點：狀態 2. 有向弧：狀態的變遷 3.弧上的標簽：導致狀態變遷的操作算子
問題的狀態空間是一個表示該問題的所有可能狀態及其變遷的有向圖

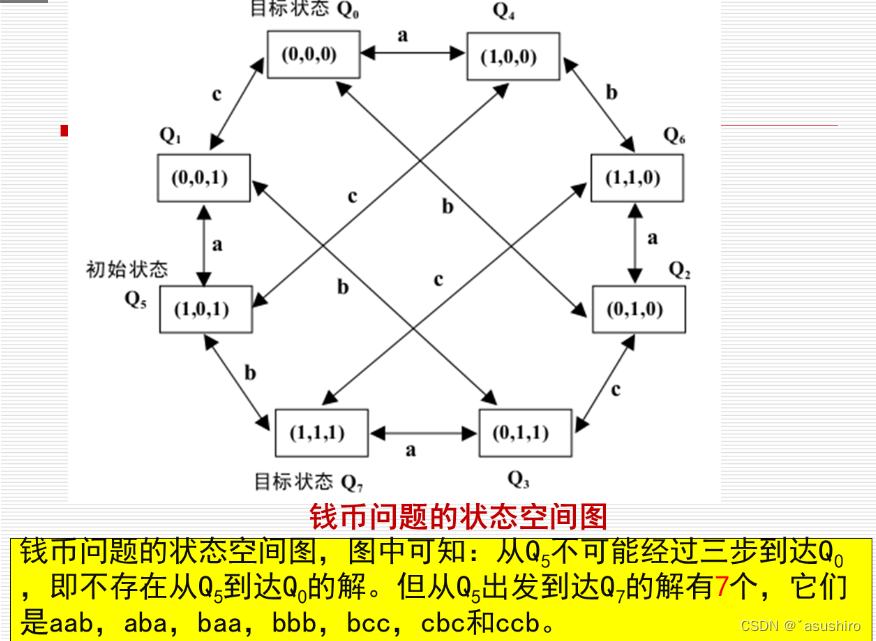
狀態空間表示例子

1. 狀態：(1, 0, 1) 表示狀態位（正，反，正）
2. 操作算子：
   a:表示翻轉第一個錢幣
   b:表示翻轉第二個錢幣
   c:表示翻轉第三個錢幣

傳教士與野人問題
描述：N個傳教士帶領N個野人劃船過河；
需要滿足三個約束條件：

1. 船上人數不得超過載重限量，設為K個人
2. 任意時刻（包括兩岸、船上）野人數量不得超過傳教士
3. 允許在河的某一岸或者在船上只有野人而沒有傳教士

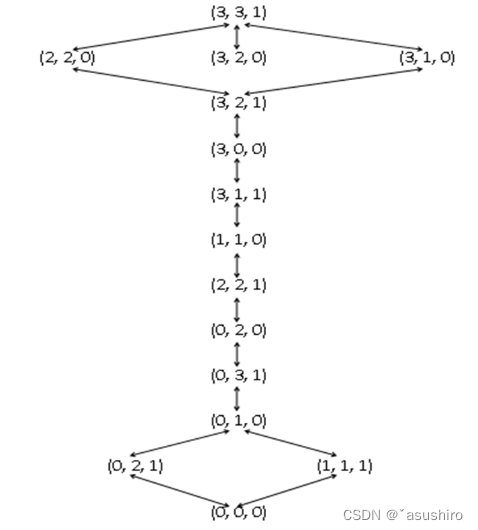
求解當N = 3，K = 2時的狀態空間有向圖
解：
狀態表示：
（m, c, b）表示(傳教士在左岸的實際數量，野人在左岸實際數量，船是否停在左岸（0/1）)
共有 4 x 4 x 2 = 32中狀態
其中合法狀態：

1. 左岸傳教士和右岸傳教士人數大于野人
   m = 1, c = 1; m = 2, c = 2;
2. 左岸只有野人沒有傳教士
   m = 0, c = 0, 1, 2, 3
3. 左岸只有傳教士沒有野人
   m = 3, c = 0, 1, 2, 3

不可能達到的合法狀態：

• (0, 0, 1）人過去了船飄了回去
• (0, 3, 0) 傳教士過去不帶野人不符合目的
• (3, 0, 1) 野人過去但是船回來了
• (3, 3, 0) 只有船過去了

操作算子：
L(x, y)表示從左岸向右岸劃船,x表示傳教士人數，y表示野人數量
R(x, y)表示從右岸向左岸劃船,x表示傳教士人數，y表示野人數量

x, y取值為(1, 0) , (2, 0), (1, 1), (0, 1), (0, 2)
可以看出野人自己也會劃船

而整個狀態空間搜索可以用五元組表示：
SE=(S,O,E,I,G)
E–搜索引擎（搜索策略/算法）
I–問題的初始狀態
G–問題的目標狀態

基本思想：通過搜索引擎E尋找一個操作算子的調用序列，使問題從初始狀態I變遷到目標狀態G之一。
解答路徑就是從初始狀態到目標狀態的操作算子的調用序列。

搜索樹：
一般圖的搜索過程是或圖，操作算子之間時一種“或”的關系

搜索術語：

1. 節點深度：根節點指示初始狀態，不同情況對應的操作順序長度
2. 節點擴展：應用操作算子將上一狀態轉變到下一狀態而拓展出節點
3. 路徑：要求路徑是無環的
4. 路徑代價：

符號說明：
s – 初始狀態節點
G – 搜索圖
OPEN – 存放待擴展節點的表
CLOSE – 存放已被擴展的結點的表
MOVE-FIRST(OPEN) – 取OPEN表首的節點作為當前要被擴展的節點n同時將結點n移至CLOSE表

分為兩個階段：

1. 初始化
   • 建立只包含初始結點s的搜索圖G:={s}
   • OPEN:={s}
   • CLOSE:={}
2. 搜索循環
   • MOVE-FIRST(OPEN)-取出OPEN表首的結點n作為擴展節點，同時將其移到close表
   • 拓展n的子節點，插入圖G和OPEN表
   • 適當標記和修改指針
   • 排序OPEN表

擴展的節點分為3類：

1. 全新節點(直接加入到OPEN表中)
2. 已出現在OPEN表中的節點（在OPEN表排序，找最短搜索順序）
3. 已出現在CLOSE表中的節點（當前確定的路徑）

盲目搜索

提高搜索效率的關鍵是優化OPEN表中節點的排序方式

BFS
擴展當前節點后生成的子節點總是置于OPEN表的后端，及OPEN表作為隊列，先進先出，是搜索優先向橫向方向發展。

性質：

1. 當問題有解時，一定能找到解
2. 當問題為單位代價時，有解時，一定能找到最優解
3. 效率較低，具有通用性，屬于圖搜索方法

優缺點：

1. 找到目標節點的路徑最短
2. 時間和空間復雜度都比較高，無用節點較多

DFS
擴展當前節點后生成的子節點總是置于OPEN表的前端，即OPEN表作為棧，后進后出，使搜索優先向縱深方向發展。

由于人工智能中一條路徑的深度不可測，所以這樣做不一定找得到最佳解，甚至可能找不到解，所以為了保證能找到解所以應加上深度界限(有界DFS)，或者采取不斷加大深度界限的辦法，反復搜索(迭代加深DFS)。

DFS的性質：

• 不能保證找到最優解
• 當深度限制不合理時，可能找不到解
• 最壞情況下相當于窮舉，是一個通用的與問題無關的方法

優缺點：
優點：比BFS使用較少的空間
缺點：既不是完備的，也不是最優的

BFS與DFS的比較

	DFS	BFS
適用場合	當問題有多個解且只需要找到其中一個時，往往對深度進行限制	確保搜索到的是最短路徑
共同優缺點	優點：不需要設計排序方法，簡單易行,適用于復雜度不高的問題	缺點：節點排序的盲目性，白白搜索了大量無關的狀態節點

有界DFS
按深度優先算法進行，但是要給深度一個限制

深度dm很重要，當dm過小時可能找不到解是不完備的，當dm過大時，搜索過程會產生過多的無用節點，即浪費了計算機資源，又降低了搜索效率

主要問題就是深度限制值dm的選取

迭代加深搜索
先任意給定一個較小的數作dm，然后按有界深度算法搜索，若在此深度限制內找到了解，則算法結束，否則增大深度限制dm，繼續搜索。

相對于整個樹的結點來說，距離根節點的節點就是很少的，對這些節點反復擴展對于整個樹來說是很小的，所以相對看了負擔實際很小。

四種方法的比較

• 四種方法都可以用于生成和測試后面改進的算法的性能
• 寬度優先搜索需要指數數量的空間，深度優先搜索的空間復雜度和最大搜索深度呈線性關系
• 迭代加深搜索對一顆深度受控的樹采用深度優先的搜索，它結合了寬度優先和深度優先的優點，和寬度優先搜索一樣，它是最優的，也是完備的。但對空間要求和深度優先搜索一樣是適中的。

標準	寬度優先	深度優先	有界深度	迭代加深
時間	$b^d$	$b^m$	$b^{dm}$	$b^d$
空間	$b^d$	$b?m$	$b?dm$	$bd$
最優	是	否	否	是
完備	是	否	如果$dm>d$	是

b是分支系數，d是解答深度，m是搜索樹的最大深度，dm是深度限制

下一篇

未完待續