1.貝葉斯公式

貝葉斯理論的思路是，在主觀判斷的基礎上，先估計一個值（先驗概率），然后根據觀察的新信息不斷修正(可能性函數)。

P(A)：沒有數據B的支持下，A發生的概率，也叫做先驗概率。這完全是根據經驗做出的判斷，這也是前面說的貝葉斯公式的主觀因素部分。

P(A|B)：在數據B的支持下，A發生的概率，也叫后驗概率。即在B事件發生之后，我們對A事件概率的重新評估。

P(B|A)：給定某參數A的概率分布：也叫似然函數。這是一個調整因子，即新信息B帶來的調整，作用是使得先驗概率更接近真實概率。至于新信息帶來的調整作用大不大，還得看因子的值大不大。

假如我在大學校園中隨機找出一個人B，身高170，體重60。P(A)是大學中男生的占比，是先驗概率。

那么從所有男生中選出身高170，體重60的人的概率就是似然概率，也就是從男生的分布（男生的概率密度函數）中得到B的概率。

那么選出的這個人B是男生的可能性就是后驗概率P(A|B)。

無監督學習中的一個核心問題就是——密度估計問題。要訓練出一個模型，使該模型的概率密度函數和真實的訓練數據分布盡可能相似。

2.生成模型分類

無監督學習兩種典型思路：

1.顯式密度估計：顯式的定義并求解分布Pmodel(x)。分布的方程是能夠寫出來定義出來的。可以算出特征空間中選取的點生成的樣本可信度，概率值。

2.隱式的密度估計：學習一個模型Pmodel(x)，無需顯式的公式定義。只能夠生成樣本。只會產生特征空間中概率比較大，與真圖相似的點。

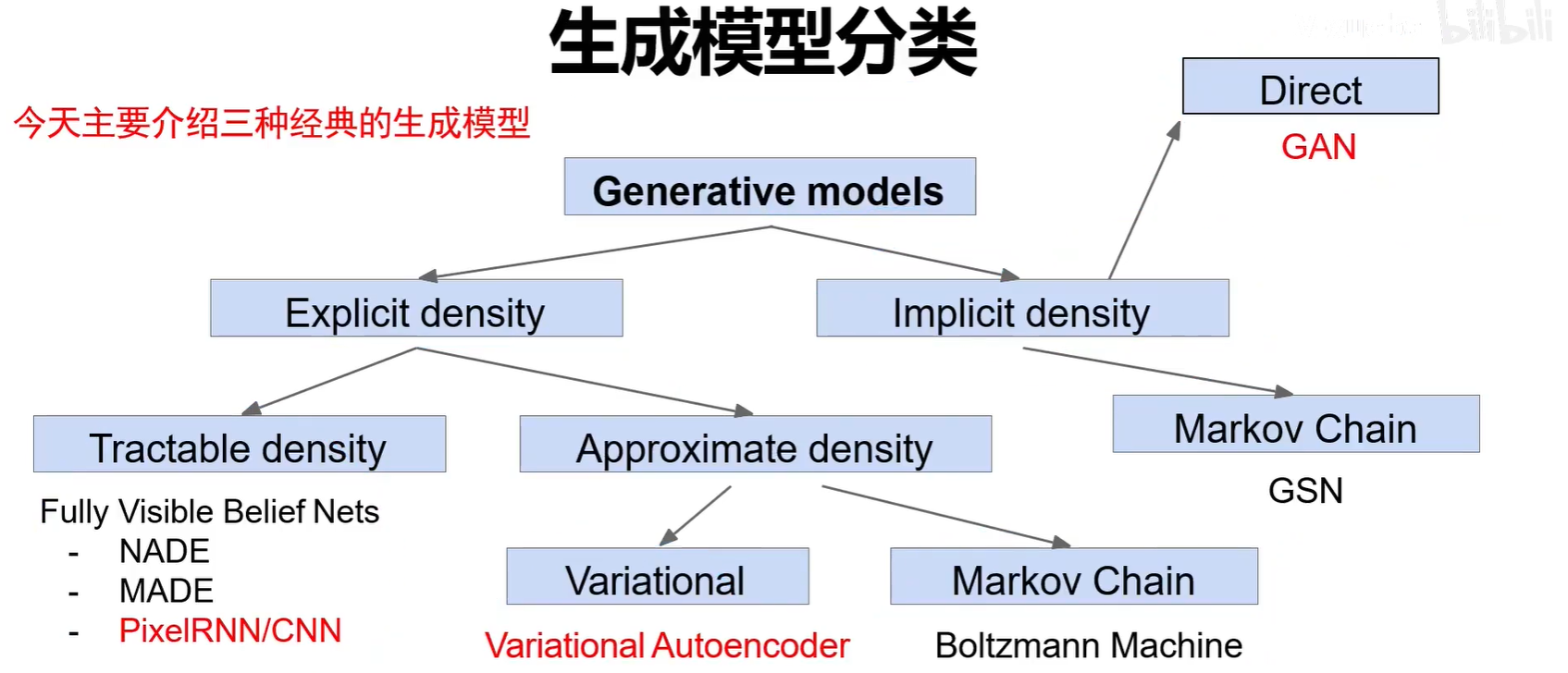
生成模型主要分為顯示概率密度-可求解，顯式概率密度-可近似和隱式概率密度。

2.1 PixelRNN與PixelCNN

?

?

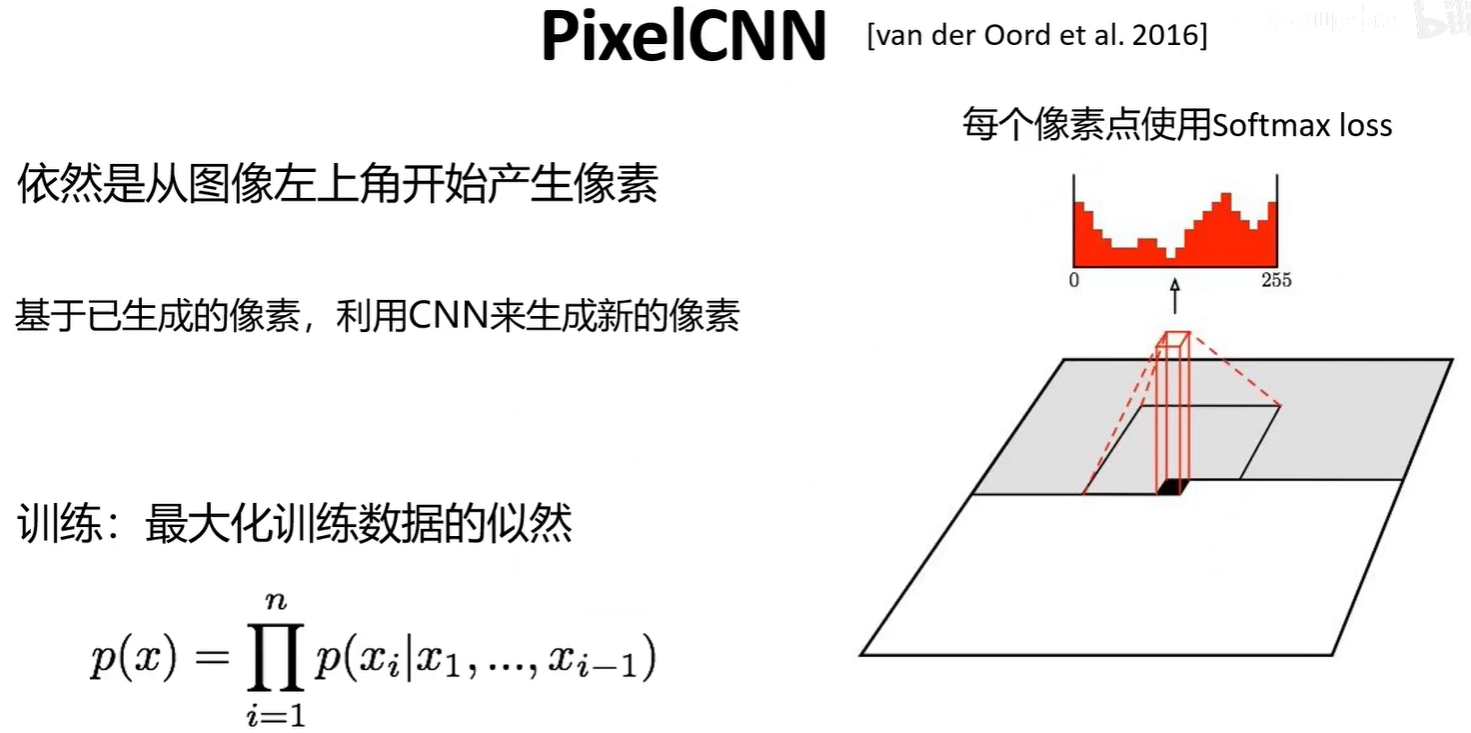
PixelRNN與PixelCNN是前面的像素生成后，來預測下一個像素的值，在知道前面的像素值后，該像素值的概率分布（0-255的每個值的概率）是可以計算出來的。

2.2 VAE

?

?

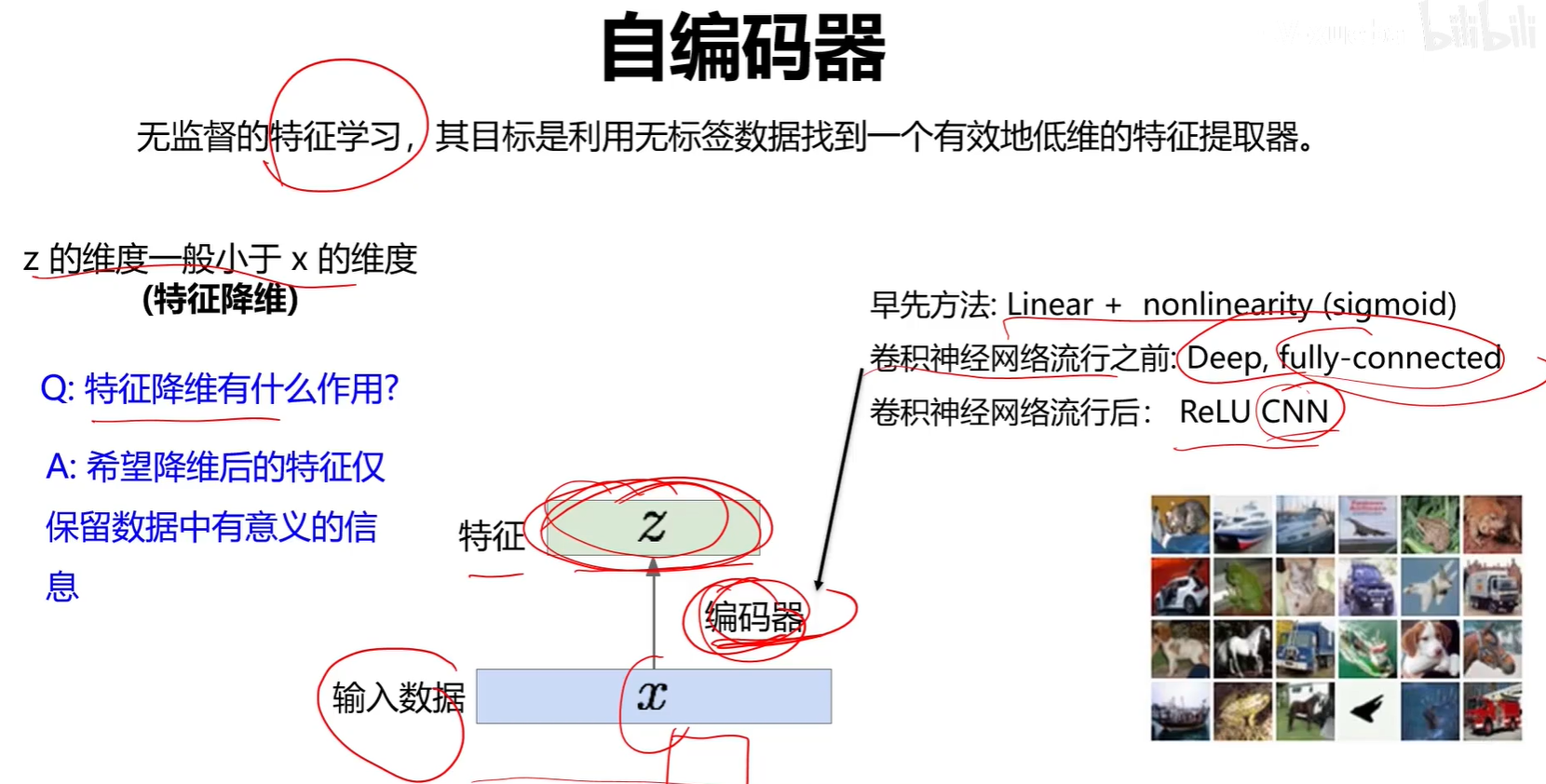
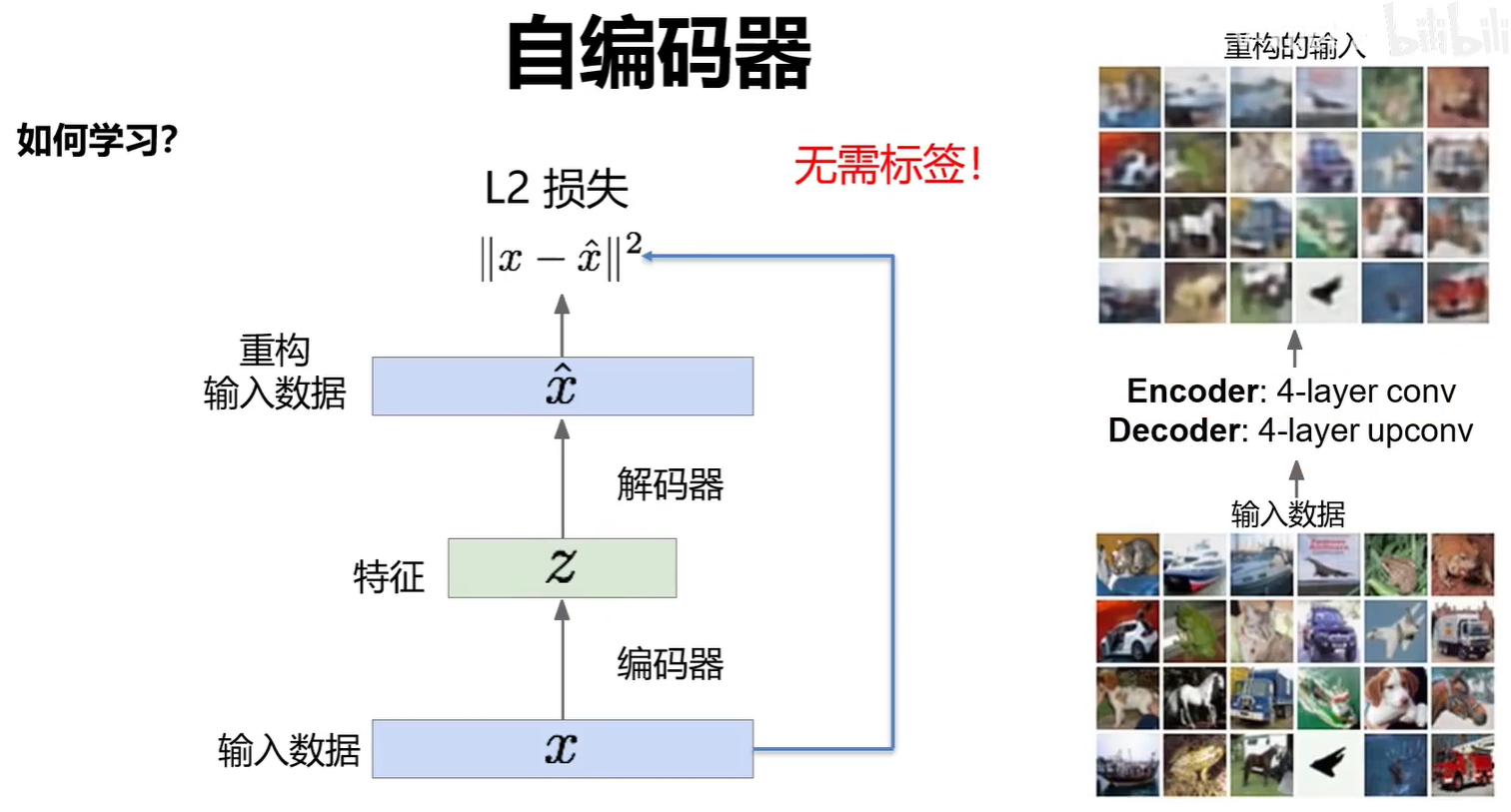
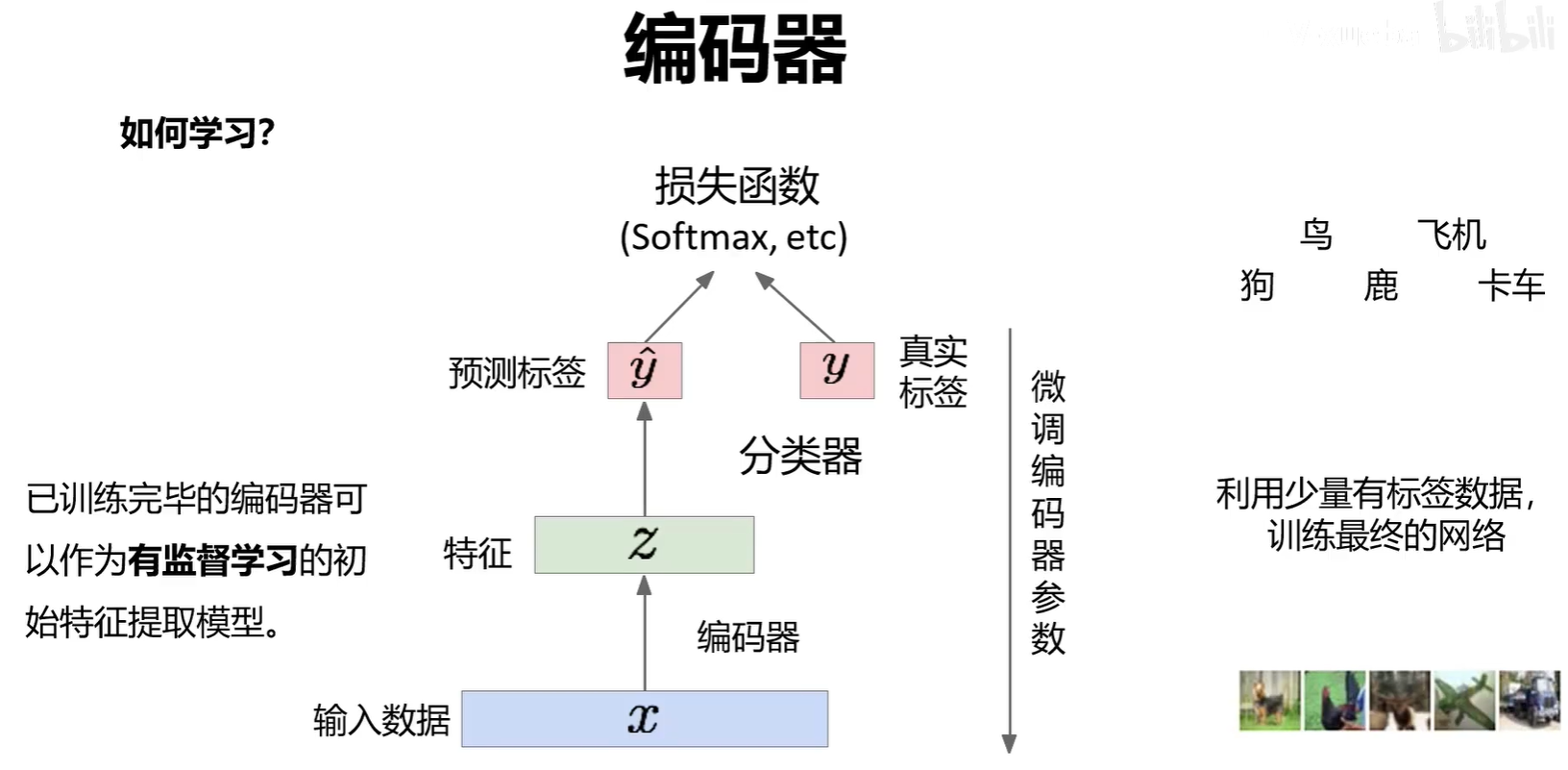
編碼器可以單獨作為一個特征提取網絡來進行分類任務。

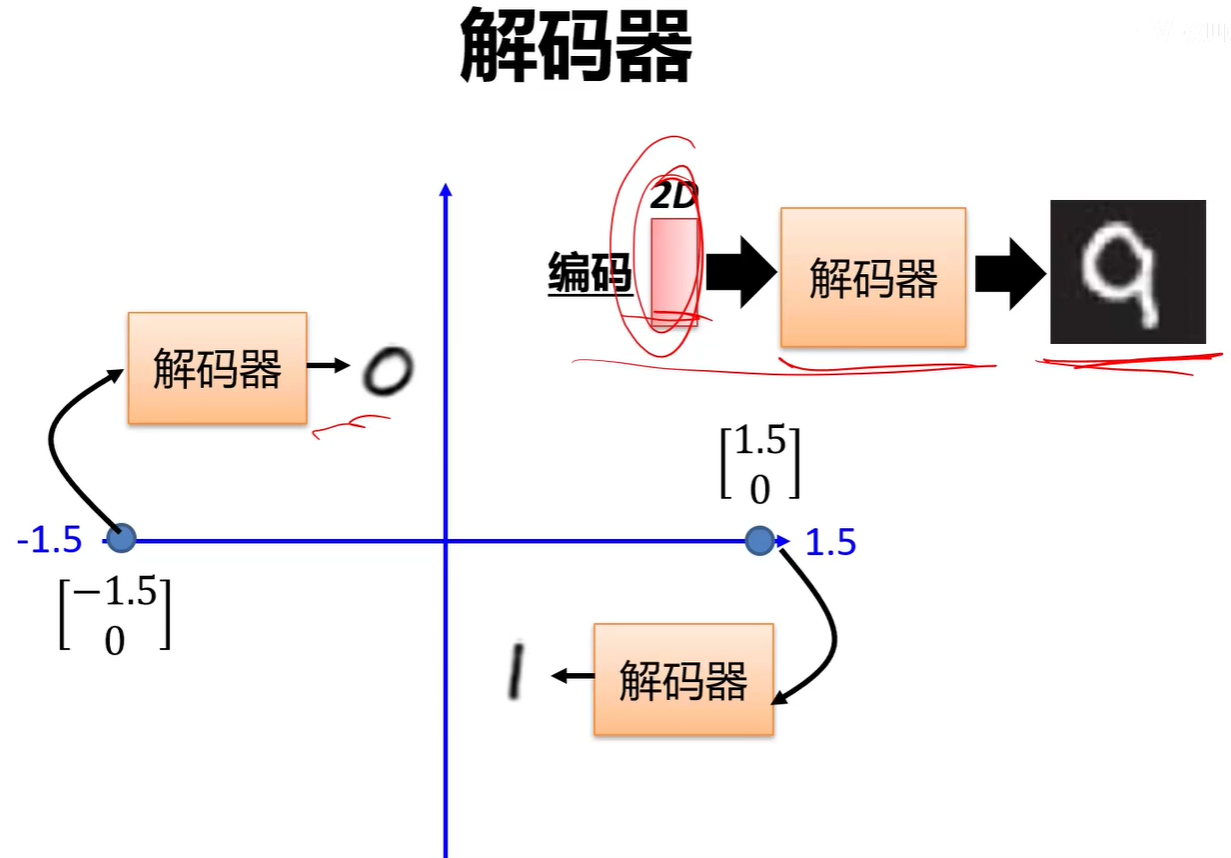
解碼器可以單獨分割出來作為一個圖像生成器。