本講為考前復習課，考試范圍就是 Ax=b 這個單元，重點是長方形矩陣，與此相關的概念包括零空間、左零空間、秩、向量空間、子空間，特別是四個基本子空間。當矩陣為可逆的方陣時，很多性質是一目了然的，但是對于長方形矩陣則需要多加注意。

問題一

向量 u，v 和 w 是 R7空間中的非零向量。它們張成了 R7空間中的一個子空間，那么這個子空間的維數可能是多少？
解答：1，2 或者 3。空間的基的個數不超過 3 個，所以其維數也不會超過 3。因為是非零向量，所以不能是 0。

問題二

給定矩陣 U 為 5 X 3 階梯型矩陣，其秩 r=3。
1.求 U 的零空間 N(U)
解答：因為列數為 3 且秩為 3，其列向量線性無關，則 Ux=0 只有零解，所以其零空間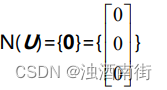

5.C 的秩？
解答：6，B 的秩為 3。
6.求 C 左零空間的維數 dim N($C^T$)?
解答：m=10 而 r=6，所以 dim N($C^T$)=4。

問題三

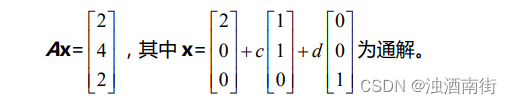
1.矩陣 A 的形狀？
解答：矩陣 A 為 3 X 3 矩陣，因為 x 的分量數即為 A 的列數，而 b 的分量數為A 的行數。
2.矩陣 A 的行空間的維數？
解答：從通解的形式可以看出 A 零空間的維數為 2，則其行空間的維數為 3-2=1。

本題中矩陣的秩為 1，因此零空間很大。請注意系數矩陣滿秩的情況，我們曾經花了不少時間進行討論。
小問題
1.A 是方陣，零空間只有零向量 0，AT的零空間？
解答：AT的零空間也只有零向量。
2.所有的 5 X 5 可逆矩陣，是否構成 5 X 5 矩陣空間的子空間？
解答：不行，不包含零矩陣 0，不是子空間。順便說一下奇異陣也不是一個子空間。

4.判斷：方程組 Ax=b 具有 n 個方程 n 個未知數，若矩陣 A 的列向量線性無關，則b 取任意向量，方程均有解。
解答：是，A 為可逆矩陣，所以 x=$A^{?1}$b 是唯一解。

問題四

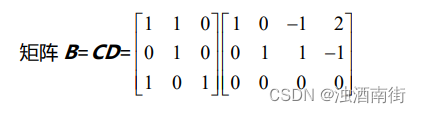
1.給出矩陣 B 零空間的一組基？
解答：因為矩陣 C 為可逆矩陣，因此矩陣 B 零空間與矩陣 D 的零空間相同。


小問題
1.判斷：A 為方陣，則它的行空間和列空間相同？
解答：否，只是空間的維數相等，但空間不一定相同。反例
$$B=\left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right]$$

2.判斷：矩陣 A 和-A 的四個子空間相同？
解答：是，相同。
3.判斷：如果 A 和 B 的四個子空間相同，則 A 一定是 B 的倍數？
解答：錯誤，A 和 B 的可以為同階可逆方陣。
4.如果我們對矩陣 A 中的兩行做行交換，四個子空間中不變的是哪些？
解答：是行空間和零空間。