【C++】：搜索二叉樹

朋友們、伙計們，我們又見面了，本期來給大家解讀一下有關多態的知識點，如果看完之后對你有一定的啟發，那么請留下你的三連，祝大家心想事成！

C 語 言 專 欄：C語言：從入門到精通

數據結構專欄：數據結構

個? 人? 主? 頁?：stackY、

C + + 專 欄? ?：C++

Linux 專?欄? ：Linux

??

目錄

1. 搜索二叉樹

1.1 概念

1.2 搜索二叉樹操作

2. 模擬實現搜索二叉樹?

2.1 非遞歸版本

2.1.1 基本構造

2.1.2 插入

2.1.3 刪除

2.1.4 查找

2.2 遞歸版本

2.2.1 插入

2.2.2 刪除

2.2.3 查找

2.2.4?中序遍歷

3. 完整代碼

1. 搜索二叉樹

1.1 概念

二叉搜索樹又稱二叉排序樹，它或者是一棵空樹，或者是具有以下性質的二叉樹:

  • 若它的左子樹不為空，則左子樹上所有節點的值都小于根節點的值
  • 若它的右子樹不為空，則右子樹上所有節點的值都大于根節點的值
  • 它的左右子樹也分別為二叉搜索樹

1.2 搜索二叉樹操作

?

1. 二叉樹的查找

a、從根開始比較，查找，比根大則往右邊走查找，比根小則往左邊走查找。
b、最多查找高度次，走到空，還沒找到，這個值不存在。

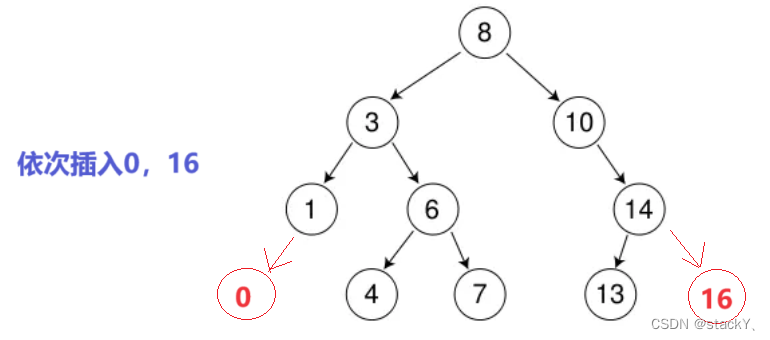
2. 二叉樹的插入

插入的具體過程如下：
a. 樹為空，則直接新增節點，賦值給root指針
b. 樹不空，按二叉搜索樹性質查找插入位置，插入新節點

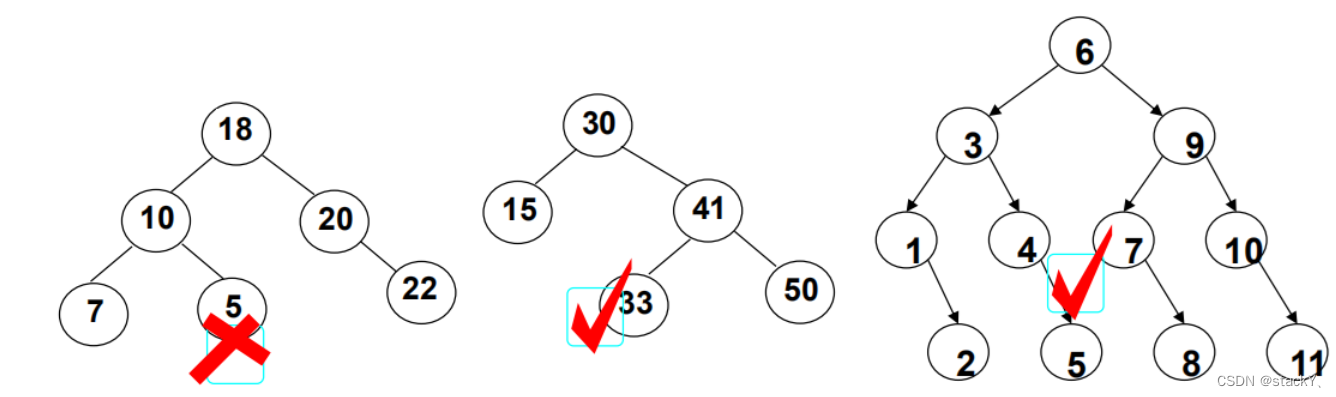
3. 二叉樹的刪除?

首先查找元素是否在二叉搜索樹中，如果不存在，則返回, 否則要刪除的結點可能分下面四種情況：
a. 要刪除的結點無孩子結點
b. 要刪除的結點只有左孩子結點
c. 要刪除的結點只有右孩子結點
d. 要刪除的結點有左、右孩子結點

2. 模擬實現搜索二叉樹?

搜索二叉樹有兩種模型：

1. Key模型：節點中只存在一個值key，并且這個值不可以修改，比如后面學習到的set

2. Key_Value模型：節點中存在兩個值，一個是key，不可修改，另一個是與key對應的value，可以修改，比如后面學習到的map

在這里我們只實現Key模型的搜索二叉樹

2.1 非遞歸版本

2.1.1 基本構造
//節點
template<class K>
struct BSTreeNode
{BSTreeNode* _left;BSTreeNode* _right;K _key;//構造BSTreeNode(const K& key):_left(nullptr),_right(nullptr),_key(key){}
};//搜索二叉樹
template<class K>
class BSTree
{
public:typedef BSTreeNode<K> Node;//構造BSTree() //給定了缺省值{}//拷貝構造BSTree(const BSTree<K>& tmp){_root = Copy(tmp._root);}//operator=BSTree<K> operator=(BSTree<K> tmp){swap(_root, tmp._root);return *this;}//析構~BSTree(){Destroy(_root);}
private://遞歸拷貝左右子樹Node* Copy(Node* root){if (root == nullptr)return nullptr;Node* newNode = new Node(root->_key);newNode->_left = Copy(root->_left);newNode->_right = Copy(root->_right);return newNode;}//后序遍歷刪除void Destroy(Node*& root){if (root == nullptr){return;}Destroy(root->_left);Destroy(root->_right);delete root;root = nullptr;}private:Node* _root = nullptr;  //缺省值給空即可
};
2.1.2 插入

插入時如果為空直接插入即可，若存在節點，需要先進行判斷，比根節點大的插入到它的右子樹，比根節點小的插入左子樹即可，這時需要注意的插入的節點需要與它的父節點進行鏈接，這時在往下比較的過程中就需要記錄一下它的父節點。

//插入bool Insert(const K& key){//如果為空可以直接插入鏈接if (_root == nullptr){_root = new Node(key);return true;}//記錄父節點Node* parent = nullptr;Node* cur = _root;//遍歷找到合適的節點進行插入鏈接while (cur){parent = cur;if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}elsereturn false;}//鏈接cur = new Node(key);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}
2.1.3 刪除

首先找到需要刪除的節點，刪除的時候需要注意分下面幾種情況：

  • 左子樹為空，可以直接刪除
  • 右子樹為空，可以直接刪除
  • 左右子樹都不為空需要使用替換法刪除
  • 替換法：使用左子樹最大的節點替換需要刪除的節點，或者使用右子樹最小的節點替換需要刪除的節點，替換之后直接刪除被替換的節點即可完成刪除。
  • 需要注意的是在這個過程中需要記錄父節點，在刪除之后需要及時鏈接，并且要注意的是刪除的節點是根節點的時候可以直接將它的左右子樹直接鏈接。
//刪除bool Erase(const K& key){Node* cur = _root;//記錄父親Node* parent = nullptr;while (cur){//找到要刪除的keyif (cur->_key > key){//更新父親parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else{//開始刪除if (cur->_left == nullptr) //左為空  //直接刪除{//先判斷是否為根節點if (cur == _root){_root = cur->_right;}else  //不為根節點{if (cur == parent->_left) {parent->_left = cur->_right;}else if (cur == parent->_right){parent->_right = cur->_right;}}delete cur;}else if (cur->_right == nullptr)   //右為空{//先判斷是否為根節點if (cur == _root){_root = cur->_left;}else{if (cur == parent->_left){parent->_left = cur->_left;}else if (cur == parent->_right){parent->_right = cur->_left;}}delete cur;}else    //左右子樹都不為空  //使用替換法{Node* parent = cur;//右樹的最小節點進行替換或者左樹的最大節點Node* subRight = cur->_right;while (subRight->_left)  //找到右樹的最小節點{parent = subRight;subRight = subRight->_left;}swap(cur->_key, subRight->_key);  //替換兩個節點//將刪除節點的右樹鏈接在它的父親if (parent->_left == subRight){parent->_left = subRight->_right;}else {parent->_right = subRight->_right;}delete subRight;}return true;}}return false;}
2.1.4 查找
//查找bool Find(const K& key){Node* cur = _root;while (cur){if (cur->_key > key){cur = cur->_left;}else if (cur->_key < key){cur = cur->_right;}elsereturn true;}return false;}

2.2 遞歸版本

2.2.1 插入

遞歸插入時也需要進行一層封裝，在里面傳遞root，在這里采用引用傳參比較好，可以不用額外的鏈接，遇到空直接創建一個節點即可，直接在原數上進行操作。

//插入bool InsertR(const K& key){return _InsertR(key, _root);}bool _InsertR(const K& key, Node*& root){//樹為空直接插入即可if (root == nullptr){root = new Node(key);return true;}//遞歸左if (root->_key > key)return _InsertR(key, root->_left);else if (root->_key < key)  //遞歸右return _InsertR(key, root->_right);elsereturn false;}
2.2.2 刪除

還是采用里面封裝一層，在遞歸刪除的時候先遞歸找到要刪除的key，然后判斷它的左右子樹，如果左右子樹只存在一個可以直接進行刪除，然后將它的孩子鏈接在它的節點上，如果左右孩子均存在，使用替換法，用該節點的右子樹的最小節點進行替換，先使用循環找到該最小節點，然后與其交換，然后轉化為遞歸該節點右子樹的刪除問題即可。

//刪除bool EraseR(const K& key){return _EraseR(key, _root);}
bool _EraseR(const K& key, Node*& root){if (root == nullptr)return false;//查找keyif (root->_key < key){return _EraseR(root->_right, key);}else if (root->_key > key){return _EraseR(root->_left, key);}else  //找到了進行刪除操作{if (root->_left == nullptr)  //作為空直接刪除{Node* del = root;root = root->_right;delete del;return true;}else if (root->_right == nullptr)  //右為空也可以直接進行刪除{Node* del = root;root = root->_left;delete del;return true;}else   //左右都不為空{Node* subRight = root;  //找到右樹的最小節點while (subRight->left){subRight = subRight->_left;}swap(root->_key, subRight->_key);  //交換return _EraseR(key, root->_right);   //轉化為遞歸右子樹的子問題}}}
2.2.3 查找
//查找bool FindR(const K& key){_FindR(key, _root);}
bool _FindR(const K& key, Node* root){if (root == nullptr)return false;if (root->_key > key)return _FindR(root->_left);else if (root->_key < key)return _FindR(root->_right);elsereturn true;}
2.2.4?中序遍歷

中序遍歷時需要封裝一層，在外面不好傳遞節點，中序遍歷：左子樹、根、右子樹

	//中序遍歷void InOrder(){_InOrder(_root);cout << endl;}void _InOrder(Node* root){if (root == nullptr)return; _InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}

3. 完整代碼

#pragma once
#include <iostream>using namespace std;template<class K>
struct BSTreeNode
{BSTreeNode* _left;BSTreeNode* _right;K _key;BSTreeNode(const K& key):_left(nullptr),_right(nullptr),_key(key){}
};template<class K>
class BSTree
{
public:typedef BSTreeNode<K> Node;//構造BSTree() //給定了缺省值{}//拷貝構造BSTree(const BSTree<K>& tmp){_root = Copy(tmp._root);}//operator=BSTree<K> operator=(BSTree<K> tmp){swap(_root, tmp._root);return *this;}//析構~BSTree(){Destroy(_root);}//非遞歸版本//插入bool Insert(const K& key){//如果為空可以直接插入鏈接if (_root == nullptr){_root = new Node(key);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){parent = cur;if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}elsereturn false;}//鏈接cur = new Node(key);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}//刪除bool Erase(const K& key){Node* cur = _root;//記錄父親Node* parent = nullptr;while (cur){//找到要刪除的keyif (cur->_key > key){//更新父親parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else{//開始刪除if (cur->_left == nullptr) //左為空  //直接刪除{//先判斷是否為根節點if (cur == _root){_root = cur->_right;}else  //不為根節點{if (cur == parent->_left){parent->_left = cur->_right;}else if (cur == parent->_right){parent->_right = cur->_right;}}delete cur;}else if (cur->_right == nullptr)   //右為空{//先判斷是否為根節點if (cur == _root){_root = cur->_left;}else{if (cur == parent->_left){parent->_left = cur->_left;}else if (cur == parent->_right){parent->_right = cur->_left;}}delete cur;}else    //左右子樹都不為空  //使用替換法{Node* parent = cur;//右樹的最小節點進行替換或者左樹的最大節點Node* subRight = cur->_right;while (subRight->_left)  //找到右樹的最小節點{parent = subRight;subRight = subRight->_left;}swap(cur->_key, subRight->_key);  //替換兩個節點//將刪除節點的右樹鏈接在它的父親if (parent->_left == subRight){parent->_left = subRight->_right;}else{parent->_right = subRight->_right;}delete subRight;}return true;}}return false;}//查找bool Find(const K& key){Node* cur = _root;while (cur){if (cur->_key > key){cur = cur->_left;}else if (cur->_key < key){cur = cur->_right;}elsereturn true;}return false;}//遞歸版本//插入bool InsertR(const K& key){return _InsertR(key, _root);}//刪除bool EraseR(const K& key){return _EraseR(key, _root);}//查找bool FindR(const K& key){_FindR(key, _root);}//中序遍歷void InOrder(){_InOrder(_root);cout << endl;}private://插入bool _InsertR(const K& key, Node*& root){//樹為空直接插入即可if (root == nullptr){root = new Node(key);return true;}//遞歸左if (root->_key > key)return _InsertR(key, root->_left);else if (root->_key < key)  //遞歸右return _InsertR(key, root->_right);elsereturn false;}//刪除bool _EraseR(const K& key, Node*& root){if (root == nullptr)return false;//查找keyif (root->_key < key){return _EraseR(root->_right, key);}else if (root->_key > key){return _EraseR(root->_left, key);}else  //找到了進行刪除操作{if (root->_left == nullptr)  //作為空直接刪除{Node* del = root;root = root->_right;delete del;return true;}else if (root->_right == nullptr)  //右為空也可以直接進行刪除{Node* del = root;root = root->_left;delete del;return true;}else   //左右都不為空{Node* subRight = root;  //找到右樹的最小節點while (subRight->left){subRight = subRight->_left;}swap(root->_key, subRight->_key);  //交換return _EraseR(key, root->_right);   //轉化為遞歸右子樹的子問題}}}//查找bool _FindR(const K& key, Node* root){if (root == nullptr)return false;if (root->_key > key)return _FindR(root->_left);else if (root->_key < key)return _FindR(root->_right);elsereturn true;}//中序遍歷void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}//拷貝Node* Copy(Node* root){if (root == nullptr)return nullptr;Node* newNode = new Node(root->_key);newNode->_left = Copy(root->_left);newNode->_right = Copy(root->_right);return newNode;}//銷毀void Destroy(Node*& root){if (root == nullptr){return;}Destroy(root->_left);Destroy(root->_right);delete root;root = nullptr;}
private:Node* _root = nullptr;
};

朋友們、伙計們，美好的時光總是短暫的，我們本期的的分享就到此結束，欲知后事如何，請聽下回分解~，最后看完別忘了留下你們彌足珍貴的三連喔，感謝大家的支持！?????

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/206890.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/206890.shtml
英文地址，請注明出處：http://en.pswp.cn/news/206890.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

C語言之動態內存管理（malloc calloc realloc）

C語言之動態內存管理（malloc calloc realloc）

C語言之動態內存管理 文章目錄 C語言之動態內存管理1. 為什么要有動態內存管理2. malloc 和 free2.1 malloc2.2 free2.3 例子 3. calloc 和 realloc3.1 calloc3.2 realloc 4. 常見的動態內存錯誤4.1 對NULL指針的解引?操作4.2 對動態開辟空間的越界訪問4.3 對?動態開辟內存使…
閱讀更多...
女裝品牌網站建設的作用如何

女裝品牌網站建設的作用如何

服裝是任何人都需要的必備品&#xff0c;尤其是女裝&#xff0c;由于女性群體愛美追求時尚的心理更高&#xff0c;因此市場中有大量女裝品牌以及大量消費者&#xff0c;其規模非常高&#xff0c;眾多大小品牌林立及消費征集下&#xff0c;商家們經營也并不太容易&#xff0c;企…
閱讀更多...
Themis: Fast, Strong Order-Fairness in Byzantine Consensus

Themis: Fast, Strong Order-Fairness in Byzantine Consensus

目錄 筆記后續的研究方向摘要引言秩序井然 Themis: Fast, Strong Order-Fairness in Byzantine Consensus CCS 2023 筆記 后續的研究方向 摘要 我們介紹了Themis&#xff0c;這是一種將交易的公平排序引入&#xff08;許可的&#xff09;拜占庭共識協議的方案&#xff0c;最…
閱讀更多...
參加百度Apollo技術沙龍—感受自動駕駛的魅力

參加百度Apollo技術沙龍—感受自動駕駛的魅力

2023年12月2日下午2點&#xff0c;我有幸參加了百度Apollo技術沙龍&#xff0c;這是一個圍繞Apollo新版本Beta的全面升級展開的深度交流活動。作為一名工程師&#xff0c;我深感榮幸能夠與眾多同行和專家一同探討自動駕駛技術的快速發展 在這次沙龍中&#xff0c;我了解到Apo…
閱讀更多...
Python：核心知識點整理大全7-筆記

Python：核心知識點整理大全7-筆記

目錄 4.2.5 遺漏了冒號 4.3 創建數值列表 4.3.1 使用函數 range() 4.3.2 使用 range()創建數字列表 結果如下&#xff1a; 4.3.3 對數字列表執行簡單的統計計算 4.3.4 列表解析 4.4 使用列表的一部分 4.4.1 切片 4.4.2 遍歷切片 4.4.3 復制列表 4.2.5 遺漏了冒號 fo…
閱讀更多...
使用vue-quill-editor（富文本框）禁用粘貼圖片

使用vue-quill-editor（富文本框）禁用粘貼圖片

問題描述&#xff1a;富文本框復制粘貼未走上傳圖片接口&#xff0c;會將復制的圖片解析為base64編碼&#xff0c;為了控制這種情況可選擇禁用粘貼圖片&#xff0c;或者監聽有復制粘貼的圖片走上傳圖片接口 獲取到 quill 對象&#xff0c;可以通過 refs 或者 Quill 對象的 getI…
閱讀更多...
小程序自動更新功能

小程序自動更新功能

小程序自動更新功能 在 .vue 頁面的 script 中添加生命周期&#xff0c;在生命周期內監聽頁面信息 onLoad onLoad(options) {this.getUserInfo()this.intervalId setInterval(() > {this.getUserInfo()}, 3000);},onUnload onUnload: function() {// 在頁面卸載時清除定時…
閱讀更多...
vue的data

vue的data

類型&#xff1a;Object | Function 限制&#xff1a;組件的定義只接受 function。 詳細&#xff1a; Vue 實例的數據對象。Vue 會遞歸地把 data 的 property 轉換為 getter/setter&#xff0c;從而讓 data 的 property 能夠響應數據變化。對象必須是純粹的對象 (含有零個或多個…
閱讀更多...
DC電源模塊與節能環保的關系

DC電源模塊與節能環保的關系

BOSHIDA DC電源模塊與節能環保的關系 隨著全球能源危機的加劇&#xff0c;環保節能已經成為世界各國政府和企業發展的主要方向。在電子行業中&#xff0c; DC電源模塊的出現為環保節能做出了貢獻。DC電源模塊是一種電源供應器件&#xff0c;可將高電壓轉換為低電壓&#xff0c;…
閱讀更多...
柏林噪聲C++

柏林噪聲C++

柏林噪聲 隨機噪聲 如上圖所示隨機噪聲沒有任何規律可言&#xff0c;我們希望生成有一些意義的局部連續的隨機圖案 一維柏林噪聲 假設希望生成一段局部連續的隨機曲線&#xff0c;可以采用插值的方式&#xff1a;在固定點隨機分配y值&#xff08;一般是整數點&#xff09;&a…
閱讀更多...
【數據分析實戰】酒店行業華住集團門店分布與評分多維度分析

【數據分析實戰】酒店行業華住集團門店分布與評分多維度分析

文章目錄 1. 寫在前面2. 數據集展示3. 多維度分析3.1 門店檔次多元化&#xff1a;集團投資戰略觀察3.1.1 代碼實現3.1.2 本人淺薄理解 3.2 門店分布&#xff1a;各省市分布概覽3.2.1 代碼實現3.2.2 本人淺薄理解 3.3 門店分級評分&#xff1a;服務水平的多維度觀察3.3.1 代碼實…
閱讀更多...
F5怎么樣？從負載均衡到云原生的進階之路

F5怎么樣？從負載均衡到云原生的進階之路

從Web時代開始至云原生時代的應用服務交付的市場&#xff0c;技術與人的變化就是關注的焦點。從單純的Web負載均衡到復雜的企業應用交付&#xff0c;從單體應用到分布式、微服務架構&#xff0c;F5為企業技術架構更好、更優、更安全的運行做出了極大的努力。那么F5怎么樣&#…
閱讀更多...
Vue 循環走馬燈

Vue 循環走馬燈

1、使用 transform: translateX()&#xff0c;循環將滾動內容在容器內偏移&#xff0c;超出容器部分隱藏&#xff1b; 2、避免滾動到末尾時出現空白&#xff0c;需要預留多幾個。 3、一次循環偏移的距離scrollLoopWidth 可能受樣式影響需要做些微調&#xff0c;比如單個item的…
閱讀更多...
題目：分糖果（藍橋OJ 2928）

題目：分糖果（藍橋OJ 2928）

題目描述&#xff1a; 解題思路&#xff1a; 本題采用貪心思想 圖解 題解&#xff1a; #include<bits/stdc.h> using namespace std;const int N 1e6 9; char s[N];//寫字符串數組的一種方法,像數組一樣***int main() {int n, x;cin >> n >> x;for(int …
閱讀更多...
CSS新手入門筆記整理：元素類型相互轉換

CSS新手入門筆記整理：元素類型相互轉換

元素類型 塊元素&#xff08;block&#xff09; 獨占一行&#xff0c;排斥其他元素跟其位于同一行&#xff0c;包括塊元素和行內元素。塊元素內部可以容納其他塊元素和行內元素。可以定義 width&#xff0c;也可以定義 height。可以定義 4 個方向的 margin。 行內元素&#xf…
閱讀更多...
使用navicat（或者其他數據庫管理工具）、powerdesigner導出數據字典

使用navicat（或者其他數據庫管理工具）、powerdesigner導出數據字典

適合先有數據庫結構&#xff0c;后需要導出數據字典的情況&#xff0c;多數在發開完成交文檔或者用戶有庫的情況下 有條件的話推薦用powerdesigner導出&#xff0c;比較好看 如果用powerdesigner導出的注釋不對&#xff0c;是因為數據庫的編碼不對 1、使用navicat導出 在該數…
閱讀更多...
代碼隨想錄算法訓練營第45天| 70. 爬樓梯 （進階） 322. 零錢兌換 279.完全平方數

代碼隨想錄算法訓練營第45天| 70. 爬樓梯 （進階） 322. 零錢兌換 279.完全平方數

JAVA代碼編寫 70. 爬樓梯&#xff08;進階版) 卡碼網&#xff1a;57. 爬樓梯&#xff08;第八期模擬筆試&#xff09; 題目描述 假設你正在爬樓梯。需要 n 階你才能到達樓頂。 每次你可以爬至多m (1 < m < n)個臺階。你有多少種不同的方法可以爬到樓頂呢&#xff1f…
閱讀更多...
菜鳥學習日記（python）——推導式

菜鳥學習日記（python）——推導式

python中的推導式是一種獨特的數據處理方式&#xff0c;可以從一個數據序列去構建另一個新的數據序列的結構體。 它包括以下推導式&#xff1a; 列表&#xff08;list&#xff09;推導式字典&#xff08;dict&#xff09;推導式集合&#xff08;set&#xff09;推導式元組&am…
閱讀更多...
Multi-Cell Downlink Beamforming: Direct FP, Closed-Form FP, Weighted MMSE

Multi-Cell Downlink Beamforming: Direct FP, Closed-Form FP, Weighted MMSE

這里寫自定義目錄標題 Direct FPClosed-Form FPthe Lagrangian functionthe Lagrange dual function: maximizing the Lagrangianthe Lagrange dual problem: minimizing the Lagrange dual functionClosed-Form FP Weighted MMSE原論文 Lagrange dual5.1.1 The Lagrangian5.1.…
閱讀更多...
阿里云服務器經濟型、通用算力型、計算型、通用型、內存型實例區別及選擇參考

阿里云服務器經濟型、通用算力型、計算型、通用型、內存型實例區別及選擇參考

當我們通過阿里云的活動購買云服務器會發現&#xff0c;相同配置的云服務器往往有多個不同的實例可選&#xff0c;而且價格差別也比較大&#xff0c;例如同樣是4核8G的配置的云服務器&#xff0c;經濟型e實例活動價格只要1500.48/1年起&#xff0c;通用算力型u1實例要1795.97/1…
閱讀更多...
最新文章

Copyright @ 2022~2023