JAVA代碼編寫
70. 爬樓梯(進階版)
卡碼網:57. 爬樓梯(第八期模擬筆試)
題目描述
假設你正在爬樓梯。需要 n 階你才能到達樓頂。
每次你可以爬至多m (1 <= m < n)個臺階。你有多少種不同的方法可以爬到樓頂呢?
注意:給定 n 是一個正整數。
輸入描述
輸入共一行,包含兩個正整數,分別表示n, m
輸出描述
輸出一個整數,表示爬到樓頂的方法數。
輸入示例
3 2
輸出示例
3
提示信息
數據范圍:
1 <= m < n <= 32;
當 m = 2,n = 3 時,n = 3 這表示一共有三個臺階,m = 2 代表你每次可以爬一個臺階或者兩個臺階。
此時你有三種方法可以爬到樓頂。
1. 1 階 + 1 階 + 1 階段
2. 1 階 + 2 階
3. 2 階 + 1 階
教程:https://programmercarl.com/0070.%E7%88%AC%E6%A5%BC%E6%A2%AF%E5%AE%8C%E5%85%A8%E8%83%8C%E5%8C%85%E7%89%88%E6%9C%AC.html#%E6%80%9D%E8%B7%AF
方法一:動態規劃
思路:和70. 爬樓梯很像,基礎的是每次只能走1個或2個臺階,現在改成能走1-m中任意一個臺階。問有多少種方法走完n階樓梯。
步驟
-
定義dp數組:dp[j]: 爬到第j層樓梯,有dp[j]種方法
-
遞推公式:dp[j] = dp[j - 1] + dp[j - 2] + … +dp[j - m]
- dp[j - 1],上j-1層樓梯,有dp[j - 1]種方法,那么再1步跳一個臺階不就是dp[j]了么。
- dp[j - 2],上j-2層樓梯,有dp[j - 2]種方法,那么再2步跳兩個臺階不就是dp[j]了么。
- …
- dp[j - m],上j-m層樓梯,有dp[j - m]種方法,那么再m步跳兩個臺階不就是dp[j]了么。
可以這樣理解。因為每次只能走1個樓梯或2個樓梯…或m個樓梯,那么我們要走j個樓梯,可以從第j-m個樓梯,再走m個樓梯;…;也可以從第j-1個樓梯,再走1個樓梯。所以dp[j] = dp[j - 1] + dp[j - 2] + … +dp[j - m]
-
dp數組初始化:dp[1]=1,dp[2]=2
-
確定遍歷順序:遍歷n,再遍歷m
-
舉例推導dp數組
n=4,m=2
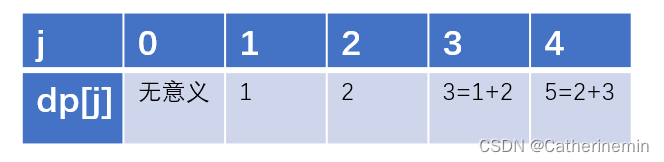
簡單來說,dp[j]等于前m個dp的和,這里的dp[4]=dp[3]+dp[2],剛好是2個的和。
復雜度分析:
- 時間復雜度:
O(n * m) - 空間復雜度:
O(n)
import java.util.Scanner;class Solution{public static void main(String [] args){Scanner sc = new Scanner(System.in);int m, n;while (sc.hasNextInt()) {// 從鍵盤輸入參數,中間用空格隔開n = sc.nextInt();m = sc.nextInt();// 求排列問題,先遍歷背包再遍歷物品int[] dp = new int[n + 1];dp[0] = 1;for (int j = 1; j <= n; j++) {for (int i = 1; i <= m; i++) {if (j - i >= 0) dp[j] += dp[j - i];}}System.out.println(dp[n]);}}
}
322. 零錢兌換
給你一個整數數組 coins ,表示不同面額的硬幣;以及一個整數 amount ,表示總金額。
計算并返回可以湊成總金額所需的 最少的硬幣個數 。如果沒有任何一種硬幣組合能組成總金額,返回 -1 。
你可以認為每種硬幣的數量是無限的。
示例 1:
輸入:coins = [1, 2, 5], amount = 11
輸出:3
解釋:11 = 5 + 5 + 1
示例 2:
輸入:coins = [2], amount = 3
輸出:-1
示例 3:
輸入:coins = [1], amount = 0
輸出:0
提示:
1 <= coins.length <= 121 <= coins[i] <= 231 - 10 <= amount <= 104
教程:https://programmercarl.com/0322.%E9%9B%B6%E9%92%B1%E5%85%91%E6%8D%A2.html
方法一:動態規劃
思路:五步曲
步驟
-
定義dp [j]:湊成和為amount的最少硬幣個數為dp[j]。
-
遞推公式:
湊足總額為j - coins[i]的最少個數為dp[j - coins[i]],那么只需要加上一個錢幣coins[i]即dp[j - coins[i]] + 1就是dp[j](考慮coins[i])
所以dp[j] 要取所有 dp[j - coins[i]] + 1 中最小的。
遞推公式:dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
-
dp數組初始化:dp[0] =0,考慮到遞推公式的特性,dp[j]必須初始化為一個最大的數,否則就會在min(dp[j - coins[i]] + 1, dp[j])比較的過程中被初始值覆蓋。
-
確定遍歷順序:
本題求錢幣最小個數,那么錢幣有順序和沒有順序都可以,都不影響錢幣的最小個數。
所以本題并不強調集合是組合還是排列。
如果求組合數就是外層for循環遍歷物品,內層for遍歷背包。
如果求排列數就是外層for遍歷背包,內層for循環遍歷物品。
-
舉例推導dp數組,
以輸入:coins = [1, 2, 5], amount = 5為例
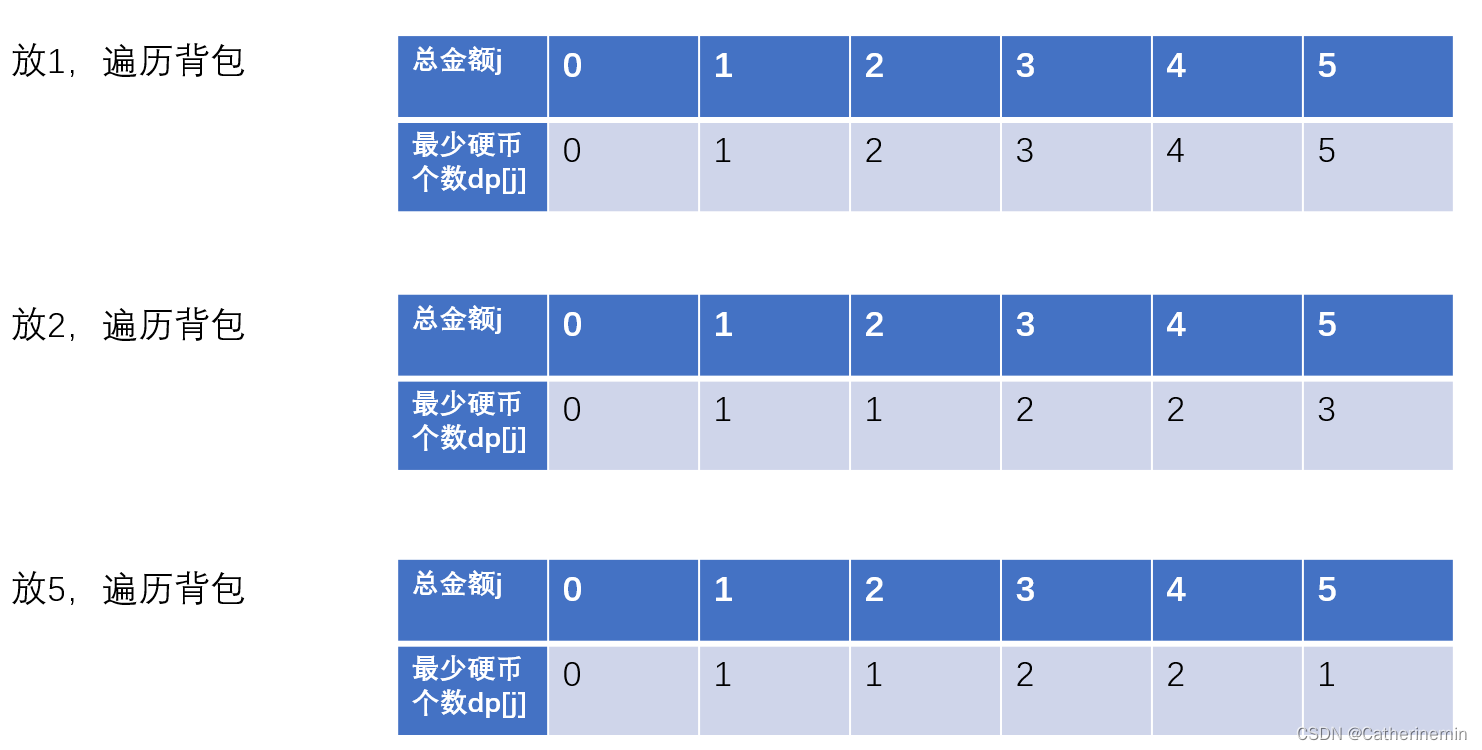
復雜度分析:
- 時間復雜度:
O(n * amount),n 為coins長度 - 空間復雜度:
O(amount)
class Solution {public int coinChange(int[] coins, int amount) {int max = Integer.MAX_VALUE;int[] dp = new int[amount + 1];//初始化dp數組為最大值for (int j = 0; j < dp.length; j++) {dp[j] = max;}//當金額為0時需要的硬幣數目為0dp[0] = 0;for (int i = 0; i < coins.length; i++) {//正序遍歷:完全背包每個硬幣可以選擇多次for (int j = coins[i]; j <= amount; j++) {//只有dp[j-coins[i]]不是初始最大值時,該位才有選擇的必要if (dp[j - coins[i]] != max) {//選擇硬幣數目最小的情況dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);}}}return dp[amount] == max ? -1 : dp[amount];}public static void main(String[] args) {Solution solution = new Solution();solution.coinChange(new int[] {1,2,5},5);}
}
從貪心的角度看,每次放最大的硬幣,一直放,直到amount剩下為amount%最大硬幣值,接著放次大或能直接整除的硬幣。
class Solution {public int coinChange(int[] coins, int amount) {if (amount == 0) return 0;if (coins.length == 1 && amount % coins[0] != 0) return -1;int count = 0;Arrays.sort(coins);for (int i = coins.length - 1; i >= 0; i--) {count += amount / coins[i];amount = amount % coins[i];if (amount == 0) {return count;}}return -1;}
}
但是這個代碼不能通過,貪心不能通過局部最優獲取全局最優。
279. 完全平方數
給你一個整數 n ,返回 和為 n 的完全平方數的最少數量 。
完全平方數 是一個整數,其值等于另一個整數的平方;換句話說,其值等于一個整數自乘的積。例如,1、4、9 和 16 都是完全平方數,而 3 和 11 不是。
示例 1:
輸入:n = 12
輸出:3
解釋:12 = 4 + 4 + 4
示例 2:
輸入:n = 13
輸出:2
解釋:13 = 4 + 9
提示:
1 <= n <= 104
教程:https://programmercarl.com/0279.%E5%AE%8C%E5%85%A8%E5%B9%B3%E6%96%B9%E6%95%B0.html#_279-%E5%AE%8C%E5%85%A8%E5%B9%B3%E6%96%B9%E6%95%B0
方法一:動態規劃
思路:完全平方數就是物品(可以無限件使用),湊個正整數n就是背包,問湊滿這個背包最少有多少物品?
完全背包
步驟
-
定義dp [j]:和為j的完全平方數的最少數量為dp[j]。
-
遞推公式:
dp[j] 可以由dp[j - i * i]推出, dp[j - i * i] + 1 便可以湊成dp[j]。
此時我們要選擇最小的dp[j],所以遞推公式:dp[j] = min(dp[j - i * i] + 1, dp[j]);
-
dp數組初始化:dp[0] =0,dp[j]賦最大值
-
確定遍歷順序:
兩者都可:
如果求組合數就是外層for循環遍歷物品,內層for遍歷背包。
如果求排列數就是外層for遍歷背包,內層for循環遍歷物品。
-
舉例推導dp數組,
已輸入n為5例,dp狀態圖如下:

復雜度分析:
- 時間復雜度:
O(n*sqrt(n)) - 空間復雜度:
O(n)
class Solution {// 版本一,先遍歷物品, 再遍歷背包public int numSquares(int n) {int max = Integer.MAX_VALUE;int[] dp = new int[n + 1];//初始化for (int j = 0; j <= n; j++) {dp[j] = max;}//如果不想要寫for-loop填充數組的話,也可以用JAVA內建的Arrays.fill()函數。//Arrays.fill(dp, Integer.MAX_VALUE);//當和為0時,組合的個數為0dp[0] = 0;// 遍歷物品for (int i = 1; i * i <= n; i++) {// 遍歷背包for (int j = i * i; j <= n; j++) {//if (dp[j - i * i] != max) {dp[j] = Math.min(dp[j], dp[j - i * i] + 1);//}//不需要這個if statement,因爲在完全平方數這一題不會有"湊不成"的狀況發生( 一定可以用"1"來組成任何一個n),故comment掉這個if statement。}}return dp[n];}
}class Solution {// 版本二, 先遍歷背包, 再遍歷物品public int numSquares(int n) {int max = Integer.MAX_VALUE;int[] dp = new int[n + 1];// 初始化for (int j = 0; j <= n; j++) {dp[j] = max;}// 當和為0時,組合的個數為0dp[0] = 0;// 遍歷背包for (int j = 1; j <= n; j++) {// 遍歷物品for (int i = 1; i * i <= j; i++) {dp[j] = Math.min(dp[j], dp[j - i * i] + 1);}}return dp[n];}
}
——推導式)


















