昨天一直在復盤梯度下降，都沒咋預習邏輯回歸，好在不是很難，來捋捋

邏輯回歸簡介

邏輯回歸是解決分類問題

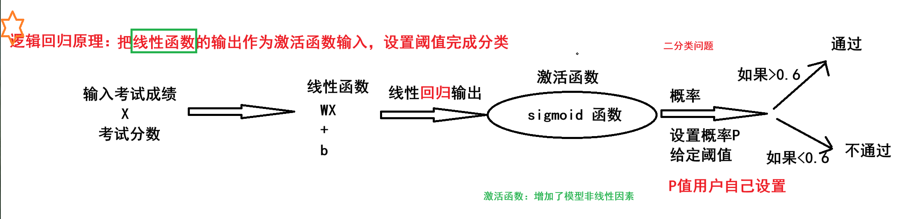
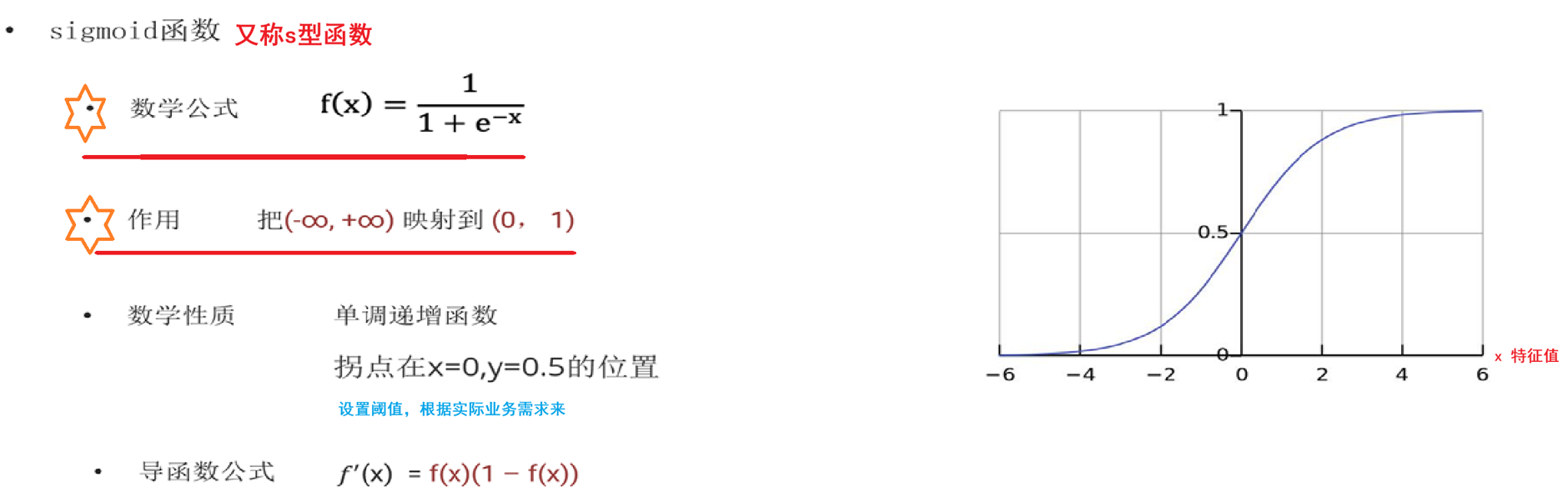
數學基礎-sigmoid函數

還要回顧一下概率論

極大似然估計

再來看一下對數

邏輯回歸原理

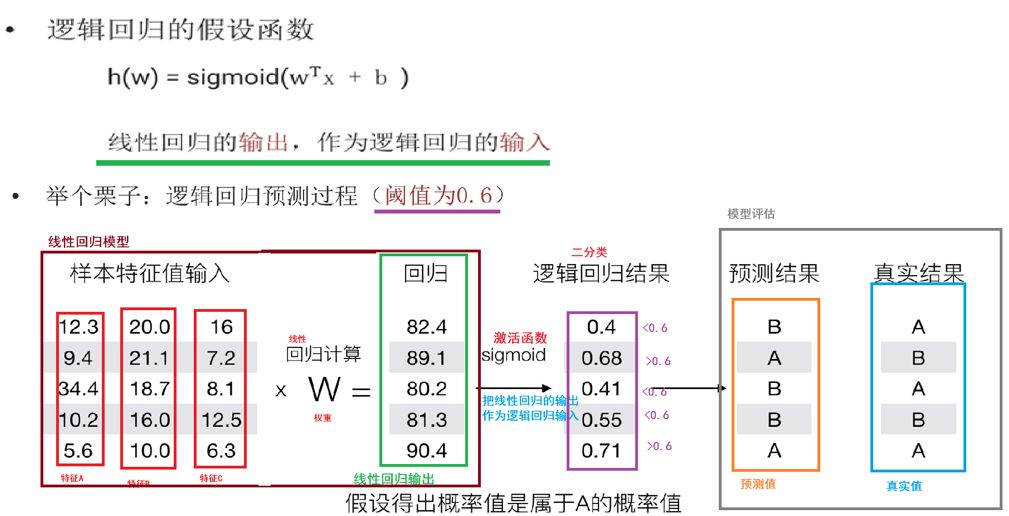
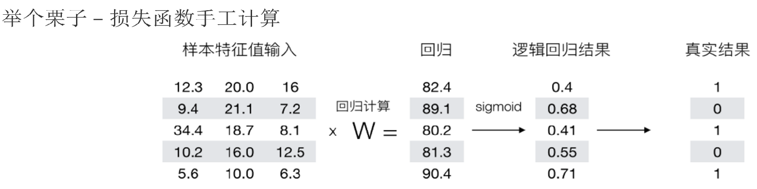
邏輯回歸的損失函數

例子：

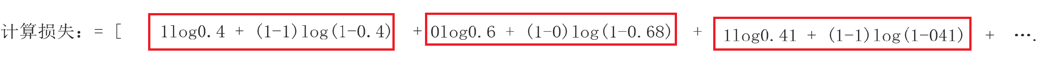
分類問題評估

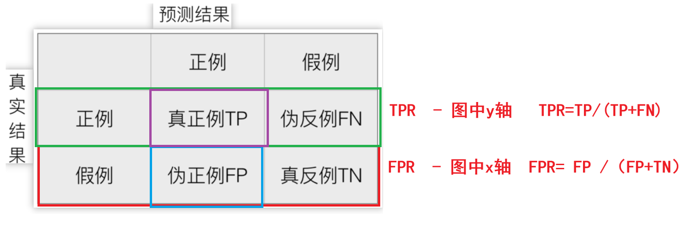
混淆矩陣（重點）

這個得記住，不難記，按英文名記就好了：

真實結果這邊兩個在預測的正例中就是Ture和False

在預測的反例就是倒過來False和Ture

預測的正例就是Positive，反例Negative

所以結合一下：

真正：Ture Positive（TP）? ? ? ? ? ?偽假：False Negative（FN）

偽正：False Positive（FP）? ? ? ? ?真假：Ture Negative（TN）

這樣去理解：

例子：

精確率（Precision）

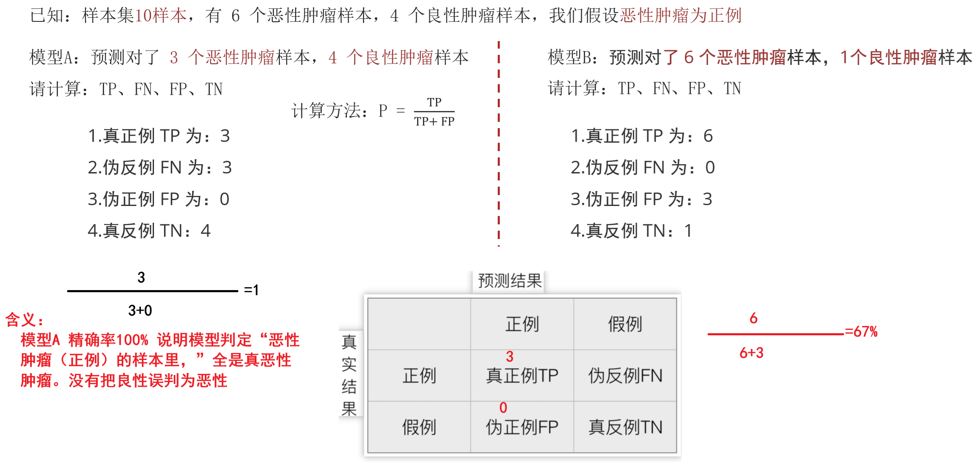
召回率（recall）

也叫查全率，指的是預測為真正例樣本占所有真實正例樣本的比重例如：惡性腫瘤當做正例樣本，則我們想知道模型是否能把所有的惡性腫瘤患者都預測出來。

計算方法：P = TP+?TP/(TP+ FN)

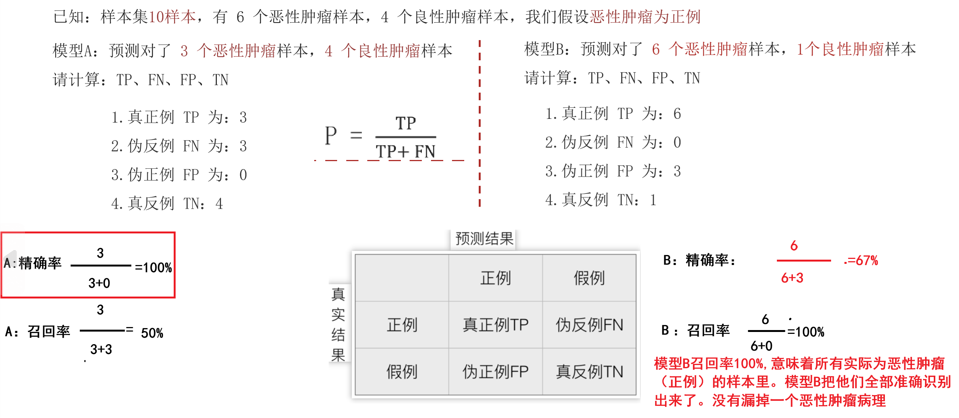
F1-score

ROC曲線、AUC指標

真正率TPR與假正率FPR

正樣本中被預測為正樣本的概率TPR （True Positive Rate）

負樣本中被預測為正樣本的概率FPR （False Positive Rate）

通過這兩個指標可以描述模型對正/負樣本的分辨能力

真正率TRP（True Positive Rate）

是作為ROC曲線的Y軸

假正率FPR（False Positive Rate）

作X軸

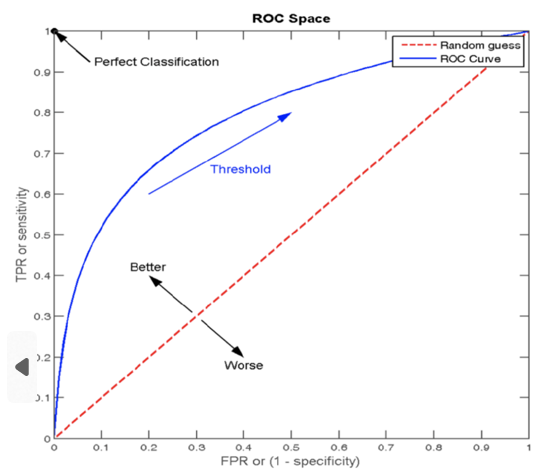
ROC曲線（Receiver Operating Characteristic curve）

是一種常用于評估分類模型性能的可視化工具。ROC曲線以模型的真正率TPR為縱軸，假正率FPR為橫軸，它將模型在不同閾值下的表現以曲線的形式展現出來

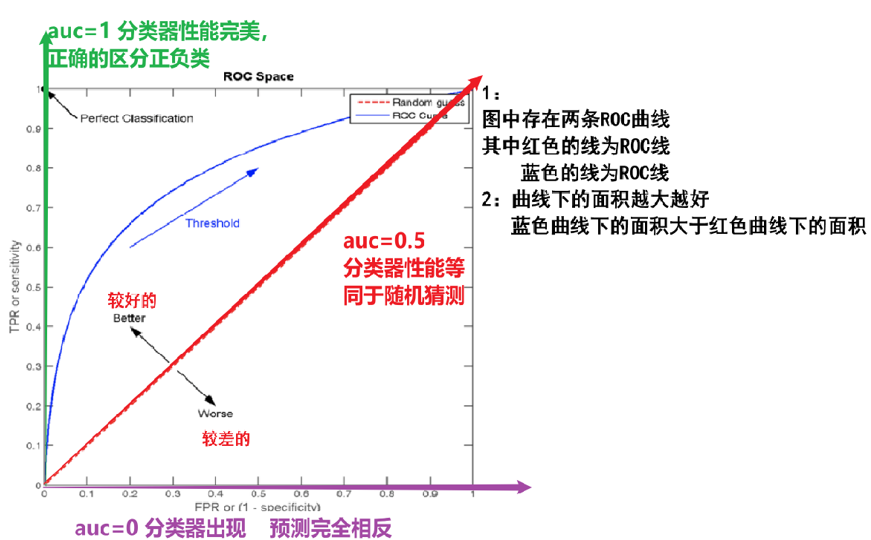
AUC (Area Under the ROC Curve）曲線下面積

ROC曲線的優劣可以通過曲線下的面積（AUC）來衡量，AUC越大表示分類器性能越好。

當AUC=0.5時，表示分類器的性能等同于隨機猜測

當AUC=1時，表示分類器的性能完美，能夠完全正確地將正負例分類。

圖像中四個特殊點（頂點）的意義要稍微記一下

import pandas as pd
from sklearn.metrics import confusion_matrix,precision_score,recall_score,f1_score, roc_curve, auc
import matplotlib.pyplot as plt
import numpy as np# 設置中文字體支持
plt.rcParams['font.sans-serif'] = ['SimHei', 'Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False#todo 1、定義數據集  真實樣本(10個  6個惡性  4個良性)   -》手動設置 惡性（正例） 良性（反例）
y_train=['惡性','惡性','惡性','惡性','惡性','惡性','良性','良性','良性','良性']#todo 2、 定義標簽名
label=['惡性','良性']  #標簽1：正樣本（正例）  標簽2:負樣本（反例）
df_label=['惡性（正例）','良性（假例）']  #這是為了讓格式好看#todo 3、定義 預測結果A   3個惡性 ，4個良性   改完后數據集  3個惡性   7個良性
y_pre_A=['惡性','惡性','惡性',     '良性','良性','良性',    '良性','良性','良性','良性']#todo 4、 把上述的預測結果A 轉換為 混淆矩陣
cm_A=confusion_matrix(y_train,y_pre_A,labels=label)
# print(f"混淆矩陣A：\n{cm_A}")  #美化#todo 5、把混淆矩陣 轉化為 DataFrame格式
df_A=pd.DataFrame(cm_A,index=df_label,columns=df_label)
print(f"預處結果A對應的DataFrame對象:\n{df_A}")#todo 6、 定義 預測結果B 預測對了 -》 6個惡性  1個良性
y_pre_B=['惡性','惡性','惡性','惡性','惡性','惡性','良性','惡性','惡性','惡性']
cm_B=confusion_matrix(y_train,y_pre_B,labels=label)
df_B =pd.DataFrame(cm_B,index=df_label,columns=df_label)
print(f"預處結果B對應的DataFrame對象:\n{df_B}")#總結： 混淆矩陣已經開發完成，接下來，計算他的TP\FN\FP\TN#todo 7 打印預測結果
#精確率  參1： 真實樣本  參2：預測樣本   參3：正例標簽
print(f"預測結果A的精確率：{precision_score(y_train,y_pre_A,pos_label='惡性')}")
print(f"預測結果B的精確率：{precision_score(y_train,y_pre_B,pos_label='惡性')}")#召回率
print(f"預測結果A的召回率:{recall_score(y_train,y_pre_A,pos_label='惡性')}")
print(f"預測結果B的召回率:{recall_score(y_train,y_pre_B,pos_label='惡性')}")#F1值
print(f"預測結果A的F1值:{f1_score(y_train,y_pre_A,pos_label='惡性')}")
print(f"預測結果B的F1值:{f1_score(y_train,y_pre_B,pos_label='惡性')}")# 繪制ROC曲線
# 首先需要將標簽轉換為數字
y_train_num = [1 if label == '惡性' else 0 for label in y_train]
y_pre_A_num = [1 if label == '惡性' else 0 for label in y_pre_A]
y_pre_B_num = [1 if label == '惡性' else 0 for label in y_pre_B]# 為了獲得更平滑的ROC曲線，我們需要生成預測概率而不是硬分類
# 這里我們模擬概率值來演示平滑的ROC曲線
np.random.seed(42)  # 為了結果可重現
y_pre_A_proba = []
for label in y_pre_A:if label == '惡性':# 對于預測為惡性的，我們生成一個相對高的惡性概率y_pre_A_proba.append(np.random.uniform(0.6, 1.0))else:# 對于預測為良性的，我們生成一個相對低的惡性概率y_pre_A_proba.append(np.random.uniform(0.0, 0.4))y_pre_B_proba = []
for label in y_pre_B:if label == '惡性':# 對于預測為惡性的，我們生成一個相對高的惡性概率y_pre_B_proba.append(np.random.uniform(0.7, 1.0))else:# 對于預測為良性的，我們生成一個相對低的惡性概率y_pre_B_proba.append(np.random.uniform(0.0, 0.3))# 計算ROC曲線
fpr_A, tpr_A, _ = roc_curve(y_train_num, y_pre_A_proba)
fpr_B, tpr_B, _ = roc_curve(y_train_num, y_pre_B_proba)# 計算AUC值
auc_A = auc(fpr_A, tpr_A)
auc_B = auc(fpr_B, tpr_B)# 繪制ROC曲線
plt.figure(figsize=(8, 6))
plt.plot(fpr_A, tpr_A, color='blue', lw=2, label=f'預測結果A (AUC = {auc_A:.2f})')
plt.plot(fpr_B, tpr_B, color='red', lw=2, label=f'預測結果B (AUC = {auc_B:.2f})')
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--', label='隨機猜測')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('假正率 (False Positive Rate)')
plt.ylabel('真正率 (True Positive Rate)')
plt.title('ROC曲線對比')
plt.legend(loc="lower right")
plt.grid(True)
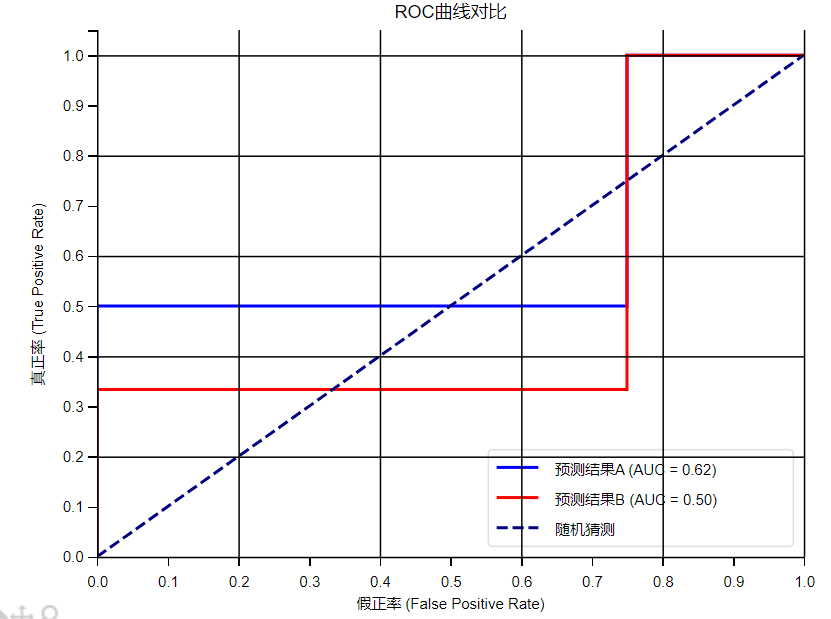
plt.show()

由于這個案例是將結果分成了幾個類，而不是計算概率，所以曲線圖變成了折線圖，不過大家理解這個意思就好