題目描述

給你二叉樹的根結點 root ，請你將它展開為一個單鏈表：

展開后的單鏈表應該同樣使用 TreeNode ，其中 right 子指針指向鏈表中下一個結點，而左子指針始終為 null 。
展開后的單鏈表應該與二叉樹 先序遍歷 順序相同。

示例 1：

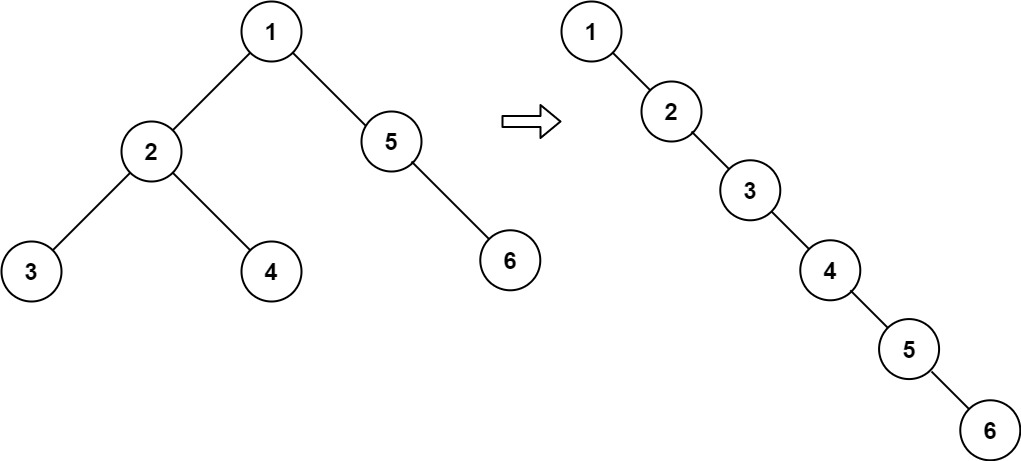
輸入：root = [1,2,5,3,4,null,6]
輸出：[1,null,2,null,3,null,4,null,5,null,6]

示例 2：
輸入：root = []
輸出：[]

示例 3：
輸入：root = [0]
輸出：[0]

提示：
樹中結點數在范圍 [0, 2000] 內
-100 <= Node.val <= 100

進階：你可以使用原地算法（O(1) 額外空間）展開這棵樹嗎？

思考：前序遍歷+左子樹鏈表化

核心是遞歸處理左右子樹：先將左、右子樹分別展開為鏈表，再將左子樹鏈表接到根節點的右指針，最后將原右子樹鏈表接到左子樹鏈表的尾部，實現“根→左子樹鏈表→右子樹鏈表”的前序順序。

算法過程

1. 遞歸終止條件：若當前節點為null（空樹/葉子節點的子樹），返回null（無需處理）。
2. 遞歸展開子樹：
   • 遞歸展開左子樹，得到左子樹鏈表的頭節點left；
   • 遞歸展開右子樹，得到右子樹鏈表的頭節點right。
3. 重組當前節點的指針：
   • 將當前節點的右指針指向左子樹鏈表（root.right = left），左指針置為null（root.left = null）；
   • 遍歷左子樹鏈表至尾部（找到最后一個節點），將其右指針指向右子樹鏈表（current.right = right）。
4. 返回當前節點：作為上層節點的左/右子樹鏈表頭，完成遞歸回溯。

時空復雜度

• 時間復雜度：O(n)，n為二叉樹節點總數。
  原因：每個節點僅被訪問1次（遞歸處理），遍歷左子樹鏈表尾部的操作總次數為O(n)（每個節點最多被遍歷1次），總時間與節點數線性相關。
• 空間復雜度：O(h)，h為二叉樹高度。
  原因：遞歸調用棧深度取決于樹高，平衡樹h=O(log n)，鏈狀樹h=O(n)；額外空間僅為遞歸棧，無其他存儲開銷。

代碼（前序遍歷版）

/*** Definition for a binary tree node.* function TreeNode(val, left, right) {*     this.val = (val===undefined ? 0 : val)*     this.left = (left===undefined ? null : left)*     this.right = (right===undefined ? null : right)* }*/
/*** @param {TreeNode} root* @return {void} Do not return anything, modify root in-place instead.*/
var flatten = function(root) {preOrder(root);
};// 輔助函數：將以root為根的樹展開為鏈表，返回展開后的頭節點
function preOrder(root) {if (!root) return null; // 空節點直接返回// 遞歸展開左、右子樹let left = preOrder(root.left);let right = preOrder(root.right);// 1. 將左子樹鏈表接到根節點的右指針，左指針置空root.right = left;root.left = null;// 2. 找到左子樹鏈表的尾部，將右子樹鏈表接在其后let current = root;while (current.right) { // 遍歷至左子樹鏈表的最后一個節點current = current.right;}current.right = right;return root; // 返回當前節點作為上層的子樹鏈表頭
}

關鍵邏輯解析

1. 為何用前序遍歷？
   題目要求展開后的鏈表順序與前序遍歷一致（根→左→右），前序遍歷的遞歸順序天然匹配這一需求：先處理根節點，再處理左子樹，最后處理右子樹，確保重組后的指針順序正確。

2. 左指針為何必須置空？
   展開后的鏈表要求所有節點的左指針為null，僅保留右指針指向后續節點。若不置空左指針，會導致鏈表中殘留左子樹引用，破壞“鏈表”的結構定義。

3. 如何高效找到左子樹鏈表的尾部？
   代碼中通過while (current.right)循環遍歷左子樹鏈表至尾部，這是最直觀的實現。對于極端情況（左子樹為鏈狀），該操作時間復雜度為O(k)（k為左子樹節點數），但整棵樹的總遍歷次數仍為O(n)（每個節點最多被遍歷1次），不影響整體時間復雜度。

4. 是否可以優化空間復雜度？
   上述遞歸實現的空間復雜度為O(h)，若需進一步優化至O(1)，可采用Morris遍歷（線索化遍歷），通過修改空指針臨時指向前驅/后繼節點，避免遞歸棧開銷，但代碼邏輯會更復雜。

示例解析（以 root = [1,2,5,3,4,null,6] 為例）

1. 遞歸展開左子樹（2→3→4）和右子樹（5→6）；
2. 根節點1的右指針指向左子樹2，左指針置空；
3. 遍歷左子樹鏈表至尾部（4），將其右指針指向右子樹5；
4. 最終鏈表為：1→2→3→4→5→6，符合前序遍歷順序。

該過程通過遞歸自然實現了“根→左→右”的順序重組，確保鏈表結構正確且原地修改（不創建新節點）。