在訓練模型時我們可能會遇到模型不滿足于預期需要進行改善的環節,這些情況通常包括以下幾種常見問題和對應的解決方案:
數據質量不足
- 數據量過少:當訓練樣本不足時,模型難以學習到有效的特征表示。建議通過數據增強(如圖像旋轉、加噪等)或收集更多數據來解決
- 數據不平衡:某些類別樣本遠多于其他類別時,可以采用過采樣(如SMOTE)、欠采樣或類別加權等方法
- 數據質量問題:需要檢查并處理缺失值、異常值和標注錯誤
模型欠擬合
- 表現為訓練集和驗證集上表現都不佳
- 可能原因:模型結構過于簡單、特征工程不足或正則化過度
- 解決方案:增加模型復雜度、優化特征選擇、減少正則化強度模型過擬合
模型過擬合
- 表現為訓練集表現很好但驗證集表現差
- 可能原因:模型過于復雜、訓練數據不足或訓練輪次過多
- 解決方案:增加dropout層、使用早停(early stopping)、添加L1/L2正則化、數據增強
一、數據集改善
1、數據集拆分
1. 核心功能??
train_test_split是 scikit-learn 中用于將數據集隨機劃分為訓練集和測試集的函數,主要作用包括:
??防止過擬合??:通過分離訓練和測試數據,評估模型在未見數據上的泛化能力。
??靈活劃分比例??:支持自定義測試集或訓練集的比例(如 80% 訓練 + 20% 測試)。
??分層抽樣??:處理類別不均衡數據時,保持訓練集和測試集的類別分布一致。
??2. 參數詳解??
??參數?? | ??說明?? | ??示例值?? |
|---|---|---|
| 待劃分的數據(如特征? |
|
| 測試集比例(0.0-1.0)或樣本數。默認 0.25 。 |
|
| 訓練集比例,若未設置則自動補全? |
|
| 隨機種子,保證劃分結果可復現 。 |
|
| 是否打亂數據(默認? |
|
| 按標簽分層抽樣,保持類別比例一致 。 |
|
3.示例
from sklearn.model_selection import train_test_split
import numpy as npX = np.array([[1, 2], [3, 4], [5, 6], [7, 8]])
y = np.array([0, 1, 0, 1])# 80% 訓練集,20% 測試集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
print("訓練集:", X_train) # 輸出示例:[[3 4], [1 2], [7 8]]
print("測試集:", X_test) # 輸出示例:[[5 6]][1,5]2.樣本歸一化
樣本歸一化是指對數據集中的??每個樣本(行)??進行縮放,使其滿足特定范數(如L1、L2或最大值范數),從而消除樣本間量綱差異。與特征歸一化(按列處理)不同,樣本歸一化適用于樣本向量需整體比較的場景,如文本分類、聚類分析等。
??1.核心公式??
??L2歸一化(默認)??:
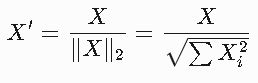
使每個樣本的歐幾里得范數為1。
??L1歸一化??:
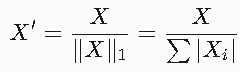
使樣本的絕對值和為1。
??最大值歸一化(Max)??:
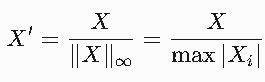
將樣本最大值縮放到1。
??2. 適用場景??
??文本數據處理??
如TF-IDF向量或詞頻向量,歸一化后可比性更強。??基于距離的算法??
KNN、SVM等需計算樣本間距離的模型,歸一化避免大數值特征主導結果。??神經網絡輸入??
歸一化到統一范圍(如[0,1])可加速梯度下降收斂。??圖像處理??
像素值歸一化后更適應卷積神經網絡的輸入要求。
??3. 方法對比與選擇??
??方法?? | ??特點?? | ??適用場景?? |
|---|---|---|
??L2歸一化?? | 保留樣本向量的方向信息,對異常值敏感度較低 | 文本分類、聚類分析 |
??L1歸一化?? | 生成稀疏解,適合特征選擇 | 高維稀疏數據(如詞袋模型) |
??Max歸一化?? | 快速縮放至[-1,1],但對極端值敏感 | 圖像像素值處理 |
??注意事項??:
若樣本中存在異常值,建議使用L2歸一化或RobustScaler(基于中位數和四分位數)。
歸一化會改變原始數據分布,但保留相對大小關系
?代碼實現(Python)
使用Scikit-learn的Normalizer?
from sklearn.preprocessing import Normalizer
import numpy as np# 示例數據(每行一個樣本)
X = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])# L2歸一化(默認)
normalizer = Normalizer(norm='l2')
X_l2 = normalizer.fit_transform(X)
print("L2歸一化結果:\n", X_l2)#[0.267, 0.534, 0.801]# L1歸一化
normalizer = Normalizer(norm='l1')
X_l1 = normalizer.fit_transform(X)
print("L1歸一化結果:\n", X_l1)?3.樣本標準化
樣本標準化(也稱為數據標準化或特征縮放)是將不同尺度的數據轉換為統一尺度的過程,使不同特征具有可比性。
常見的標準化方法
??Z-score標準化(標準差標準化)??
公式:z = (x - μ) / σ
其中μ是均值,σ是標準差
處理后數據均值為0,標準差為1
??Min-Max標準化??
公式:x' = (x - min) / (max - min)
將數據線性變換到[0,1]區間
??Max標準化??
公式:x' = x / max
將數據按最大值縮放
??小數縮放??
公式:x' = x / 10^j
j為使最大絕對值小于1的最小整數
標準化的作用
消除不同特征間的量綱影響
提高模型收斂速度(特別是梯度下降算法)
提高模型精度
使不同特征對模型有相近的貢獻度
應用場景
基于距離的算法(如KNN、K-means)
使用梯度下降的模型(如神經網絡)
主成分分析(PCA)等降維方法
正則化模型(如Lasso、Ridge回歸)
Z-score標準化
import numpy as np
from sklearn.preprocessing import StandardScaler# 原始數據
data = np.array([[1, 2], [3, 4], [5, 6]])# 使用sklearn
scaler = StandardScaler()
scaled_data = scaler.fit_transform(data)
print("Z-score標準化結果:\n", scaled_data)# 手動計算
mean = np.mean(data, axis=0)
std = np.std(data, axis=0)
manual_scaled = (data - mean) / std
print("手動計算結果:\n", manual_scaled)?Min-Max標準化
from sklearn.preprocessing import MinMaxScaler# 使用sklearn
minmax_scaler = MinMaxScaler()
minmax_scaled = minmax_scaler.fit_transform(data)
print("Min-Max標準化結果:\n", minmax_scaled)# 手動計算
data_min = np.min(data, axis=0)
data_max = np.max(data, axis=0)
manual_minmax = (data - data_min) / (data_max - data_min)
print("手動計算結果:\n", manual_minmax)4.上采樣和下采樣
上采樣和下采樣是處理數據不平衡問題的兩種常用技術,主要用于解決分類任務中類別分布不均的情況。
下采樣(Downsampling)
基本概念
也稱為欠采樣(Undersampling)
減少多數類樣本數量,使其與少數類樣本數量接近或相同
適用于多數類樣本數量遠大于少數類的情況
常用方法
??隨機下采樣??
從多數類中隨機刪除樣本
from sklearn.utils import resample# 假設df是DataFrame,'class'是目標列 majority_class = df[df['class'] == 0] minority_class = df[df['class'] == 1]# 隨機下采樣多數類 majority_downsampled = resample(majority_class,replace=False,n_samples=len(minority_class),random_state=42)# 合并下采樣后的數據 df_downsampled = pd.concat([majority_downsampled, minority_class])??Tomek Links??
移除邊界附近造成分類困難的多數類樣本
from imblearn.under_sampling import TomekLinkstl = TomekLinks() X_res, y_res = tl.fit_resample(X, y)??Cluster Centroids??
使用聚類方法減少多數類樣本
from imblearn.under_sampling import ClusterCentroidscc = ClusterCentroids(random_state=42)
X_res, y_res = cc.fit_resample(X, y)優缺點
??優點??:
減少訓練數據量,加快訓練速度
解決類別不平衡問題
??缺點??:
可能丟失重要信息
可能導致模型欠擬合
上采樣(Upsampling)
基本概念
也稱為過采樣(Oversampling)
增加少數類樣本數量,使其與多數類樣本數量接近或相同
適用于少數類樣本數量不足的情況
常用方法
??隨機上采樣??
隨機復制少數類樣本
from sklearn.utils import resampleminority_upsampled = resample(minority_class,replace=True,n_samples=len(majority_class),random_state=42)df_upsampled = pd.concat([majority_class, minority_upsampled])
??SMOTE(Synthetic Minority Oversampling Technique)??
合成新的少數類樣本
from imblearn.over_sampling import SMOTEsmote = SMOTE(random_state=42)
X_res, y_res = smote.fit_resample(X, y)??ADASYN(Adaptive Synthetic Sampling)??
基于數據分布的自適應上采樣
from imblearn.over_sampling import ADASYNadasyn = ADASYN(random_state=42)
X_res, y_res = adasyn.fit_resample(X, y)優缺點
??優點??:
不丟失原始信息
可以改善模型對少數類的識別能力
??缺點??:
可能導致過擬合
增加計算負擔
二、交叉驗證
交叉驗證是評估機器學習模型性能和選擇超參數的重要技術,它通過將數據集分成多個子集來減少評估結果的方差。
常見交叉驗證方法
1. K折交叉驗證(K-Fold CV)
??原理??:將數據集隨機分成K個大小相似的互斥子集(稱為"折"),每次用K-1折訓練,剩下1折驗證,重復K次。
from sklearn.model_selection import KFold, cross_val_score
from sklearn.linear_model import LogisticRegressionkfold = KFold(n_splits=5, shuffle=True, random_state=42)
model = LogisticRegression()
scores = cross_val_score(model, X, y, cv=kfold)
print("平均準確率:", scores.mean())2. 分層K折交叉驗證(Stratified K-Fold)
??特點??:保持每個折中類別比例與原始數據集一致,適用于分類問題,特別是類別不平衡時。
from sklearn.model_selection import StratifiedKFoldskf = StratifiedKFold(n_splits=5, shuffle=True, random_state=42)
scores = cross_val_score(model, X, y, cv=skf)3. 留一法交叉驗證(Leave-One-Out, LOO)
??原理??:每次留一個樣本作為驗證集,其余作為訓練集,重復N次(N為樣本數)。
from sklearn.model_selection import LeaveOneOutloo = LeaveOneOut()
scores = cross_val_score(model, X, y, cv=loo)
print("LOO平均準確率:", scores.mean())4. 留P法交叉驗證(Leave-P-Out)
??原理??:每次留P個樣本作為驗證集。
from sklearn.model_selection import LeavePOutlpo = LeavePOut(p=2)
scores = cross_val_score(model, X, y, cv=lpo) # 注意:計算量很大5. 時間序列交叉驗證(Time Series CV)
??特點??:考慮數據的時間順序,防止未來信息泄露。
from sklearn.model_selection import TimeSeriesSplittscv = TimeSeriesSplit(n_splits=5)
for train_index, test_index in tscv.split(X):X_train, X_test = X[train_index], X[test_index]y_train, y_test = y[train_index], y[test_index]交叉驗證的最佳實踐
??數據預處理??:應在交叉驗證循環內進行,防止數據泄露
from sklearn.pipeline import make_pipeline from sklearn.preprocessing import StandardScalerpipeline = make_pipeline(StandardScaler(), LogisticRegression()) scores = cross_val_score(pipeline, X, y, cv=5)??類別不平衡處理??:使用分層抽樣或自定義采樣策略
from sklearn.model_selection import StratifiedKFoldskf = StratifiedKFold(n_splits=5)??隨機性控制??:設置
random_state確保結果可復現??折數選擇??:
小數據集:5-10折
大數據集:3-5折(減少計算量)
超參數調優:可使用更多折數
??性能指標選擇??:根據問題類型選擇合適的評估指標
from sklearn.metrics import make_scorer, f1_scorescorer = make_scorer(f1_score, average='macro') scores = cross_val_score(model, X, y, cv=5, scoring=scorer)
交叉驗證的局限性
計算成本高,特別是大數據集或復雜模型
對數據順序敏感的數據集(如時間序列)需要特殊處理
極端不平衡數據可能需要分層抽樣或其他采樣技術
交叉驗證是機器學習工作流中不可或缺的部分,合理使用可以有效評估模型泛化能力并防止過擬合。
三、數據結果
混淆矩陣
混淆矩陣是評估分類模型性能的重要工具,它以矩陣形式直觀展示模型的預測結果與真實標簽的對比情況。
基本結構
對于二分類問題,混淆矩陣為2×2矩陣:
??TP(True Positive)??:真正例,實際為陽性且預測為陽性
??FN(False Negative)??:假反例,實際為陽性但預測為陰性
??FP(False Positive)??:假正例,實際為陰性但預測為陽性
??TN(True Negative)??:真反例,實際為陰性且預測為陰性
#Python實現
from sklearn.metrics import confusion_matrix
import matplotlib.pyplot as plt
import seaborn as sns# 示例數據
y_true = [1, 0, 1, 1, 0, 1, 0, 0]
y_pred = [1, 0, 0, 1, 0, 1, 1, 0]# 計算混淆矩陣
cm = confusion_matrix(y_true, y_pred)
print("混淆矩陣:\n", cm)# 可視化
plt.figure(figsize=(6, 6))
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues', xticklabels=['預測陰性', '預測陽性'],yticklabels=['真實陰性', '真實陽性'])
plt.xlabel('預測值')
plt.ylabel('真實值')
plt.title('混淆矩陣')
plt.show()分類指標
指標 | 公式 | 側重 | 適用場景 | sklearn函數 |
|---|---|---|---|---|
準確率 | (TP+TN)/Total | 整體正確率 | 平衡數據集 | accuracy_score |
精確率 | TP/(TP+FP) | 預測陽性準確度 | FP代價高 | precision_score |
召回率 | TP/(TP+FN) | 陽性樣本識別率 | FN代價高 | recall_score |
F1分數 | 2(PR)/(P+R) | 精確率召回率平衡 | 不平衡數據 | f1_score |
AUC | ROC曲線下面積 | 整體區分能力 | 閾值無關評估 | roc_auc_score |









-什么是以太幣)









