本文為GESP 2023年9月 六級的上機題目詳細題解和講解視頻，覺得有幫助或者寫的不錯可以點個贊。

題目一講解視頻

題目二講解視頻

題目一:小羊買飲料

B3873 [GESP202309 六級] 小楊買飲料 - 洛谷

題目大意:

現在超市一共有n種飲料，每種飲料有對應的售價c元，和容量l毫升。

現在你每種飲料只能買一瓶，并且最后要買至少L毫升飲料。

請問在這個前提下，最少花多少錢。

解題思路:

很明顯的背包dp。

我們回顧一下原始的01背包問題：

有n個物品，每個物品都有價值v,和重量w，背包容量是C，我們需要在小于等于C的背包容量下獲取最大的價值。

這個題目呢，可以理解成，n個物品，每個物品都有價值c和容量i，我們必須要使得最終背包的容量大于等于L，并且讓價值盡可能少！

經過上述分析，很明顯就能想到以下的思路：

我們令dp[i][v]表示用前i個飲料，恰好湊到v升飲料的最小花費

我們最多可以達到tot = sum(l1,l2,l3,...ln)升飲料

那么對于第i個飲料，可以不

dp[i][j] = dp[i - 1][j]

或者買

令val = 第i個飲料的價值，c = 第i個飲料的容量

dp[i][j] = dp[i - 1][j - val] + c

使得價值最低，也就是

dp[i][j] = min(dp[i][j], dp[i - 1][j - val] + c)

然后呢，最終算的結果是對于前N個飲料，容量大于等于L的時候的最小價值。

也就是我們遍歷j從L 到 mx，計算dp[N][j]的最小值。這個方法即使寫成一維數組也會超內存，因為tot 的最大值為5e8。

我們需要優化一下。

我們可以注意到，只要是大于等于L的部分，都可以理解成是等于L的。

那么也就是我們dp數組實際大小只需要開到L + 1就可以了，實際計算的時候把大于L的部分算成L即可。

實際實現可以是，在遍歷的時候，設置一個當前j可達的一個容量cur,cur = min(L, j + val)

如果dp[i - 1][j]可以達到，那么dp[i][cur] = min(dp[i][cur], dp[i - 1][j] + cost)

代碼(C++):

#include <bits/stdc++.h>using i64 = long long;int main() {std::ios::sync_with_stdio(false);std::cin.tie(nullptr);int n, L;std::cin >> n >> L;std::vector<int> c(n), l(n);for (int i = 0; i < n; i++) {std::cin >> c[i] >> l[i];}int inf = INT_MAX;std::vector dp(n + 1, std::vector<int> (L + 1, inf));dp[0][0] = 0;for (int i = 1; i <= n; i++) {//整層拷貝,表示不選dp[i] = dp[i - 1];int cost = c[i - 1], val = l[i - 1];for (int j = 0; j <= L; j++) {int cur = std::min(L, j + val);if (dp[i - 1][j] != inf) {dp[i][cur] = std::min(dp[i][cur], dp[i - 1][j] + cost);}}}int ans = dp[n][L];std::cout << (ans == inf ? "no solution" : std::to_string(ans));
}

題目二:小楊的握手問題

B3874 [GESP202309 六級] 小楊的握手問題 - 洛谷

題目大意:

現在有n個學生，編號為0到n -1，現在讓這n個學生按照某個順序進入教室。

當一個同學進入教室后，他需要和所有學號小于他的進行握手。

當所有同學按照某個順序進入教室后，請問總共的握手次數是多少？

解題思路一:歸并排序

這個題目可以抽象為，求一個數組中順序對的個數。

為了方便，我們這里就求逆序對的數量cnt，然后用總對數減去cnt即為答案

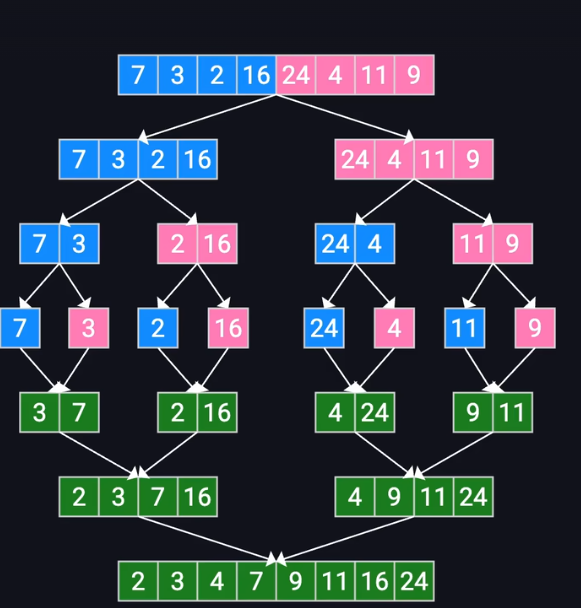
下面是歸并排序的原理圖，每次把當前的數組分成一半，然后分到最后的時候進行合并。

我們可以在合并的過程中求逆序對數目，比如說合并7 3，是逆序的，逆序對數目加一

合并2 3 7 16和4 9 11 24，4是小于7的，那么4肯定小于7之后所有的數字。

代碼一(C++):

#include <bits/stdc++.h>using i64 = long long;i64 mSort(std::vector<int>& a, std::vector<int>& tmp, int l, int r) {if (r - l <= 1) {return 0;}i64 cnt = 0;int m = (l + r) / 2;cnt += mSort(a, tmp, l, m);cnt += mSort(a, tmp, m, r);int i = l, j = m, k = l;while (i < m && j < r) {if (a[i] <= a[j]) {tmp[k] = a[i];k++;i++;} else {tmp[k] = a[j];cnt += m - i;j++;k++;}}while (i < m) {tmp[k] = a[i];i++;k++;}while (j < r) {tmp[k] = a[j];j++;k++;}for (int i = l; i < r; i++) {a[i] = tmp[i];}return cnt;
}int main() {std::ios::sync_with_stdio(false);std::cin.tie(nullptr);int n;std::cin >> n;std::vector<int> a(n);for (int i = 0; i < n; i++) {std::cin >> a[i];}std::vector<int> tmp(n);i64 tot = 1LL * n * (n - 1) / 2;i64 cnt = mSort(a, tmp, 0, n);std::cout << tot - cnt << "\n";
}

解題思路二:樹狀數組

我們可以這么理解題目，現在有一個長度為n的數組t, 并且剛開始都為0。

我們可以持續的進行下面這個過程求順序對個數：

現在編號為x同學進入教室

我們可以把t[x]設置成1，并且看x前面有多少個1，前面的肯定是比當前x小的，也就是求前面部分的前綴和！

那么問題抽象成了，每次把x增加1，然后求[0, x - 1]的前綴和。可以用樹狀數組加速處理！

代碼二(C++):

#include <bits/stdc++.h>using i64 = long long;// 模板來源：https://leetcode.cn/circle/discuss/mOr1u6/
// FenwickTree 模板（1-indexed）
template<typename T>
class FenwickTree {std::vector<T> tree;public:// 使用下標 1 到 nFenwickTree(int n) : tree(n + 1) {}// a[i] 增加 val, i 為 1-indexed// 時間復雜度 O(log n)void update(int i, T val) {for (; i < tree.size(); i += i & -i) {tree[i] += val;}}// 求前綴和 a[1] + ... + a[i]// 時間復雜度 O(log n)T pre(int i) const {T res = 0;for (; i > 0; i &= i - 1) {res += tree[i];}return res;}// 求區間和 a[l] + ... + a[r]T query(int l, int r) const {if (r < l) return 0;return pre(r) - pre(l - 1);}
};int main() {std::ios::sync_with_stdio(false);std::cin.tie(nullptr);int n;std::cin >> n;FenwickTree<int> ft(n);i64 ans = 0;for (int i = 0; i < n; i++) {int id;std::cin >> id;id += 1;ans += ft.pre(id);ft.update(id, 1);}std::cout << ans << "\n";
}