102. 二叉樹的層序遍歷

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public List<List<Integer>> levelOrder(TreeNode root) {// 創建結果列表，用于存儲每層的節點值List<List<Integer>> ret = new ArrayList<List<Integer>>();// 處理空樹情況if (root == null) {return ret;}// 創建隊列用于BFS遍歷，初始時加入根節點Queue<TreeNode> queue = new LinkedList<TreeNode>();queue.offer(root);  // 將根節點加入隊列// 開始BFS遍歷while (!queue.isEmpty()) {// 創建當前層的節點值列表List<Integer> level = new ArrayList<Integer>();// 記錄當前層的節點數量int currentLevelSize = queue.size();// 遍歷當前層的所有節點for (int i = 1; i <= currentLevelSize; ++i) {// 從隊列頭部取出一個節點TreeNode node = queue.poll();// 將節點值加入當前層列表level.add(node.val);// 將該節點的子節點加入隊列（先左后右）if (node.left != null) {queue.offer(node.left);}if (node.right != null) {queue.offer(node.right);}}// 將當前層的節點值列表加入結果列表ret.add(level);}// 返回層序遍歷結果return ret;}
}

關鍵點說明

1. BFS（廣度優先搜索）算法：

   • 使用隊列數據結構實現

   • 從根節點開始，按層級依次遍歷

2. 層序遍歷的特點：

   • 每層節點單獨存儲在一個子列表中

   • 結果是一個二維列表，每個子列表代表一層的節點值

3. 隊列的使用：

   • offer()方法用于將元素加入隊列尾部

   • poll()方法用于從隊列頭部取出元素

4. 時間復雜度：

   • O(n)：每個節點被訪問一次

   • n為二叉樹中的節點總數

5. 空間復雜度：

   • O(n)：最壞情況下隊列需要存儲所有葉子節點

示例執行流程

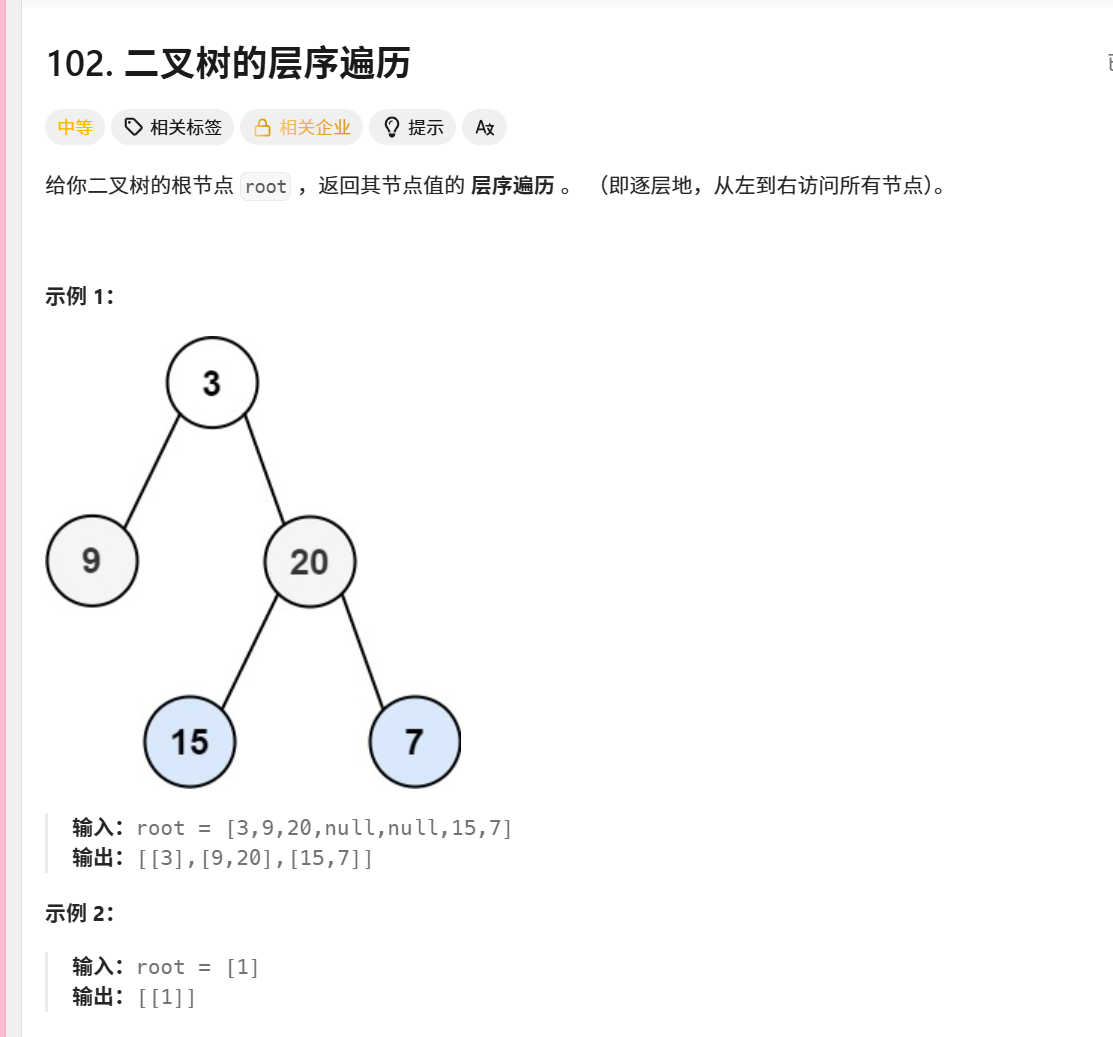
對于如下二叉樹：

text

    3/ \9  20/  \15   7

執行過程：

1. 初始隊列：[3]

   • 處理3，加入子列表[3]

   • 加入子節點9,20 → 隊列：[9,20]

2. 處理隊列：[9,20]

   • 處理9 → 子列表[9]（無子節點）

   • 處理20 → 子列表[9,20]

   • 加入子節點15,7 → 隊列：[15,7]

3. 處理隊列：[15,7]

   • 處理15 → 子列表[15]（無子節點）

   • 處理7 → 子列表[15,7]（無子節點）

4. 最終結果：[[3], [9,20], [15,7]]

108. 將有序數組轉換為二叉搜索樹

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public TreeNode sortedArrayToBST(int[] nums) {return helper(nums, 0, nums.length - 1);}public TreeNode helper(int[] nums,int left, int right){if(left>right){return null;}int tip=(left+right)/2;TreeNode root = new TreeNode(nums[tip]);root.left=helper(nums, left, tip-1);root.right=helper(nums,tip+1,right);return root;}
}

/**
?* Definition for a binary tree node.
?* public class TreeNode {
?* ? ? int val;
?* ? ? TreeNode left;
?* ? ? TreeNode right;
?* ? ? TreeNode() {}
?* ? ? TreeNode(int val) { this.val = val; }
?* ? ? TreeNode(int val, TreeNode left, TreeNode right) {
?* ? ? ? ? this.val = val;
?* ? ? ? ? this.left = left;
?* ? ? ? ? this.right = right;
?* ? ? }
?* }
?*/
class Solution {
? ? /**
? ? ?* 將有序數組轉換為高度平衡的二叉搜索樹
? ? ?* @param nums 有序整數數組
? ? ?* @return 二叉搜索樹的根節點
? ? ?*/
? ? public TreeNode sortedArrayToBST(int[] nums) {
? ? ? ? // 調用輔助函數，傳入數組和初始邊界
? ? ? ? return helper(nums, 0, nums.length - 1);
? ? }
? ??
? ? /**
? ? ?* 遞歸輔助函數，構建BST
? ? ?* @param nums 有序數組
? ? ?* @param left 當前子數組的左邊界
? ? ?* @param right 當前子數組的右邊界
? ? ?* @return 構建好的子樹根節點
? ? ?*/
? ? public TreeNode helper(int[] nums, int left, int right) {
? ? ? ? // 遞歸終止條件：左邊界超過右邊界
? ? ? ? if (left > right) {
? ? ? ? ? ? return null;
? ? ? ? }
? ? ? ??
? ? ? ? // 選擇中間位置作為當前子樹的根節點
? ? ? ? // 這樣能保證樹的高度平衡
? ? ? ? int mid = (left + right) / 2;
? ? ? ??
? ? ? ? // 創建當前根節點
? ? ? ? TreeNode root = new TreeNode(nums[mid]);
? ? ? ??
? ? ? ? // 遞歸構建左子樹（使用左半部分數組）
? ? ? ? root.left = helper(nums, left, mid - 1);
? ? ? ??
? ? ? ? // 遞歸構建右子樹（使用右半部分數組）
? ? ? ? root.right = helper(nums, mid + 1, right);
? ? ? ??
? ? ? ? return root;
? ? }
}

關鍵點說明

1. 高度平衡BST的定義：

   • 每個節點的左右子樹高度差不超過1

   • 通過總是選擇中間元素作為根節點來保證平衡性

2. 分治算法思想：

   • 將問題分解為更小的子問題（左子樹和右子樹）

   • 合并子問題的解（構建當前樹）

3. 時間復雜度：

   • O(n)：每個元素只被訪問一次

   • n為數組長度

4. 空間復雜度：

   • O(log n)：遞歸棧的深度

   • 對于平衡BST，樹的高度為log n

5. 中間位置選擇：

   • mid = (left + right) / 2?對于偶數長度數組，可以選擇中間偏左或偏右

   • 這里選擇的是偏左的位置（因為整數除法會截斷小數）

示例執行流程

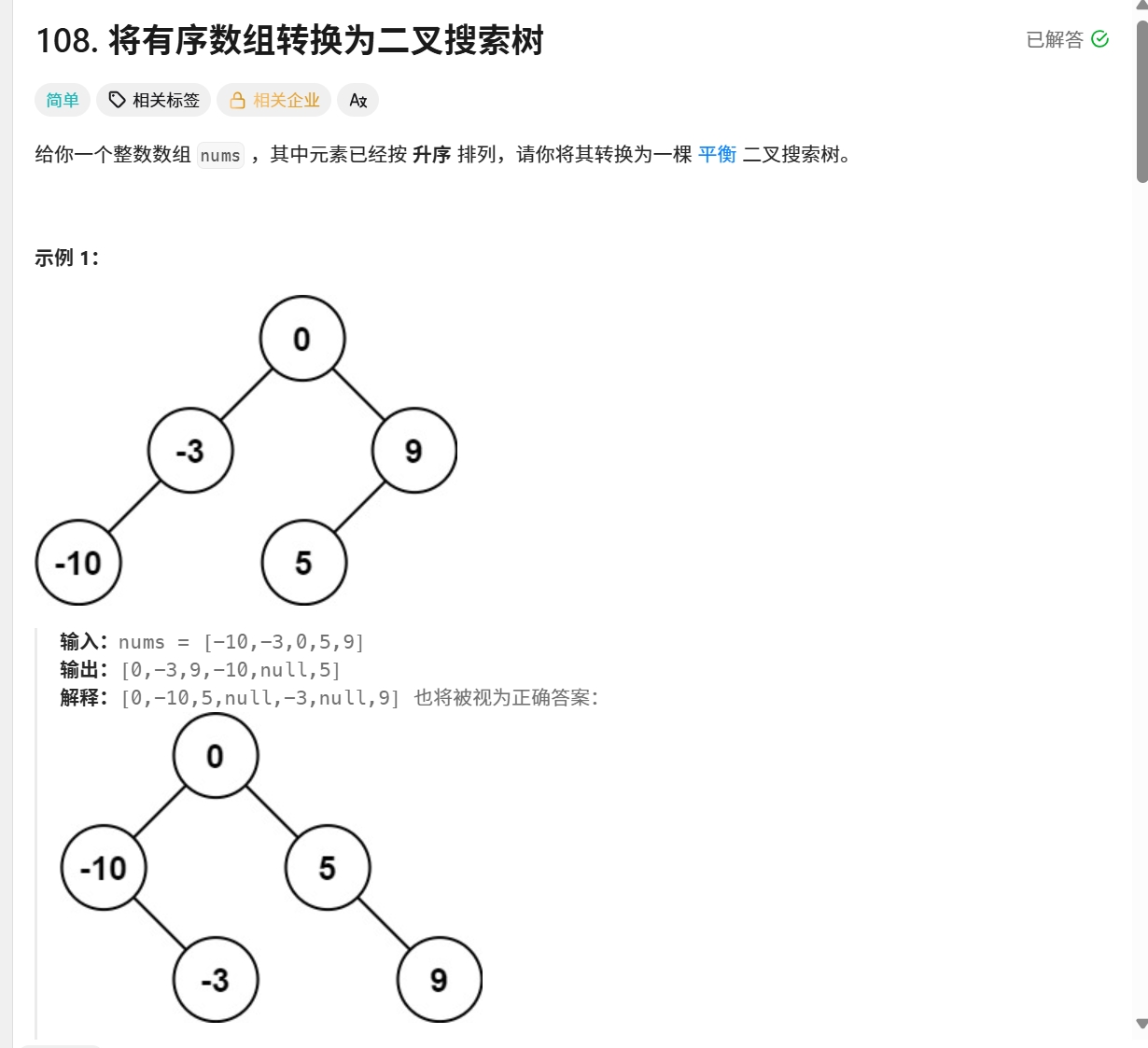
對于輸入數組：[-10, -3, 0, 5, 9]

構建過程：

1. 初始調用：helper(nums, 0, 4)

   • mid=2 → root=0

   • 左子樹：helper(nums, 0, 1)

     • mid=0 → root=-10

     • 左子樹：helper(nums, 0, -1) → null

     • 右子樹：helper(nums, 1, 1)

       • mid=1 → root=-3

       • 左右子樹均為null

   • 右子樹：helper(nums, 3, 4)

     • mid=3 → root=5

     • 左子樹：helper(nums, 3, 2) → null

     • 右子樹：helper(nums, 4, 4)

       • mid=4 → root=9

       • 左右子樹均為null

最終BST結構：

text

      0/ \-10  5\   \-3   9

算法變體

1. 選擇中間偏右的位置：

   java

   int mid = (left + right + 1) / 2;

   對于偶數長度數組會選擇中間偏右的元素

2. 迭代實現：
   可以使用棧來模擬遞歸過程，避免遞歸調用

3. 處理大數據集：
   對于非常大的數組，可以考慮將數組分段處理

這種實現方式充分利用了有序數組和二叉搜索樹的特性，通過分治策略高效地構建出平衡的二叉搜索樹。