Heterophily-Aware Representation Learning on Heterogeneous Graphs （TPAMI 2025） 計算機科學 1區 I:18.6 top期刊

?? 摘要

現實世界中的圖結構通常非常復雜，不僅具有全局結構上的異質性，還表現出局部鄰域內的強異質相似性（heterophily）。雖然越來越多的研究揭示了圖神經網絡（GNN）在處理同質圖中異質相似性時的局限性，但在異質圖中研究異質相似性的工作仍然非常有限。

為填補這一研究空白，本文基于元路徑（metapaths）對異質圖中的異質相似性進行了定義，并提出了兩個實用的度量指標來定量描述異質相似性的程度。通過對真實異質圖的實證分析，作者發現現有的異質圖神經網絡（HGNN）——通常繼承自同質圖中的GNN機制——在面對具有異質相似性或低同質性的異質圖時難以泛化。

為應對這一挑戰，作者提出了一種新方法 HETERO2NET，該模型是一種面向異質圖中異質相似性的HGNN。它結合了 遮蔽元路徑預測（masked metapath prediction） 和 遮蔽標簽預測（masked label prediction） 兩項任務，能夠靈活高效地處理同質性和異質性共存的圖結構。

在五個具有不同異質相似性水平的真實世界異質圖上進行的實驗表明，HETERO2NET 在半監督節點分類任務中表現優異，超過了多種強大基線方法。特別是，該模型還能擴展至具有1300萬節點和1.57億邊的工業級商業圖，展示出處理大規模復雜異質圖的能力。

Index Terms—Heterogeneous Graphs, Heterogeneous Graph Neural Networks, Homophily and Heterophily

1 引言

圖結構在現實世界的應用中變得日益普遍，因為它們能夠建模各種領域中復雜的關系和互聯結構。借助這一趨勢，圖神經網絡（GNN） 迅速發展，成為分析圖結構數據的強大工具，并在眾多圖學習任務中達到了最先進的性能 [1]–[4]。近年來，研究人員開始積極探索 GNN 在處理異質圖（heterogeneous graphs）方面的潛力。異質圖也被稱為異構信息網絡（heterogeneous information networks），它們的特點是由多種類型的節點和邊構成，每個節點或邊代表不同類型的實體或關系。這種節點和邊類型的多樣性給異質圖中的語義挖掘帶來了巨大挑戰——不僅要理解每種節點的語義，還要解析不同類型節點之間豐富而復雜的關系。

為應對異質性的挑戰，研究者提出了大量異質圖神經網絡（HGNNs），用于解決與異質圖相關的任務，如異質節點分類、鏈接預測和推薦系統等 [8], [9]。HGNN 是 GNN 在異質圖場景下的擴展，能夠聯合學習圖的結構信息和語義信息。HGNN 的研究大致可分為兩類：

• 一類方法通過 定義并利用元路徑（meta-paths） 來建模異質結構 [5], [8], [10], [11]；
• 另一類方法則屬于 無元路徑范式（metapath-free paradigms），這類方法像傳統 GNN 一樣從節點的局部鄰域中聚合信息，但引入額外的模塊將節點類型和邊類型等語義信息嵌入到消息傳播過程中 [6], [7], [12]–[14]。

盡管 GNN 和 HGNN 已取得了顯著成功，越來越多的研究文獻 [15], [15]–[20] 也揭示了一個重要的局限性：常規 GNN 在處理異質相似性（heterophily）較強的圖時表現較差，特別是在同質圖中，當相連節點擁有不同的標簽和/或屬性時（即“異性相吸”原則）。雖然現有的 HGNN 在設計上繼承了許多原本為同質圖開發的 GNN 機制，但目前尚不清楚 HGNN 是否能夠有效處理具有異質相似性的異質圖——這一問題在現有文獻中尚未被明確定義和深入研究。

為彌補這一研究空白，本文旨在通過引入基于元路徑（metapaths）的異質圖中異質相似性（heterophily）定義，為該方向建立一個新的研究基礎。元路徑本身是異質圖中一個定義良好的概念 [5], [8]。
如圖 1 所示，作者指出異質圖學習中面臨的三大核心挑戰：

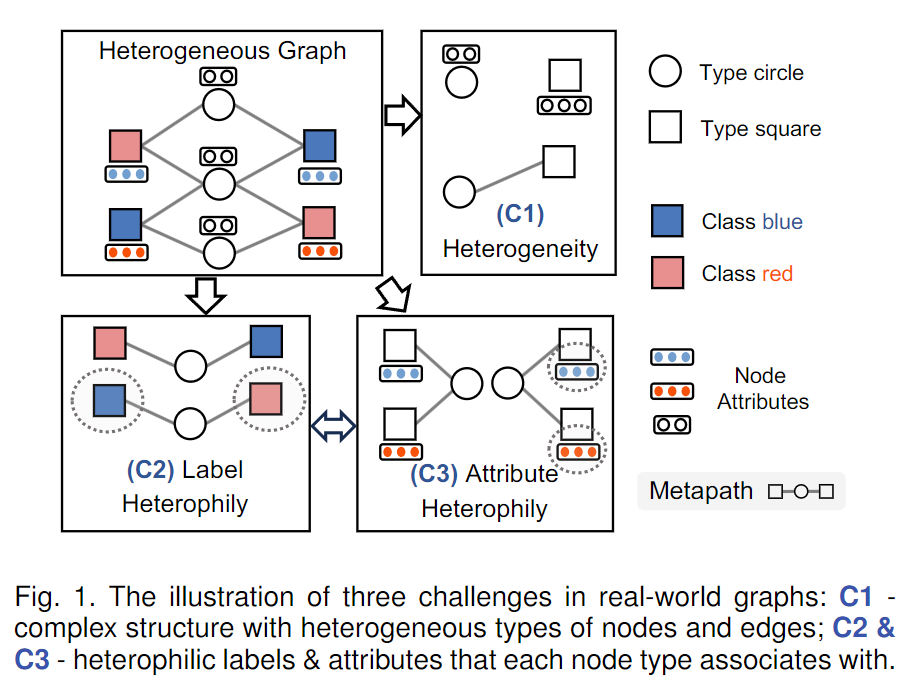
1. 圖的異質性（heterogeneity），
2. 標簽異質相似性（label heterophily），
3. 屬性異質相似性（attribute heterophily）。

在這里，異質相似性指的是：兩個相同類型的節點通過元路徑相連，但它們在標簽或屬性上存在差異。

為了量化異質相似性的程度，作者提出了兩個實用的度量指標：

• 基于元路徑的標簽同質性（MLH）：將傳統的同質性比率 [16] 從同質圖擴展到了異質圖；
• 基于元路徑的 Dirichlet 能量（MDE）：衡量局部鄰域中特征的平滑性。

通過實證研究，作者發現：在 MLH 和 MDE 指標下，當前的 HGNN 模型在異質圖中難以泛化到異質相似性較強（或同質性較低/中等）的場景。在這類場景下，甚至一些完全不利用圖結構的模型（如多層感知機 MLP）在許多情況下都優于 HGNN，這一發現進一步凸顯了現有方法的局限性。

針對上述挑戰，本文提出了一種新穎的異質圖神經網絡模型 HETERO2NET，它具備異質相似性感知能力，能夠同時應對在標簽或屬性層面具有 同質性（homophily）或異質性（heterophily） 的異質圖。在技術上，HETERO2NET 引入了 遮蔽元路徑預測（masked metapath prediction） 機制，分別學習解耦的同質性與異質性表示。這兩類表示能夠捕捉圖中不同的屬性信號，從而有助于下游任務的執行。此外，HETERO2NET 還引入了 遮蔽標簽預測（masked label prediction） 策略，以增強節點之間的消息傳播，特別是對于那些表現出強標簽異質性的節點。這兩種設計分別有助于解決屬性異質性和標簽異質性帶來的挑戰。

我們的主要貢獻如下：

• 異質相似性度量與現有方法的局限性：我們提出了兩個基于元路徑的異質相似性度量指標 —— MLH（標簽同質性） 和 MDE（屬性Dirichlet能量），分別用于衡量異質圖中的標簽異質性和屬性異質性。通過實證研究，我們揭示了現有 HGNN 在處理具有異質相似性的異質圖時的顯著局限性，而這一問題在現有文獻中長期被忽視，其根本原因是缺乏明確的異質性度量方法。

• 面向異質相似性的全新模型：基于上述挑戰，我們提出了 HETERO2NET —— 一個新穎的、具有異質相似性感知能力的 HGNN。該模型通過引入解耦的遮蔽圖預測任務和遮蔽標簽預測任務，能夠靈活高效地處理同質性與異質性共存的異質圖（其技術細節如圖 2 所示）。

• 大規模實證驗證：我們在五個真實世界的異質圖數據集上進行了實驗評估，包括一個包含 1300 萬節點和 1.57 億邊的工業級商業圖。實驗結果表明，HETERO2NET 在半監督節點分類任務中表現優越，在性能和可擴展性方面均優于多種強基線方法。

論文結構安排：

本文其余部分的結構安排如下：

• 第 2 部分 回顧了與本研究相關的已有工作；
• 第 3 部分 介紹了基本符號和必要的預備知識；
• 第 4 部分 提出了兩個基于元路徑的異質相似性度量指標，并進行了關于不同異質性水平異質圖的實證研究；
• 第 5 部分 詳細介紹了我們提出的 HETERO2NET 框架，包括解耦的遮蔽元路徑預測和遮蔽標簽預測兩項關鍵技術；
• 第 6 部分 展示了實驗結果；
• 最后，第 7 部分 總結了全文，并展望了異質圖學習在更廣泛場景中的未來研究方向。

2 相關工作

本節回顧與本研究密切相關的文獻，主要包括以下兩個方面的研究進展：

• 異質圖神經網絡（Heterogeneous Graph Neural Networks, HGNNs）；
• 在異質相似性圖上進行的圖表示學習（Graph Representation Learning over Heterophilic Graphs）。

2.1 異質圖神經網絡（Heterogeneous Graph Neural Networks, HGNNs）

近年來，為了滿足對高效建模各種異質圖日益增長的需求，出現了大量關于 HGNN 的研究工作 [24]。
根據處理圖中語義信息的方式不同，HGNN 大致可以分為兩類：基于元路徑的方法 和 非元路徑的方法。

• 基于元路徑的 HGNN 通過手工設計或自動選擇的元路徑進行鄰居特征的傳播與聚合。
  例如：
  • Metapath2Vec [8] 使用元路徑引導的隨機游走，捕捉異質節點之間的語義信息；
  • GTN [25] 為不同元路徑分配可學習的權重，從而自動學習有用的元路徑；
  • HAN [5] 引入層次注意力機制，分別建模節點層級和語義層級的結構；
  • 作為后續工作，MAGNN [11] 在 HAN 的基礎上引入了元路徑聚合機制，以從多個元路徑中學習語義信息。

非元路徑的 HGNN 方法將傳統 GNN 中的消息傳遞與聚合機制擴展到異質圖上，無需手動設計有意義的元路徑。

例如：

• RGCN [12] 及其后續工作 RGAT [26] 提出針對每種邊類型提取關系特定的模式，然后將不同語義信息進行融合；
• SHGN [7] 引入了多層圖注意力網絡，并在邊注意力機制中加入可學習的邊類型嵌入；
• HGSL [27] 通過挖掘復雜交互關系，聯合學習異質圖結構和 GNN 參數；
• 受到 Transformer [28] 成功經驗的啟發，HGT [6] 和 HINormer [22] 將自注意力機制引入圖結構的消息傳遞中，用于建模異質節點之間的結構依賴關系。

2.2 異質相似性圖上的學習

異質相似性圖（heterophilic graphs）是指：相連節點更可能具有不同的屬性或標簽。近年來，這一類圖結構受到了研究界越來越多的關注 [15], [15]–[20]。異質相似性問題為圖分析與建模帶來了獨特挑戰。

• Pei 等人 [16] 首次關注到這一現象，并提出了一種度量圖的同質性水平的指標；
• Zhu 等人 [15] 隨后深入研究了 GNN 在異質或非同質圖上性能下降的問題，并提出了 H2GCN，以在存在異質相似性的情況下改進圖結構的學習；
• CPGNN [17] 通過引入兼容性矩陣（compatibility matrix），將 GNN 泛化為同時支持同質性與異質性的圖；
• FAGCN [18] 在消息傳遞過程中引入了一種自適應整合機制，可動態融合低頻與高頻信號；
• LINKX [15] 關注如何將 GNN 擴展到大規模異質圖，通過 MLP 學習和融合特征矩陣與鄰接矩陣的信息；
• Luan 等人 [23] 從后聚合節點相似性的角度分析異質性，并提出了一種多通道混合機制，以提取豐富的本地信息，適應不同形式的節點異質相似性。

然而，大多數現有研究仍集中于同質圖，對于異質圖中的異質相似性問題尚缺乏深入探索。隨著異質圖在各類應用中的日益普及，開發能夠有效處理異質相似性并應對其帶來挑戰的方法變得愈發重要。近期也有一些并行工作的研究開始關注在異質相似性環境下進行異質圖學習 [30]–[33]。然而，這些方法普遍缺乏系統性的異質性量化指標，也缺少一個合理的框架來區分基于屬性的異質性與基于標簽的異質性，這正是促使我們開展本研究的動因。

3 預備知識（PRELIMINARY）

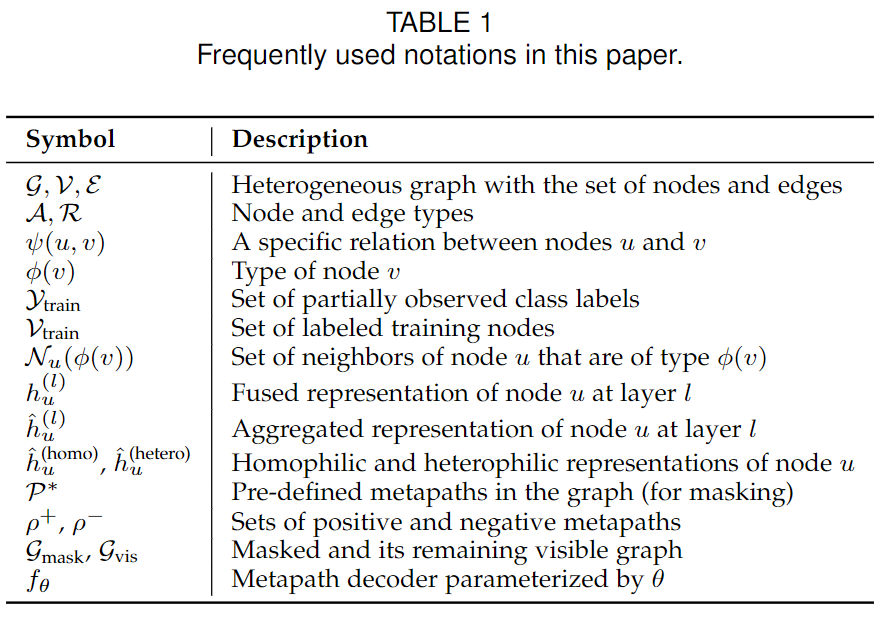
在本節中，我們將介紹與異質圖相關的基本概念和符號表示，同時引入用于衡量圖的同質性/異質性的度量指標。論文中經常使用的符號已在表 1中進行了匯總。

3.1 異質圖（Heterogeneous Graphs）

一個異質圖或稱為異構信息網絡，定義為：G={ V,E,A,R,φ,ψ}G = \{V, E, A, R, \varphi, \psi\}G={ V,E,A,R,φ,ψ} 其中，$V$ 和 $E$ 分別表示節點集合和邊集合。

該圖還包括：

• 一個節點類型映射函數 $\phi :V\to A$，用于將每個節點映射為其對應的類型；
• 一個邊類型映射函數 $\psi :E\to R$，用于將每條邊映射為其對應的關系類型（邊類型）；
• 其中，$A$ 表示所有可能的節點類型集合，$R$ 表示所有可能的關系類型集合，并且滿足 $|A|+|R|>2$。當 $|A|=|R|=1$ 時，圖 $G$ 就退化為一個同質圖。

在大多數情況下，圖 $G$ 是具備屬性的，即每個節點 $u\in V$ 都關聯一個 $d$-維的屬性向量 $x_u\in {\mathbb{R}}^d$。
在節點分類任務中，某些節點類型或特定的節點還會被分配一個類別標簽 $y$。然而，在異質圖中：

• 并非所有節點類型都具備標簽；
• 即使是帶標簽的節點類型，其內部通常也只有部分節點擁有標注信息。

3.2 異質圖中的元路徑（Metapath）

元路徑（Metapath）：
長度為 $n$ 的元路徑記作：$P?A_1\stackrel{R_1}{\to }{A}_2\stackrel{R_2}{\to }?\stackrel{R_n}{\to }{A}_{n+1}$

簡記為 $A_1{A}_2?A_{n+1}$，其中：

• $A_i\in A$ 表示節點類型，
• <