ss激活函數的作用是在隱藏層引入非線性，使得神經網絡能夠學習和表示復雜的函數關系，使網絡具備非線性能力，增強其表達能力。

一、常見激活函數

1、sigmoid

激活函數的作用是在隱藏層引入非線性，使得神經網絡能夠學習和表示復雜的函數關系，使網絡具備非線性能力，增強其表達能力。

（1）公式：

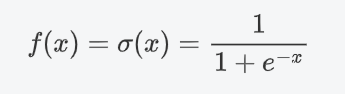
（2）特征

1. 將任意實數輸入映射到 (0, 1)之間，因此非常適合處理概率場景。

2. sigmoid函數一般只用于二分類的輸出層。

3. 微分性質: 導數計算比較方便，可以用自身表達式來表示：

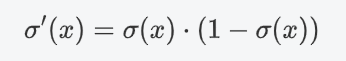
（3）缺點

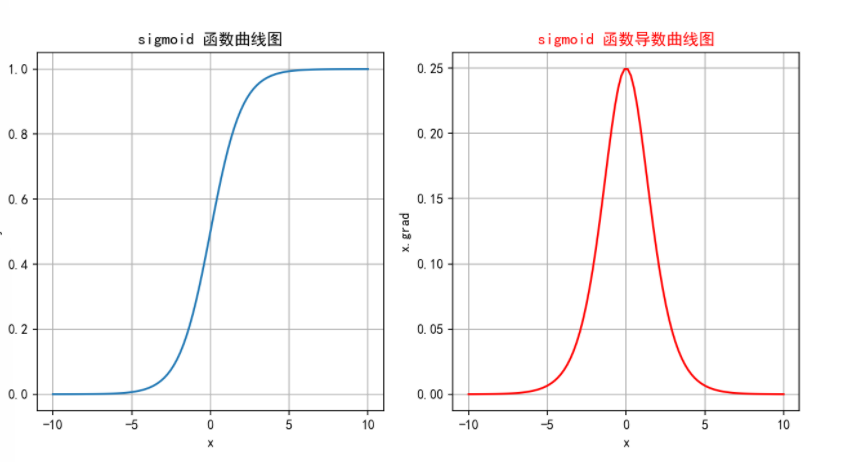
• 梯度消失:

  • 在輸入非常大或非常小時，Sigmoid函數的梯度會變得非常小，接近于0。這導致在反向傳播過程中，梯度逐漸衰減。

  • 最終使得早期層的權重更新非常緩慢，進而導致訓練速度變慢甚至停滯。

• 信息丟失：輸入100和輸入10000經過sigmoid的激活值幾乎都是等于 1 的，但是輸入的數據卻相差 100 倍。

• 計算成本高: 由于涉及指數運算，Sigmoid的計算比ReLU等函數更復雜，盡管差異并不顯著。

2、tanh

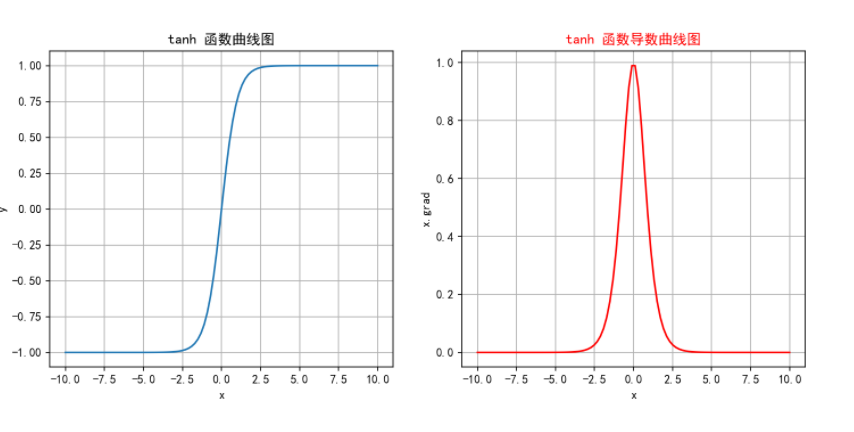
tanh(雙曲正切)是一種常見的非線性激活函數，常用于神經網絡的隱藏層。tanh 函數也是一種S形曲線，輸出范圍為(?1,1)。

（1）公式：

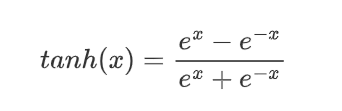
（2）特征

1. 輸出范圍: 將輸入映射到$$(-1, 1)$$之間，因此輸出是零中心的。相比于Sigmoid函數，這種零中心化的輸出有助于加速收斂。

2. 對稱性: Tanh函數關于原點對稱，因此在輸入為0時，輸出也為0。這種對稱性有助于在訓練神經網絡時使數據更平衡。

3. 平滑性: Tanh函數在整個輸入范圍內都是連續且可微的，這使其非常適合于使用梯度下降法進行優化。

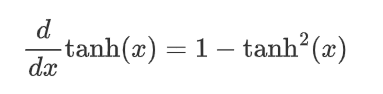
（3）缺點

1. 梯度消失: 雖然一定程度上改善了梯度消失問題，但在輸入值非常大或非常小時導數還是非常小，這在深層網絡中仍然是個問題。

2. 計算成本: 由于涉及指數運算，Tanh的計算成本還是略高，盡管差異不大。

3、ReLU

ReLU（Rectified Linear Unit）是深度學習中最常用的激活函數之一，它的全稱是修正線性單元。ReLU 激活函數的定義非常簡單，但在實踐中效果非常好。

（1）公式

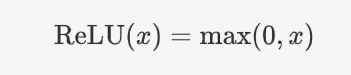
即ReLU對輸入x進行非線性變換：

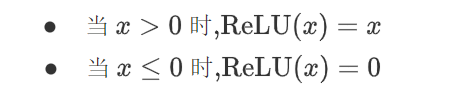
（2）特征

1. 計算簡單：ReLU 的計算非常簡單，只需要對輸入進行一次比較運算，這在實際應用中大大加速了神經網絡的訓練。

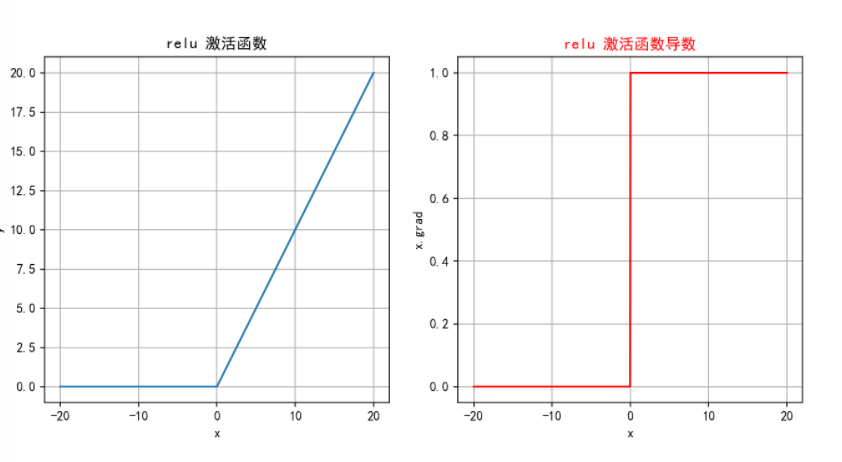
2. ReLU 函數的導數是分段函數：

   

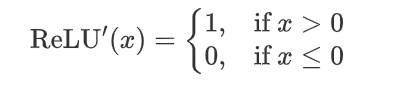
3. 緩解梯度消失問題：相比于 Sigmoid 和 Tanh 激活函數，ReLU 在正半區的導數恒為 1，這使得深度神經網絡在訓練過程中可以更好地傳播梯度，不存在飽和問題。

4. 稀疏激活：ReLU在輸入小于等于 0 時輸出為 0，這使得 ReLU 可以在神經網絡中引入稀疏性（即一些神經元不被激活），這種稀疏性可以提升網絡的泛化能力。

（3）缺點

神經元死亡：由于ReLU在x≤0時輸出為0，如果某個神經元輸入值是負，那么該神經元將永遠不再激活，成為“死亡”神經元。隨著訓練的進行，網絡中可能會出現大量死亡神經元，從而會降低模型的表達能力。

4、LeakyReLU

Leaky ReLU是一種對 ReLU 函數的改進，旨在解決 ReLU 的一些缺點，特別是神經元死亡的問題。Leaky ReLU 通過在輸入為負時引入一個小的負斜率來改善這一問題。

（1）公式

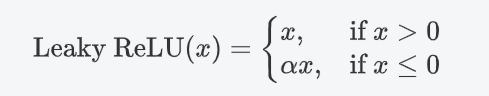
其中，alpha?是一個非常小的常數（如 0.01），它控制負半軸的斜率。這個常數 alpha是一個超參數，可以在訓練過程中可自行進行調整。

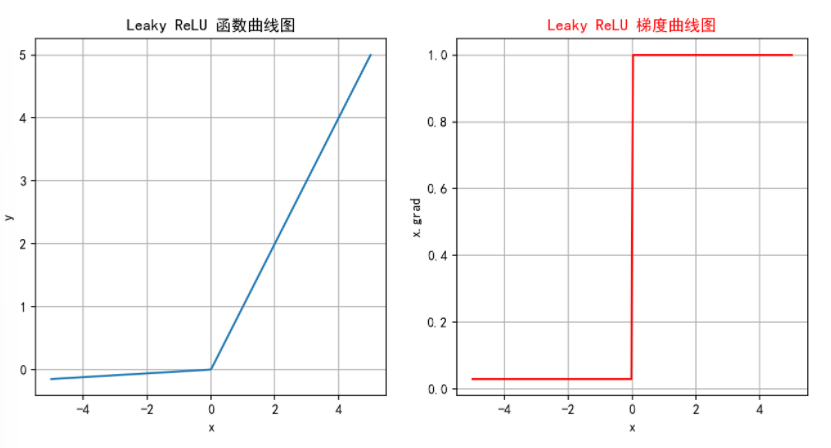
（2）特征

1. 避免神經元死亡：通過在x<=0區域引入一個小的負斜率，這樣即使輸入值小于等于零，Leaky ReLU仍然會有梯度，允許神經元繼續更新權重，避免神經元在訓練過程中完全“死亡”的問題。

2. 計算簡單：Leaky ReLU 的計算與 ReLU 相似，只需簡單的比較和線性運算，計算開銷低。

（3）缺點

1. 參數選擇：alpha是一個需要調整的超參數，選擇合適的alpha值可能需要實驗和調優。

2. 出現負激活：如果alpha設定得不當，仍然可能導致激活值過低

5、softmax

Softmax激活函數通常用于分類問題的輸出層，它能夠將網絡的輸出轉換為概率分布，使得輸出的各個類別的概率之和為 1。Softmax 特別適合用于多分類問題。

（1）公式

假設神經網絡的輸出層有n個節點，每個節點的輸出為z_i，則 Softmax 函數的定義如下：

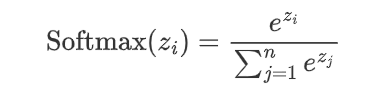
（2）特征

1. 將輸出轉化為概率：通過Softmax，可以將網絡的原始輸出轉化為各個類別的概率，從而可以根據這些概率進行分類決策。

2. 概率分布：Softmax的輸出是一個概率分布，即每個輸出值Softmax（Zi）都是一個介于0和1之間的數，并且所有輸出值的和為 1：

   

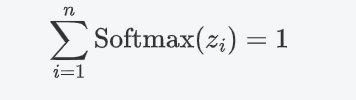
3. 突出差異：Softmax會放大差異，使得概率最大的類別的輸出值更接近1，而其他類別更接近0。

4. 在實際應用中，Softmax常與交叉熵損失函數Cross-Entropy Loss結合使用，用于多分類問題。在反向傳播中，Softmax的導數計算是必需的。

（3）缺點

1. 數值不穩定性：在計算過程中，如果z_i的數值過大，e^{z_i}可能會導致數值溢出。因此在實際應用中，經常會對z_i進行調整，如減去最大值以確保數值穩定。

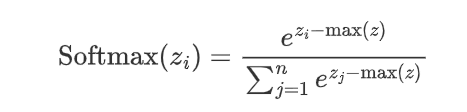
????????2.難以處理大量類別：Softmax在處理類別數非常多的情況下（如大模型中的詞匯表）計算開銷會較大。

（4）代碼實現

import torch
import torch.nn as nn# 表示4分類，每個樣本全連接后得到4個得分，下面示例模擬的是兩個樣本的得分
input_tensor = torch.tensor([[-1.0, 2.0, -3.0, 4.0], [-2, 3, -3, 9]])softmax = nn.Softmax()
output_tensor = softmax(input_tensor)
# 關閉科學計數法
torch.set_printoptions(sci_mode=False)
print("輸入張量:", input_tensor)
print("輸出張量:", output_tensor)
"""
輸入張量: tensor([[-1.,  2., -3.,  4.],[-2.,  3., -3.,  9.]])
輸出張量: tensor([[    0.0059,     0.1184,     0.0008,     0.8749],[    0.0000,     0.0025,     0.0000,     0.9975]])
"""

二、如何選擇激活函數

隱藏層

1. 優先選ReLU；

2. 如果ReLU效果不咋地，那么嘗試其他激活，如Leaky ReLU等；

3. 使用ReLU時注意神經元死亡問題， 避免出現過多神經元死亡；

4. 不使用sigmoid，嘗試使用tanh；

?輸出層

1. 二分類問題選擇sigmoid激活函數；

2. 多分類問題選擇softmax激活函數