注：本文為“光電效應”相關文章合輯。

英文引文，機翻未校。
中文引文，略作重排，未整理去重。
圖片清晰度受引文原圖所限。
如有內容異常，請看原文。

---

Photoelectric Effect

光電效應

Discussion

dilemma

Under the right circumstances light can be used to push electrons, freeing them from the surface of a solid. This process is called the photoelectric effect (or photoelectric emission or photoemission), a material that can exhibit this phenomenon is said to be photoemissive, and the ejected electrons are called photoelectrons; but there is nothing that would distinguish them from other electrons. All electrons are identical to one another in mass, charge, spin, and magnetic moment.
在合適的條件下，光可以用來推動電子，使它們從固體表面脫離。這一過程被稱為光電效應（或光電發射或光發射），能夠表現出這種現象的材料被稱為光電發射性的，被射出的電子被稱為光電子；但它們與其它電子并無區別。所有電子在質量、電荷、自旋和磁矩方面都是相同的。

The photoelectric effect was first observed in 1887 by Heinrich Hertz during experiments with a spark gap generator (the earliest device that could be called a radio). In these experiments, sparks generated between two small metal spheres in a transmitter induce sparks that jump between two different metal spheres in a receiver. Compared to later radio devices, the spark gap generator was notoriously difficult to work with. The air gap would often have to be smaller than a millimeter for the receiver to reliably reproduce the spark of the transmitter. Hertz found that he could increase the sensitivity of his spark gap device by illuminating it with visible or ultraviolet light. Later studies by J.J. Thomson showed that this increased sensitivity was the result of light pushing on electrons — a particle that he discovered in 1897.
光電效應最初是在 1887 年由海因里希?赫茲在進行火花間隙發生器（最早的可以被稱為收音機的裝置）實驗時觀察到的。在這些實驗中，發射機中兩個小金屬球之間產生的火花會感應出接收機中兩個不同的金屬球之間的火花。與后來的收音機設備相比，火花間隙發生器使用起來臭名昭著地困難。為了使接收機能夠可靠地復制發射機的火花，空氣間隙常常必須小于一毫米。赫茲發現，他可以通過用可見光或紫外光照射來提高他的火花間隙裝置的靈敏度。后來，J.J. 湯姆遜的研究表明，這種靈敏度的增加是光推動電子的結果 —— 他于 1897 年發現了這種粒子。

While this is interesting, it is hardly amazing. All forms of electromagnetic radiation transport energy and it is quite easy to imagine this energy being used to push tiny particles of negative charge free from the surface of a metal where they are not all that strongly confined in the first place. The era of modern physics is one of completely unexpected and inexplicable discoveries, however. Subsequent investigations into the photoelectric effect yielded results that did not fit with the classical theory of electromagnetic radiation. When it interacted with electrons, light just didn’t behave like it was supposed to. Repairing this tear in theory required more than just a patch. It meant rebuilding a large portion of physics from the ground up.
盡管這很有趣，但并不令人驚嘆。所有形式的電磁輻射都傳遞能量，很容易想象這種能量被用來將微小的負電荷粒子從金屬表面推開，這些粒子在金屬表面本來就不是被強烈束縛的。然而，現代物理學的時代是一個充滿完全出乎意料且無法解釋的發現的時代。對光電效應的后續研究得出了與經典電磁輻射理論不相符的結果。當光與電子相互作用時，它表現得并不像它本應表現的那樣。修復這一理論上的裂痕需要的不僅僅是打補丁。這意味著要從頭開始重建物理學的大部分內容。

It was Philipp Lenard, an assistant of Hertz, who performed the earliest, definitive studies of the photoelectric effect. Lenard used metal surfaces that were first cleaned and then held under a vacuum so that the effect might be studied on the metal alone and not be affected by any surface contaminants or oxidation. The metal sample was housed in an evacuated glass tube with a second metal plate mounted at the opposite end. The tube was then positioned or constrained in some manner so that light would only shine on the first metal plate — the one made out of photoemissive material under investigation. Such a tube is called a photocell (formally) or an electric eye (informally). Lenard connected his photocell to a circuit with a variable power supply, voltmeter, and microammeter as shown in the schematic diagram below. He then illuminated the photoemissive surface with light of differing frequencies and intensities.
正是赫茲的助手菲利普?萊納德進行了最早的、決定性的光電效應研究。萊納德使用了先清潔后置于真空中的金屬表面，以便在不受任何表面污染物或氧化影響的情況下單獨研究金屬上的這種效應。金屬樣品被放置在一個抽空的玻璃管內，管的另一端安裝著第二塊金屬板。然后，管子以某種方式被定位或約束，以便光線只照射到第一塊金屬板 —— 即正在研究的光電發射材料制成的那塊。這種管子被稱為光電管（正式名稱）或電子眼（非正式名稱）。萊納德將他的光電管連接到一個帶有可變電源、伏特表和微安表的電路中，如下圖所示的示意圖。然后，他用不同頻率和強度的光照射光電發射表面。

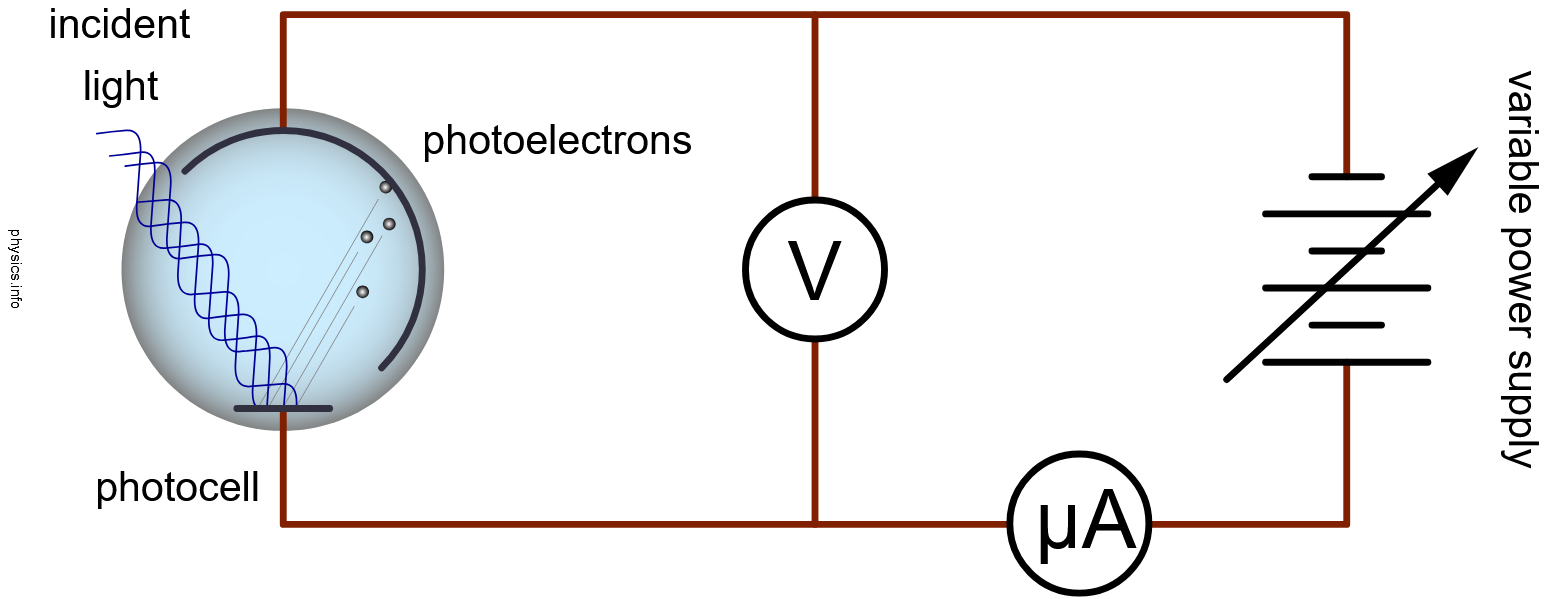
Knocking electrons free from the photoemissive plate would give it a slight positive charge. Since the second plate was connected to the first by the wiring of the circuit, it too would become positive, which would then attract the photoelectrons floating freely through the vacuum where they would land and return back to the plate from which they started. Keep in mind that this experiment doesn’t create electrons out of light, it just uses the energy in light to push electrons that are already there around the circuit. The photoelectric current generated by this means was quite small, but could be measured with the microammeter (a sensitive galvanometer with a maximum deflection of only a few microamps). It also serves as a measure of the rate at which photoelectrons are leaving the surface of the photoemissive material.
從光電發射板上擊出電子會使它略微帶正電。由于第二塊板通過電路的連線與第一塊相連，它也會帶正電，這將吸引在真空中自由漂浮的光電子，它們會落在上面并返回到它們開始的那塊板。請注意，這個實驗并不是從光中創造出電子，它只是利用光中的能量來推動已經在那里的電子在電路中移動。通過這種方式產生的光電流相當小，但可以用微安表（一種靈敏的檢流計，最大偏轉僅為幾微安）測量。它也可以作為光電子離開光電發射材料表面的速率的量度。

Note how the power supply is wired into the circuit — with its negative end connected to the plate that isn’t illuminated. This sets up a potential difference that tries to push the photoelectrons back into the photoemissive surface. When the power supply is set to a low voltage it traps the least energetic electrons, reducing the current through the microammeter. Increasing the voltage drives increasingly more energetic electrons back until finally none of them are able to leave the metal surface and the microammeter reads zero. The potential at which this occurs is called the stopping potential. It is a measure of the maximum kinetic energy of the electrons emitted as a result of the photoelectric effect.
注意電源是如何接入電路的 —— 它的負端連接到未被照亮的那塊板上。這建立了一個電勢差，試圖將光電子推回光電發射表面。當電源設置為低電壓時，它會捕獲能量最低的電子，減少通過微安表的電流。增加電壓會將越來越多能量更高的電子推回，直到最后沒有一個電子能夠離開金屬表面，微安表讀數為零。發生這種情況的電勢被稱為截止電勢。它是由于光電效應而發射的電子的最大動能的量度。

What Lenard found was that the intensity of the incident light had no effect on the maximum kinetic energy of the photoelectrons. Those ejected from exposure to a very bright light had the same energy as those ejected from exposure to a very dim light of the same frequency. In keeping with the law of conservation of energy, however, more electrons were ejected by a bright source than a dim source.
萊納德發現，入射光的強度對光電子的最大動能沒有任何影響。那些被非常強的光照射而射出的電子與被同樣頻率的非常弱的光照射而射出的電子具有相同的能量。然而，根據能量守恒定律，強光源比弱光源射出的電子更多。

Later experiments by others, most notably the American physicist Robert Millikan in 1914, found that light with frequencies below a certain cutoff value, called the threshold frequency, would not eject photoelectrons from the metal surface no matter how bright the source was. These results were completely unexpected. Given that it is possible to move electrons with light and given that the energy in a beam of light is related to its intensity, classical physics would predict that a more intense beam of light would eject electrons with greater energy than a less intense beam no matter what the frequency. This was not the case, however.
后來，其他人進行的實驗，最著名的是美國物理學家羅伯特?密立根在 1914 年的實驗，發現低于某一截止值（稱為閾值頻率）的頻率的光，無論光源有多亮，都不會從金屬表面射出光電子。這些結果是完全出乎意料的。鑒于可以用光移動電子，并且考慮到光束中的能量與其強度有關，經典物理學將預測，無論頻率如何，更強的光束將射出能量更大的電子。然而事實并非如此。

Red light does not eject photoelectrons (even if it is very bright). Green light does eject photoelectrons (even if it is very dim). Blue light ejects photoelectrons with more energy than green light (even if it is very dim).
紅光不會射出光電子（即使它非常亮）。綠光會射出光電子（即使它非常暗）。藍光射出的光電子的能量比綠光射出的光電子的能量更多（即使它非常暗）。

Actually, maybe these results aren’t all that typical. Most elements have threshold frequencies that are ultraviolet and only a few dip down low enough to be green or yellow like the example shown above. The materials with the lowest threshold frequencies are all semiconductors. Some have threshold frequencies in the infrared region of the spectrum.
實際上，也許這些結果并不那么典型。大多數元素的閾值頻率是紫外光頻率，只有少數元素的閾值頻率低到像上面例子中那樣是綠色或黃色光頻率。具有最低閾值頻率的材料都是半導體。其中一些的閾值頻率在紅外光區域。

The classical model of light describes it as a transverse, electromagnetic wave. Of this there was very little doubt at the end of the 19th century. The wave nature of light was confirmed when it was applied successfully to explain such optical phenomena as diffraction, interference, polarization, reflection and refraction. If we can imagine light as waves in an electromagnetic ocean and be quite successful at it, then it wouldn’t be much of a stretch for us to image electrons in a metal surface as something like tethered buoys floating in an electromagnetic harbor. Along come the waves (light) which pull and tug at the buoys (electrons). Weak waves have no effect, but strong ones just might yank a buoy from their mooring and set it adrift. A wave model of light would predict an energy-amplitude relationship and not the energy-frequency relationship described above. Photoelectric experiments describe an electromagnetic ocean where monstrous swells wouldn’t tip over a canoe, but tiny ripples would fling you into the air.
經典光模型將光描述為橫電磁波。在 19 世紀末，人們對這一點幾乎沒有懷疑。當光的波動性質被成功地應用于解釋諸如衍射、干涉、偏振、反射和折射等光學現象時，得到了證實。如果我們能夠成功地將光想象成電磁海洋中的波，那么將金屬表面的電子想象成像系在電磁港灣中漂浮的浮標一樣的東西，也不會太難。波（光）來了，拉扯著浮標（電子）。弱波沒有影響，但強波可能剛好會把一個浮標從它的系泊處拽出來，讓它漂走。光的波模型將預測出能量 - 振幅關系，而不是上述的能量 - 頻率關系。光電實驗描述了一個電磁海洋，在這個海洋中，巨大的涌浪不會使獨木舟傾覆，但微小的漣漪卻會把你拋向空中。

If that wasn’t enough, the photoelectrons seem to pop out of the surface too quickly. When light intensities are very low, the rate at which energy is delivered to the surface is downright sluggish. It should take a while for any one particular electron to capture enough of this diffuse energy to free itself. It should, but it doesn’t. The instant that light with an appropriate frequency of any intensity strikes a photoemissive surface, at least one electron will always pop out immediately $t<10^{?9}$ s. Continuing with the ocean analogy, imagine a harbor full of small boats (electrons). The sea is calm except for tiny ripples on the surface (low intensity, short wavelength light). Most of the boats in the harbor are unaffected by these waves, but one is ripped from the harbor and sent flying upward like a jet aircraft. Something just ain’t right here. No mechanical waves behave like this, but light does.
如果這些還不夠，光電子似乎從表面彈出得太快了。當光強度非常低時，能量傳遞到表面的速率相當緩慢。任何一個特定的電子都應該需要一段時間來捕獲足夠的這種分散的能量以使自己脫離。它應該是這樣的，但它不是。當任何強度的合適頻率的光擊中光電發射表面時，至少會有一個電子會立即彈出 $t<10^{?9}$ s。繼續用海洋類比，想象一個滿是小船（電子）的港口。海面平靜，只有表面有微小的漣漪（低強度，短波長光）。港口里的大多數小船都不受這些波的影響，但有一艘卻被從港口拽出來，像噴氣式飛機一樣向上飛去。這里有些東西不太對勁。沒有機械波會像這樣行為，但光卻會。

new idea

The two factors affecting maximum kinetic energy of photoelectrons are the frequency of the incident radiation and the material on the surface. As shown in the graph below, electron energy increases with frequency in a simple linear manner above the threshold. All three curves have the same slope (equal to Planck’s constant) which shows that the energy-frequency relation is constant for all materials. Below the threshold frequency photoemission does not occur. Each curve has a different intercept on the energy axis, which shows that threshold frequency is a function of the material.
影響光電子最大動能的兩個因素是入射輻射的頻率和表面材料。如下面的圖表所示，電子能量隨頻率的增加而線性增加，超過閾值后增加得更快。所有三條曲線的斜率相同（等于普朗克常數），這表明能量 - 頻率關系對所有材料都是恒定的。低于閾值頻率時，光電發射不會發生。每條曲線在能量軸上的截距都不同，這表明閾值頻率是材料的函數。

The genius that figured out what was going on here was none other than the world’s most famous physicist Albert Einstein. In 1905, Einstein realized that light was behaving as if it was composed of tiny particles (initially called quanta and later called photons) and that the energy of each particle was proportional to the frequency of the electromagnetic radiation that it was a part of. Recall from the previous section of this book that Max Planck invented the notion of quantized electromagnetic radiation as a way to solve a technical problem with idealized sources of electromagnetic radiation called blackbodies. Recall also that Planck did not believe that radiation was actually broken up into little bits as his mathematical analysis showed. He thought the whole thing was just a contrivance that gave him the right answers. The genius of Einstein was in recognizing that Planck’s contrivance was in fact a reasonable description of reality. What we perceive as a continuous wave of electromagnetic radiation is actually a stream of discrete particles.
解開這一現象之謎的天才人物正是世界上最著名的物理學家阿爾伯特?愛因斯坦。1905 年，愛因斯坦意識到，光表現得就好像它是由微小的粒子（最初稱為量子，后來稱為光子）組成的，每個粒子的能量與其所屬的電磁輻射的頻率成正比。回想本書前面部分的內容，馬克斯?普朗克發明了量子化電磁輻射的概念，以解決一種稱為黑體的理想化電磁輻射源的技術問題。再回想一下，普朗克并不相信輻射實際上像他的數學分析所顯示的那樣被分解成小塊。他認為這一切只是一個巧妙的裝置，給了他正確的答案。愛因斯坦的天才之處在于他認識到普朗克的巧妙裝置實際上是對現實的合理描述。我們所感知的連續的電磁輻射波實際上是一股離散粒子的流。

Es scheint mir nun in der Tat, da? die Beobachtungen über die ?schwarze Strahlung?, Photolumineszenz, die Erzeugung von Kathodenstrahlen durch ultraviolettes Licht und andere die Erzeugung bez. Verwandlung des Lichtes betreffende Erscheinungsgruppen besser verstandlich erscheinen unter der Annahme, da? die Energie des Lichtes diskontinuierlich im Raume verteilt sei. Nach der hier ins Auge zu fassenden Annahme ist bei Ausbreitung eines von einem Punkte ausgehenden Lichtstrahles die Energie nicht kontinuierlich auf gr??er und gr??er werdencle R?ume verteilt, sondvern es besteht dieselbe aus einer endlichen Zahl von in Raumpunkten lokalisierten Energiequanten, welche sich bewegen, ohne sich zu teilen und welche nur als Ganze absorbiert und erzeugt werden k?nnen.
?
Albert Einstein, 1905
?
事實上，在我看來，關于 “黑體輻射”、光致發光、紫外線產生陰極射線以及其他涉及光的發射或轉換的現象的觀察結果，如果假設光的能量在空間中是不連續分布的，那么這些現象就可以更好地理解了。根據這里考慮的假設，當從一個點發出的光線傳播時，能量并不是在不斷增大的空間中連續分布的，而是由有限數量的能量量子組成，這些量子在空間中是局部化的，它們在運動時不會被分割，而且只能作為一個整體被吸收或發射。
?
阿爾伯特?愛因斯坦，1905 年

equations

Einstein and Millikan described the photoelectric effect using a formula (in contemporary notation) that relates the maximum kinetic energy $K_{\text{max}}$ of the photoelectrons to the frequency of the absorbed photons $f$ and the threshold frequency $f_0$ of the photoemissive surface.
愛因斯坦和密立根用一個公式（現代符號表示）描述了光電效應，這個公式將光電子的最大動能 $K_{\text{max}}$ 與吸收的光子的頻率 $f$ 以及光電發射表面的閾值頻率 $f_0$ 聯系起來。

$$K_{\text{max}}=h(f?f_0)$$

or if you prefer, to the energy of the absorbed photons $E$ and the work function $?$ of the surface
或者，如果你愿意，也可以將它與吸收的光子的能量 $E$ 和表面的逸出功 $?$ 聯系起來

$$K_{\text{max}}=E??$$

where the first term is the energy of the absorbed photons $E$ with frequency $f$ or wavelength $\lambda$
其中，第一項是吸收的光子的能量 $E$，其頻率為 $f$ 或波長為 $\lambda$

$$E=hf=\frac{hc}{\lambda }$$

and the second term is the work function $?$ of the surface with threshold frequency $f_0$ or threshold wavelength ${\lambda }_0$
第二項是表面的逸出功 $?$，其閾值頻率為 $f_0$ 或閾值波長為 ${\lambda }_0$

$$\phi =h{f}_0=\frac{hc}{{\lambda }_0}$$

The maximum kinetic energy $K_{\text{max}}$ of the photoelectrons (with charge $e$) can be determined from the stopping potential $V_0$.
光電子的最大動能 $K_{\text{max}}$（帶電荷 $e$）可以通過截止電勢 $V_0$ 來確定。

$$V_0=\frac{W}{q}=\frac{K_{\text{max}}}{e}$$

Thus…
因此…

$$K_{\text{max}}=e{V}_0$$

When charge $e$ is given in coulombs, the energy will be calculated in joules. When charge $e$ is given in elementary charges, the energy will be calculated in electron volts. This results in a lot of constants. Use the one that’s most appropriate for your problem.
當電荷 $e$ 以庫侖為單位時，能量將以焦耳為單位計算。當電荷 $e$ 以基本電荷為單位時，能量將以電子伏特為單位計算。這會產生許多常數。使用最適合你問題的那個。

Planck’s constant with variations
普朗克常數的不同形式

	SI units	acceptable non-SI units
$h$	$6.62607015\times 10^{?34}$ J s	$4.135667696\times 10^{?15}$ eV s
$hc$	$1.98644586\times 10^{?25}$ J m	$1,239.841984$ eV nm

Lastly, the rate $\frac{n}{t}$ at which photoelectrons (with charge $e$) are emitted from a photoemissive surface can be determined from the photoelectric current $I$.
最后，光電子（帶電荷 $e$）從光電發射表面發射的速率 $\frac{n}{t}$ 可以通過光電流 $I$ 來確定。

$$I=\frac{q}{t}=\frac{ne}{t}$$

Thus…
因此…

$$\frac{n}{t}=\frac{I}{e}$$

technology

技術應用

• “electric eye”, light meter, movie film audio track
  “電子眼”、光度計、電影膠片音頻軌道
• photoconductivity: an increase in the electrical conductivity of a nonmetallic solid when exposed to electromagnetic radiation. The increase in conductivity is due to the addition of free electrons liberated by collision with photons. The rate at which free electrons are generated and the time they remain free determines the amount of the increase.
  光導性：當暴露在電磁輻射下時，非金屬固體的電導率會增加。電導率的增加是由于光子碰撞產生的自由電子的增加。自由電子產生的速率以及它們保持自由的時間決定了增加的量。
• photovoltaics: the ejected electron travels through the emitting material to enter a solid electrode in contact with the photoemitter (instead of traveling through a vacuum to an anode) leading to the direct conversion of radiant energy to electric energy
  光伏效應：被射出的電子通過發射材料進入與光電發射器接觸的固體電極（而不是通過真空到達陽極），從而直接將輻射能轉換為電能
• photostatic copying
  光靜復印

---

早期量子論和量子力學的準備

光電效應的研究

愛因斯坦最早明確地認識到，普朗克的發現標志了物理學的新紀元。1905 年，愛因斯坦在著名論文《關于光的產生和轉化的一個試探性的觀點》中，發展了普朗克的能量子概念。他提出了光量子假說，并用之于光的發射和轉化上，很好地解釋了光電效應等現象。后來，愛因斯坦稱這篇論文是非常革命的，因為它為研究輻射問題提出了嶄新的觀點。

1 愛因斯坦的光量子理論

愛因斯坦在那篇論文中，總結了光學發展中微粒說和波動說長期爭論的歷史，揭示了經典理論的困境，提出只要把光的能量看成不是連續分布，而是一份一份地集中在一起，就可以作出合理的解釋。他寫道：

“確實現在在我看來，關于黑體輻射、光致發光、紫外光產生陰極射線（按：即光電效應）以及其他一些有關光的產生和轉化的現象的觀察，如果用光的能量在空間中不是連續分布的這種假說來解釋，似乎就更好理解。按照這里所設想的假設，從點光源發射出來的光束的能量在傳播中不是連續分布在越來越大的空間之中，而是由個數有限的、局限在空間各點的能量子所組成，這些能量子能夠運動，但不能再分割，而只能整個地被吸收或產生出來。”[1]

也就是說，光不僅在發射中，而且在傳播過程中以及在與物質的相互作用中，都可以看成能量子。愛因斯坦稱之為光量子，也就是后來所謂的光子（photon）。光子一詞則是 1926 年由路易斯（G. N. Lewis）提出的。

作為光量子理論的一個事例，愛因斯坦提到了光電效應。他解釋說：

“能量子穿透物體的表面層，……最簡單的設想是，一個光量子把它的全部能量給予了單個電子……。一個在物體內部被供給了動能的電子當它到達物體表面時已經失去了它的一部分動能。此外還必須假設，每個電子在離開物體時還必須為它脫離物體做一定量的功 $P$（這是物體的特性值按：即逸出功）。那些在表面上朝著垂直方向被激發的電子，將以最大的法線速度離開物體。”[2]

這樣一些電子離開物體時的動能應為 $h\nu ?P$。

愛因斯坦根據能量轉化與守恒原理提出，如果該物體充電至正電位 $V$，并被零電位所包圍（$V$ 也叫遏止電壓），又如果 $V$ 正好大到足以阻止物體損失電荷，就必有

$$eV=h\nu ?P$$

其中 $e$ 即電子電荷。這就是眾所周知的愛因斯坦光電方程。

愛因斯坦的光量子理論和光電方程，簡潔明了，很有說服力，但是當時卻遭到了冷遇。人們認為這種把光看成粒子的思想與麥克斯韋電磁場理論抵觸，是奇談怪論。甚至量子假說的創始人普朗克也表示反對。1913 年普朗克等人在提名愛因斯坦為普魯士科學院會員時，一方面高度評價愛因斯坦的成就，同時又指出：“有時，他可能在他的思索中失去了目標，如他的光量子假設。”[3]

愛因斯坦提出光量子假設和光電方程，的確是很大膽的，因為當時還沒有足夠的實驗事實來支持他的理論，盡管理論與已有的實驗事實并無矛盾。愛因斯坦非常謹慎，所以論文題目取為一個試探性的觀點（heuristischen gesichtspunkt）。愛因斯坦所謂的“非常革命性的”，實際上指的就是“非常大膽的”。如果我們比較詳細地回顧光電效應的發現史，就會更加佩服愛因斯坦的膽略。

2 光電效應的早期研究

2.1. 光電效應的發現

說來有趣。如果說光電效應是光的粒子性的實驗證據，發現這一效應卻是赫茲（H. Hertz）在研究電磁場的波動性時偶然作出的。這件事發生在 1887 年，當時赫茲正用兩套放電電極做實驗，一套產生振蕩，發出電磁波；另一套充當接收器。為了便于觀察，赫茲偶然把接收器用暗箱罩上，結果發現接受電極間的火花變短了。赫茲工作非常認真，用各種材料放在兩套電極之間，證明這種作用既非電磁的屏蔽作用，也不是可見光的照射，而是紫外線的作用。當紫外線照在負電極上時，效果最為明顯，說明負電極更易于放電。

2.2. 揭示光電效應的機制

赫茲的發現以論文《紫外線對放電的影響》發表于 1887 年[4]。隨即引起了廣泛反響。1888 年，德國物理學家霍爾瓦克斯（W. Hallwachs）、意大利的里奇（A. Righi）和俄國的斯托列托夫（A. G. Staletov）幾乎同時作了新的研究（圖 2 是斯托列托夫的實驗原理圖）。

圖 2 斯托列托夫的實驗原理圖

實驗表明負電極在光照射下（特別是紫外線照射下），會放出帶負電的粒子，形成電流。1889 年，愛耳斯特（J. Elster）和蓋特爾（H. F. Geitel）進一步指出，有些金屬（如鉀、鈉、鋅、鋁等）不但對強弧光有光電效應，對普通太陽光也有同樣效應，而另一些金屬（如錫、銅、鐵）則沒有。對于鋅板，要加 $+2.5$ 伏電壓，才能在光照之下保持絕緣。

1899 年，J. J. 湯姆孫測出了光電流的荷質比（實驗原理如圖 3），

圖 3 J.J.湯姆孫測光電流荷質比的實驗原理圖

計算得光電粒子的荷質比 $\frac{e}{m}$ 與陰極射線的荷質比相近，都是 $10^{11}$ 庫侖 / 千克的數量級。這就肯定光電流和陰極射線實質相同，都是高速運動的電子流。原來光電效應就是由于光，特別是紫外光，照射到金屬表面使金屬內部的自由電子獲得更大的動能，因而從金屬表面逃逸到空間的一種現象。不過，這只是一種定性解釋。要根據經典電磁理論建立定量的光電效應理論，卻遇到了難以克服的困難。特別是 1900 年勒納德的新發現使物理學家感到十分迷惑。

3 勒納德的新發現

勒納德為了研究光電子從金屬表面逸出時所具有的能量，在電極間加反向電壓，直到使光電流截止，從反向電壓的截止值（即遏止電壓）$V$，可以推算電子逸出金屬表面的最大速度。圖 4 是勒納德研究光電效應的實驗裝置。

圖 4 勒納德研究光電效應的實驗裝置圖

入射光照在鋁陰極 A 上，反向電壓加在陽極 E 與 A 之間。陽極中間挖了一個小孔，讓電子束穿過，打到集電極 D 上。

勒納德用不同材料做陰極，用不同光源照射，發現都對遏止電壓有影響，惟獨改變光的強度對遏止電壓沒有影響。電子逸出金屬表面的最大速度與光強無關，這就是勒納德的新發現。

但是這個結論與經典理論是矛盾的。根據經典理論，電子接受光的能量獲得動能，應該是光越強，能量也越大，電子的速度也就越快。

和經典理論有抵觸的實驗事實還不止此，在勒納德之前，人們已經遇到了其他的矛盾，例如：

1. 光的頻率低于某一臨界值時，不論光有多強，也不會產生光電流，可是根據經典理論，應該沒有頻率限制。

2. 光照到金屬表面，光電流立即就會產生，可是根據經典理論，能量總要有一個積累過程。

本來，這些矛盾正是揭露了經典理論的不足，可是，勒納德卻煞費苦心地想出了一個補救辦法，企圖在不違反經典理論的前提下，對上述事實作出解釋。他在 1902 年提出觸發假說，假設在電子的發射過程中，光只起觸發作用，電子原本就是以某一速度在原子內部運動，光照到原子上，只要光的頻率與電子本身的振動頻率一致，就發生共振，所以光只起打開閘門的作用，閘門一旦打開，電子就以其自身的速度從原子內部逸走。他認為，原子里電子的振動頻率是特定的，只有頻率合適的光才能起觸發作用。他還建議，由此也許可以了解原子內部的結構。

勒納德的觸發假說很容易被人們接受，當時頗有影響。1905 年，還沒有當上專利局二級技術員的愛因斯坦提出了光量子理論和光電方程。就在這一年，勒納德因陰極射線的研究獲得了諾貝爾物理學獎。難怪人們沒有對愛因斯坦的光電效應理論給予應有的重視。

4 密立根的光電效應實驗

愛因斯坦的光量子理論沒有及時地得到人們的理解和支持，并不完全是由于勒納德的觸發假說占有壓倒優勢，因為不久這一假說即被勒納德自己的實驗駁倒。愛因斯坦遭到冷遇的根本原因在于傳統觀念束縛了人們的思想，而他提出遏止電壓與頻率成正比的線性關系，并沒有直接的實驗依據。因為測量不同頻率下純粹由光輻射引起的微弱電流是一件十分困難的事。

直到 1916 年，才由美國物理學家密立根（Robert Millikan，1868—1953）作出了全面的驗證。他的實驗非常出色，主要是排除了表面的接觸電位差、氧化膜的影響，獲得了比較好的單色光。他選了三種逸出功較低的材料 Na，K，Li（均為堿金屬）作為光陰極，置于特制的真空管中，分別接受光的照射，同時測其光電流，如圖 5。

圖 5 密立根光電效應實驗裝置原理圖

圖 6 和圖 7 是密立根 1916 年發表的兩張實驗曲線圖。

圖 6 密立根發表的光電流曲線之一（曲線與橫坐標的交點即為遏止電壓）

圖 7 鈉的遏止電壓與頻率成正比（從斜率可算出 $h$ 值）

圖 6 給出 6 種頻率的單色光（對應于汞的 6 根譜線）照射下的光電流曲線，由此所得的遏止電壓值與對應的頻率得到圖 7 中的直線。從直線的斜率求出普朗克常數 $h=6.56\times 10^{?34}$ 焦耳·秒，與普朗克 1900 年從黑體輻射求得的結果符合甚好。愛因斯坦對密立根光電效應實驗作了高度評價，指出：“我感激密立根關于光電效應的研究，它第一次判決性地證明了在光的影響下電子從固體發射與光的振動周期有關，這一量子論的結果是輻射的粒子結構所特有的性質。”

正是由于密立根全面地證實了愛因斯坦的光電方程，光量子理論才開始得到人們的承認。后來他們兩人分別獲得了諾貝爾物理學獎。

密立根的光電實驗是從 1904 年開始的，到 1914 年發表初步成果，歷經十年，在 1923 年的領獎演說中，密立根公開承認自己曾長期抱懷疑態度，他說道：

“經過十年之久的實驗、改進和學習，有時甚至還遇到挫折，在這之后，我把一切努力從一開頭就針對光電子發射能量的精密測量，測量它隨溫度、波長、材料（接觸電動勢）改變的函數關系。與我自己預料的相反，這項工作終于在 1914 年成了愛因斯坦方程在很小的實驗誤差范圍內精確有效的第一次直接實驗證據，并且第一次直接從光電效應測定普朗克常數 $h$。”[5]

密立根并不諱言，他在做光電效應實驗時，本來的目的是希望證明經典理論的正確性，甚至在他宣布證實了光電方程時，他還聲稱要肯定愛因斯坦的光量子理論還為時過早。

密立根對量子理論的保守態度有一定的代表性，說明量子理論在發展過程中遇到的阻力是何等的巨大！

參考

[1]: 愛因斯坦全集，第二卷.湖南科技出版社，2002.132
[2]: 同上注，第 142 頁
[3]: 轉引自：Pais A.Subtle is the Lord…Oxford，1982.382
[4]: Hertz H.Annalen der Physik，vol.31.1887
[5]: Milllikan R A.“Nobel Lecture”in Nobel Lectures：Physics，1922—1941.Elsevier，1965.61

---

大學物理實驗：光電效應

星沉慕江吟 已于 2023-03-10 16:39:32

前言

人類對光學的研究從很早就開始了：17 世紀明確地形成了兩大對立學說，分別是牛頓的微粒說，惠更斯的波動說。由于波動說沒有數學基礎以及牛頓的威望，使得微粒說一直占據上風。在 19 世紀，波動說的正確性得到了證明。19 世紀末，光電效應現象的出現使得愛因斯坦在 20 世紀初提出了光子說：光具有粒子性。

一、光電效應理論介紹

1、什么是光電效應

定義：在光的照射下，物體表面發出電子的現象叫做光電效應。發射出來的電子叫光電子。

2、光電效應規律

1. 光電效應的發生幾乎是瞬時的，時間不超過 10^-9 s。
2. 任何金屬都有一個能產生光電效應的最低照射光頻率，叫做極限頻率。
3. 光電子的最大初動能隨入射光頻率的增大而增大，而與入射光強度無關。
4. 光電流強度與入射光的強度成正比。
   所以：光電效應的發生與否，與光的強弱 無關，與照射時間的長短 無關，與光的頻率、金屬材料的種類 有關。

3、愛因斯坦光電效應方程

1. 逸出功 ：$w$
2. 愛因斯坦光電效應方程：$E_k=hv?w$

二、光電效應實驗

1、實驗原理

1. 單位時間內，受光照的金屬板 釋放出來的電子數 和 入射光的強度 成正比。
2. 光電子從金屬表面逸出時具有一定的動能，光電子的 最大初動能 與 入射光的強度 無關。
3. 光電子從金屬表面逸出時的最大初動能與入射光的頻率成 線性關系。當入射光的頻率 小于 截止頻率時，不管照射光的強度多大，都不會 產生光電效應。

2、實驗目的

1. 了解光電效應的規律，加深對光的量子性的理解。
2. 測量普朗克常數 h。
3. 測量光電管的伏安特性曲線。
4. 測量光電管的光電特性曲線。

三、實驗步驟及數據記錄

（一）、測量普朗克常量 h

1. 將測試儀的電壓選擇按鍵切換至 -4V～0V 檔，然后將電壓調至反向最大，即 -4V 附近。光電流測量檔位調至 $10^{?12}$ A 檔，并按照前述方法調零。
2. 取下遮光蓋，將激光光源移近光電管暗盒，避免環境光射入光電管。將激光光源的光強檔調至第 5 檔，波長檔位調至最短波長，并打開激光光源的工作電源開關。
3. 點亮激光光源，然后從低到高往 0V 電壓方向單向調節電壓（應盡量避免光電流大幅超過零后的回調），直到光電流穩定在 0.0×$10^{?12}$ A，將該波長下此時對應的電壓 U0 的絕對值記錄于表 1 中。
4. 嚴格按照從短波到長波順序，依次調節波長檔，重復步驟 3。

表 1 測量截止電壓 $U_0$ 與光頻率 ν 的關系

波長 λ (nm)	406	450	488	519	635
頻率 $\nu (\times 10^{14}Hz$	7.39	6.67	6.15	5.78	4.72
截止電壓絕對值 $U_0$ (V)	1.352	1.053	0.854	0.657	0.458

（二）、測量光電管的伏安特性曲線和光電特性曲線

1. 移開激光光源，將偏振片安裝在激光光源出光孔上，并用遮光蓋遮住光電管暗盒進光孔。將測試儀的電壓選擇按鍵切換至 -4V～+30V 檔，光電流測量檔位調至 $10^{?11}$ A 檔，將儀器按照前述方法調零。
2. 將激光光源的光強檔調至第 5 檔，選定某波長并點亮 3min，人眼觀察遮光蓋上反射的光斑亮度變化情況，旋轉偏振片，直到光斑亮度最小（注意：避免強光直射人眼），然后鎖緊偏振片。
3. 取下光電管暗盒遮光蓋，將激光光源移近光電管暗盒，避免環境光射入光電管。
4. 將電壓調至 26.0V±0.1V。小心仔細地旋轉偏振片，使光電流在 (100±50)×$10^{?12}$ A 范圍內時鎖緊偏振片。注意：光電流嚴禁超過 200×$10^{?12}$ A，否則影響光電管壽命。
5. 將電壓調回 0.0V±0.1V 等待光電流顯示穩定（約 1min），然后記錄從 0.0V～26.0V（推薦間隔 2.0V）的光電流于表 2 中。
6. 然后依次減小光強檔位，重復步驟 5。

表 2 測量光電管的伏安特性曲線和光電特性曲線 $\lambda =450nm$

UAK(V)		0.0	2.0	4.0	6.0	8.0	10.0	12.0	14.0	16.0	18.0	20.0	22.0	24.0	26.0
光電流I(×10-11A)	1檔	3.8	14.9	23.7	29.4	36.8	43.1	48.1	52.2	55.4	58.9	61.5	64.5	66.8	68.9
	2檔	4.5	17.5	27.8	34.4	43.2	50.6	56.4	61.2	64.9	69.1	72.1	75.7	78.3	80.6
	3檔	5.2	20.1	32.0	39.6	49.7	58.3	64.9	70.5	74.7	79.4	83.4	87.0	90.1	92.8
	4檔	5.8	22.5	36.0	44.5	55.9	65.5	72.8	79.1	83.9	89.1	93.7	97.7	101.6	104.1
	5檔	6.6	24.6	39.6	49.2	61.8	72.4	80.6	87.4	92.7	98.6	103.6	108.1	111.9	115.1

三、數據處理與分析

通過實驗，我們將五個不同波長對應的截止電壓測量出來，利用公式 $v=\frac{c}{\lambda }$ 求出每個波長對應的頻率，繪制出 $|U_0|?v$ 關系曲線，然后利用已知點構造新方程如下：

$U_0=3.5\times 10^{?15}(v?5.78\times 10^{14})+0.714$

1、計算過程：

$eU=W+E=hv$

$\frac{U}{v}=\frac{h}{e}$

$k=\frac{h^{\prime }}{e}=3.5\times 10^{?15}$

$h^{\prime }=ke=3.5\times 10^{?15}\times 1.6\times 10^{?19}=5.6\times 10^{?34}$

$\delta =\frac{|h?h^{\prime }|}{h}=15\%$

2、誤差分析：

最后我們算出來的普朗克常量 h’與實際值存在較大的誤差，這可能由于測量的數據不精準和實驗設備的老舊磨損原因。

3、可視化分析：

以上就是這次實驗的全部內容。

---

科大奧瑞物理實驗——光電效應和普朗克常量的測定

脫脫克克 于 2023-03-28 11:12:21 發布

實驗名稱：光電效應和普朗克常量的測定

1. 實驗目的：

通過實驗了解光電效應的基本規律，并用光電效應法測量普朗克常量。

2. 實驗器材：

• 光電管
• 檢流計（或微電流計）
• 直流電壓計
• 直流電源
• 濾波片組
• 光源（汞燈）

3. 實驗原理

當光照在物體上時，光的能量僅部分地以熱的形式被物體吸收，而另一部分則轉換為物體中某些電子的能量，使電子逸出物體表面，這種現象稱為光電效應，逸出的電子稱為光電子。在光電效應中，光顯示出它的粒子性質，所以這種現象對認識光的本性，具有極其重要的意義。

光電效應實驗原理如圖 1 所示。其中 S 為真空光電管，K 為陰極，A 為陽極。當無光照射陰極時，由于陽極與陰極是斷路，所以檢流計 G 中無電流流過，當用一波長比較短的單色光照射到陰極 K 上時，形成光電流，光電流隨加速電位差 U 變化的伏安特性曲線如圖 2 所示。

因此，用光電效應方法測量普朗克常量的關鍵在于獲得單色光、測得光電管的伏安特性曲線和確定遏止電位差值。

實驗中，單色光可由水銀燈光源經過單色儀選擇譜線產生。水銀燈是一種氣體放電光源，點燃穩定后，在可見光區域內有幾條波長相差較遠的強譜線，如表 1 所示。單色儀的鼓輪讀數與出射光的波長存在一一對應關系，由單色儀的定標曲線，即可查出出射單色光的波長（有關單色儀的結構和使用方法請參閱有關說明書），也可用水銀燈（或白熾燈）與濾光片聯合作用產生單色光。

為了獲得準確的遏止電位差值，本實驗用的光電管應該具備下列條件：

1. 對所有可見光譜都比較靈敏。
2. 陽極包圍陰極，這樣當陽極為負電位時，大部分光電子仍能射到陽極。
3. 陽極沒有光電效應，不會產生反向電流。
4. 暗電流很小。

但是實際使用的真空型光電管并不完全滿足以上條件。由于存在陽極光電效應所引起的反向電流和暗電流（即無光照射時的電流），所以測得的電流值，實際上包括上述兩種電流和由陰極光電效應所產生的正向電流三個部分，所以伏安曲線并不與 U 軸相切。由于暗電流是由陰極的熱電子發射及光電管管殼漏電等原因產生，與陰極正向光電流相比，其值很小，且基本上隨電位差 U 呈線性變化，因此可忽略其對遏止電位差的影響。陽極反向光電流雖然在實驗中較顯著，但它服從一定規律。據此，確定遏止電位差值，可采用以下兩種方法。

• 交點法：
  光電管陽極用逸出功較大的材料制作，制作過程中盡量防止陰極材料蒸發，實驗前對光電管陽極通電，減少其上濺射的陰極材料，實驗中避免入射光直接照射到陽極上，這樣可使它的反向電流大大減少，其伏安特性曲線與圖 2 十分接近，因此曲線與 U 軸交點的電位差近似等于遏止電位差，此即交點法。

• 拐點法：
  光電管陽極反向光電流雖然較大，但在結構設計上，若是反向光電流能較快地飽和，則伏安特性曲線在反向電流進入飽和段后有著明顯的拐點，如圖 3 所示，此拐點的電位差即為遏止電位差。

4. 實驗內容與步驟

在 577.0nm、546.1nm、435.8nm、404.7nm 四種單色光下分別測出光電管的伏安特性曲線，并根據此曲線確定遏止電位差值，計算普朗克常量。

本實驗所用儀器有：光電管、單色儀（或濾波片）、水銀燈、檢流計（或微電流計）、直流電源、直流電壓計等，接線電路圖如圖 4 所示。實驗中提供的光電效應測試儀，除光電管 S 外，線路已連接好。

實驗中光電流比較微弱，其值與光電管類型，單色光強弱等因素有關，因此應根據實際情況選用合適的測量儀器。例如，選用 GD-4、GD-5、或 1977 型光電管，選用的檢流計的分度值應在 A/分度左右。如果要測量更微弱的電流可用微電流計，可測量 A 的電流。

由于光電管的內阻很高，光電流如此之微弱，因此測量中要注意抗外界電磁干擾。并避免光直接照射陽極和防止雜散光干擾。

作 U-v 的關系曲線，用一元線性回歸法計算光電管陰極材料的紅限頻率、逸出功及 h 值，并與公認值比較。

n 測定光電管的光電特性曲線，即飽和光電流與照射光強度的關系，實驗室提供有透光率 50%，25%，10% 的濾光片，請用 577.0nm 波長為光源，在光電管、光源位置固定時，測光電管的正向伏安特性曲線，驗證飽和電流與光強關系。

本實驗所用儀器有：光電管、濾波片、濾光片、水銀燈、檢流計（或微電流計）、直流電源、直流電壓計等。

5. 實驗記錄

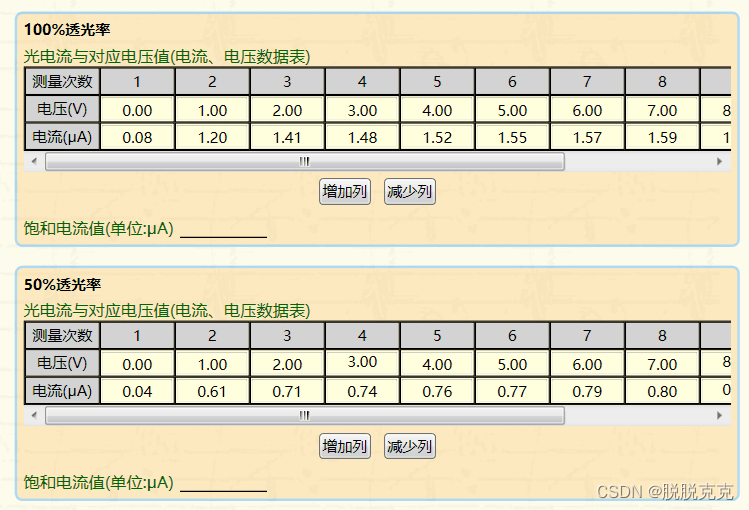
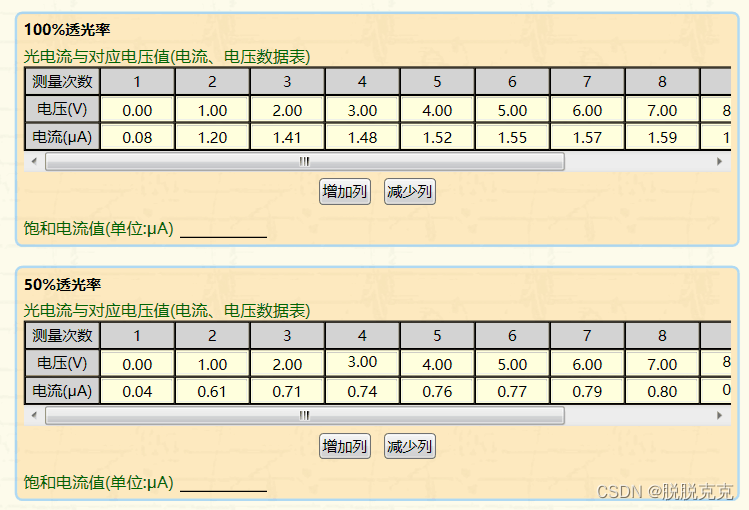
6. 數據處理及誤差分析

1. 計算普朗克常數

根據實驗測得的數據繪制

$h{v}_1=e|U_1|+A$
$h{v}_2=e|U_2|+A$
……

$h{v}_n=e|U_n|+A$

由以上公式得知，直線斜率 $k=\frac{h}{e}$，求出直線斜率，就可算出普朗克常數 $h$，繪制截止電壓與頻率的圖像并進行擬合得到：

由圖中斜率得：$h=6.88\times 10^{?34}$；
相對誤差為 5.84%。

2. 驗證飽和電流與光強關系

由圖可得，飽和電流分別為：

• $1.65\times 10^{?3}$ A
• $0.83\times 10^{?3}$ A
• $0.42\times 10^{?3}$ A
• $0.17\times 10^{?3}$ A

飽和電流與光照強度成線性關系，驗證成功。

---

via：

• 光電效應的研究
  https://enjoyphysics.cn/Article3272

• （大學物理實驗）光電效應_光電效應實驗-CSDN博客
  https://blog.csdn.net/m0_62469457/article/details/129432790

• 科大奧瑞物理實驗——光電效應和普朗克常量的測定_普朗克常量測定u—v圖-CSDN博客
  https://blog.csdn.net/m0_46808930/article/details/129812086

• 光電效應測普朗克常數 h
  https://phylab.qut.edu.cn/__local/4/FC/B4/25967BEFF162E8E45C5EE9F78DF_68FCB4C4_A50D6.pdf?e=.pdf

• 康普頓效應證明了光的粒子性嗎？ - 知乎
  https://www.zhihu.com/question/433938150

• Photoelectric Effect – The Physics Hypertextbook
  https://physics.info/photoelectric/

• 6.3: Photoelectric Effect - Physics LibreTexts
  https://phys.libretexts.org/Bookshelves/University_Physics/University_Physics_(OpenStax)/University_Physics_III_-_Optics_and_Modern_Physics_(OpenStax)/06%3A_Photons_and_Matter_Waves/6.03%3A_Photoelectric_Effect