一、GM與LSTM的基本原理及互補性
1. GM模型的核心特點
-
基本原理：通過累加生成（AGO）將原始無序序列轉化為具有指數規律的光滑序列，建立一階微分方程（如GM(1,1)）進行預測。其數學形式為：
dx(1)dt+ax(1)=b \frac{dx^{(1)}}{dt} + ax^{(1)} = b dtdx(1)?+ax(1)=b其中 x(1)x^{(1)}x(1) 為累加序列，a,ba, ba,b 為待估參數。
-
優勢：
- 小樣本需求（≥4個數據點）；
- 不依賴數據分布假設，適用隨機性強、信息不全的“灰色系統”；
- 計算效率高，適合短期至中期預測。
-
局限：長期預測精度下降，對非線性關系捕捉不足。
2. LSTM的核心特點
-
基本原理：通過遺忘門、輸入門、輸出門控制細胞狀態（長期記憶），解決傳統RNN的梯度消失問題。核心公式包括：
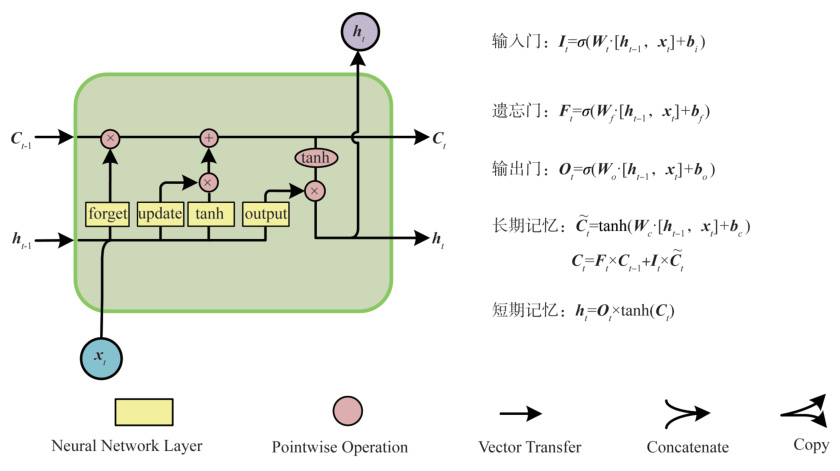
ft=σ(Wf?[ht?1,xt]+bf)it=σ(Wi?[ht?1,xt]+bi)ot=σ(Wo?[ht?1,xt]+bo)C~t=tanh?(WC?[ht?1,xt]+bC)Ct=ft⊙Ct?1+it⊙C~tht=ot⊙tanh?(Ct) \begin{align*} f_t &= \sigma(W_f \cdot [h_{t-1}, x_t] + b_f) \\ i_t &= \sigma(W_i \cdot [h_{t-1}, x_t] + b_i) \\ o_t &= \sigma(W_o \cdot [h_{t-1}, x_t] + b_o) \\ \tilde{C}_t &= \tanh(W_C \cdot [h_{t-1}, x_t] + b_C) \\ C_t &= f_t \odot C_{t-1} + i_t \odot \tilde{C}_t \\ h_t &= o_t \odot \tanh(C_t) \end{align*} ft?it?ot?C~t?Ct?ht??=σ(Wf??[ht?1?,xt?]+bf?)=σ(Wi??[ht?1?,xt?]+bi?)=σ(Wo??[ht?1?,xt?]+bo?)=tanh(WC??[ht?1?,xt?]+bC?)=ft?⊙Ct?1?+it?⊙C~t?=ot?⊙tanh(Ct?)? -
優勢：
- 捕捉長期依賴關系，適合復雜非線性序列；
- 在時間序列預測（如股價、風速）中表現卓越。
-
局限：需大量訓練數據，計算成本高，對參數敏感。
3. 互補性分析
- GM提供數據預處理能力：將原始序列轉化為規律性更強的累加序列，降低噪聲影響；
- LSTM提供非線性建模能力：學習GM殘差中的復雜模式；
- 結合方式：GM提取趨勢項，LSTM擬合殘差項，或通過加權融合預測結果。
二、GM+LSTM組合模型的實現框架
- 步驟：
- GM預測原始序列，得到趨勢分量 y^GM\hat{y}_{\text{GM}}y^?GM?；
- 計算殘差序列 ?=y?y^GM\epsilon = y - \hat{y}_{\text{GM}}?=y?y^?GM?；
- LSTM訓練殘差序列，預測殘差值 ?^\hat{\epsilon}?^；
- 最終預測：y^=y^GM+?^\hat{y} = \hat{y}_{\text{GM}} + \hat{\epsilon}y^?=y^?GM?+?^。
三、代碼獲取
私信回復MATLAB基于GM（灰色模型）與LSTM（長短期記憶網絡）的組合預測方法
