代碼隨想錄算法訓練營第70天圖論9[1]

代碼隨想錄算法訓練營第70天:圖論9

拓撲排序精講

卡碼網：117. 軟件構建(opens new window)

題目描述：

某個大型軟件項目的構建系統擁有 N 個文件，文件編號從 0 到 N - 1，在這些文件中，某些文件依賴于其他文件的內容，這意味著如果文件 A 依賴于文件 B，則必須在處理文件 A 之前處理文件 B （0 <= A, B <= N - 1）。請編寫一個算法，用于確定文件處理的順序。

輸入描述：

第一行輸入兩個正整數 M, N。表示 N 個文件之間擁有 M 條依賴關系。

后續 M 行，每行兩個正整數 S 和 T，表示 T 文件依賴于 S 文件。

輸出描述：

輸出共一行，如果能處理成功，則輸出文件順序，用空格隔開。

如果不能成功處理（相互依賴），則輸出 -1。

輸入示例：

輸出示例：

0 1 2 3 4

提示信息：

文件依賴關系如下：

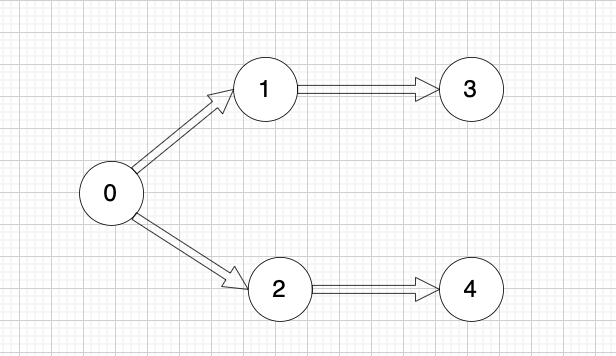所以，文件處理的順序除了示例中的順序，還存在

0 2 4 1 3

0 2 1 3 4

等等合法的順序。

數據范圍：

0 <= N <= 10 ^ 5
1 <= M <= 10 ^ 9

#拓撲排序的背景

本題是拓撲排序的經典題目。

一聊到拓撲排序，一些錄友可能會想這是排序，不會想到這是圖論算法。

其實拓撲排序是經典的圖論問題。

先說說拓撲排序的應用場景。

大學排課，例如先上A課，才能上B課，上了B課才能上C課，上了A課才能上D課，等等一系列這樣的依賴順序。問給規劃出一條完整的上課順序。

拓撲排序在文件處理上也有應用，我們在做項目安裝文件包的時候，經常發現復雜的文件依賴關系， A依賴B，B依賴C，B依賴D，C依賴E 等等。

如果給出一條線性的依賴順序來下載這些文件呢？

有錄友想上面的例子都很簡單啊，我一眼能給排序出來。

那如果上面的依賴關系是一百對呢，一千對甚至上萬個依賴關系，這些依賴關系中可能還有循環依賴，你如何發現循環依賴呢，又如果排出線性順序呢。

所以拓撲排序就是專門解決這類問題的。

概括來說，給出一個有向圖，把這個有向圖轉成線性的排序就叫拓撲排序。

當然拓撲排序也要檢測這個有向圖是否有環，即存在循環依賴的情況，因為這種情況是不能做線性排序的。

所以拓撲排序也是圖論中判斷有向無環圖的常用方法。

#拓撲排序的思路

拓撲排序指的是一種解決問題的大體思路，而具體算法，可能是廣搜也可能是深搜。

大家可能發現各式各樣的解法，糾結哪個是拓撲排序？

其實只要能在把有向無環圖進行線性排序的算法都可以叫做拓撲排序。

實現拓撲排序的算法有兩種：卡恩算法（BFS）和DFS

卡恩1962年提出這種解決拓撲排序的思路

一般來說我們只需要掌握 BFS （廣度優先搜索）就可以了，清晰易懂，如果還想多了解一些，可以再去學一下 DFS 的思路，但 DFS 不是本篇重點。

接下來我們來講解BFS的實現思路。

以題目中示例為例如圖：

做拓撲排序的話，如果肉眼去找開頭的節點，一定能找到節點0 吧，都知道要從節點0 開始。

但為什么我們能找到節點0呢，因為我們肉眼看著這個圖就是從節點0出發的。

作為出發節點，它有什么特征？

你看節點0 的入度為0 出度為2，也就是沒有邊指向它，而它有兩條邊是指出去的。

節點的入度表示有多少條邊指向它，節點的出度表示有多少條邊從該節點出發。

所以當我們做拓撲排序的時候，應該優先找入度為 0 的節點，只有入度為0，它才是出發節點。 理解以上內容很重要！

接下來我給出拓撲排序的過程，其實就兩步：

找到入度為0 的節點，加入結果集
將該節點從圖中移除

循環以上兩步，直到所有節點都在圖中被移除了。

結果集的順序，就是我們想要的拓撲排序順序（結果集里順序可能不唯一）

#模擬過程

用本題的示例來模擬這一過程：

1、找到入度為0 的節點，加入結果集

2、將該節點從圖中移除

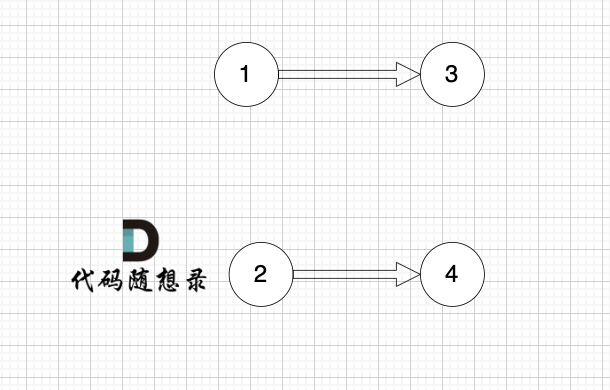1、找到入度為0 的節點，加入結果集

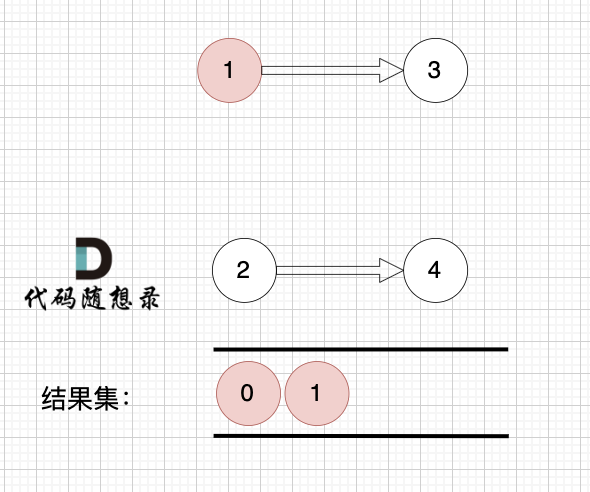這里大家會發現，節點1 和節點2 入度都為0，選哪個呢？

選哪個都行，所以這也是為什么拓撲排序的結果是不唯一的。

2、將該節點從圖中移除

1、找到入度為0 的節點，加入結果集

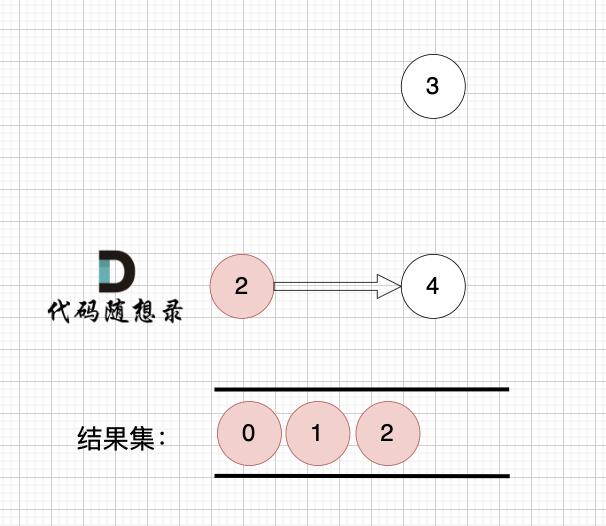節點2 和節點3 入度都為0，選哪個都行，這里選節點2

2、將該節點從圖中移除

后面的過程一樣的，節點3 和節點4，入度都為0，選哪個都行。

最后結果集為： 0 1 2 3 4 。當然結果不唯一的。

#判斷有環

如果有有向環怎么辦呢？例如這個圖：

這個圖，我們只能將入度為0 的節點0 接入結果集。

之后，節點1、2、3、4 形成了環，找不到入度為0 的節點了，所以此時結果集里只有一個元素。

那么如果我們發現結果集元素個數不等于圖中節點個數，我們就可以認定圖中一定有有向環！

這也是拓撲排序判斷有向環的方法。

通過以上過程的模擬大家會發現這個拓撲排序好像不難，還有點簡單。

#寫代碼

理解思想后，確實不難，但代碼寫起來也不容易。

為了每次可以找到所有節點的入度信息，我們要在初始話的時候，就把每個節點的入度和每個節點的依賴關系做統計。

代碼如下：

cin >> n >> m;
vector<int> inDegree(n, 0); // 記錄每個文件的入度
vector<int> result; // 記錄結果
unordered_map<int, vector<int>> umap; // 記錄文件依賴關系while (m--) {
// s->t，先有s才能有t
cin >> s >> t;
inDegree[t]++; // t的入度加一
umap[s].push_back(t); // 記錄s指向哪些文件
}

找入度為0 的節點，我們需要用一個隊列放存放。

因為每次尋找入度為0的節點，不一定只有一個節點，可能很多節點入度都為0，所以要將這些入度為0的節點放到隊列里，依次去處理。

代碼如下：


queue<int> que;
for (int i = 0; i < n; i++) {
// 入度為0的節點，可以作為開頭，先加入隊列
if (inDegree[i] == 0) que.push(i);
}

開始從隊列里遍歷入度為0 的節點，將其放入結果集。


while (que.size()) {
int  cur = que.front(); // 當前選中的節點
que.pop();
result.push_back(cur);
// 將該節點從圖中移除 }

這里面還有一個很重要的過程，如何把這個入度為0的節點從圖中移除呢？

首先我們為什么要把節點從圖中移除？

為的是將該節點作為出發點所連接的邊刪掉。

刪掉的目的是什么呢？

要把該節點作為出發點所連接的節點的入度減一。

如果這里不理解，看上面的模擬過程第一步：

這事節點1 和節點2 的入度為 1。

將節點0刪除后，圖為這樣：

那么節點0 作為出發點所連接的節點的入度就都做了減一的操作。

此時節點1 和節點 2 的入度都為0，這樣才能作為下一輪選取的節點。

所以，我們在代碼實現的過程中，本質是要將該節點作為出發點所連接的節點的入度減一就可以了，這樣好能根據入度找下一個節點，不用真在圖里把這個節點刪掉。

該過程代碼如下：


while (que.size()) {
int  cur = que.front(); // 當前選中的節點
que.pop();
result.push_back(cur);
// 將該節點從圖中移除 
vector<int> files = umap[cur]; //獲取cur指向的節點
if (files.size()) { // 如果cur有指向的節點
for (int i = 0; i < files.size(); i++) { // 遍歷cur指向的節點
inDegree[files[i]] --; // cur指向的節點入度都做減一操作
// 如果指向的節點減一之后，入度為0，說明是我們要選取的下一個節點，放入隊列。
if(inDegree[files[i]] == 0) que.push(files[i]); 
}
}}

最后代碼如下：

#include <iostream>
#include <vector>
#include <queue>
#include <unordered_map>
using namespace std;
int main() {
int m, n, s, t;
cin >> n >> m;
vector<int> inDegree(n, 0); // 記錄每個文件的入度unordered_map<int, vector<int>> umap;// 記錄文件依賴關系
vector<int> result; // 記錄結果while (m--) {
// s->t，先有s才能有t
cin >> s >> t;
inDegree[t]++; // t的入度加一
umap[s].push_back(t); // 記錄s指向哪些文件
}
queue<int> que;
for (int i = 0; i < n; i++) {
// 入度為0的文件，可以作為開頭，先加入隊列
if (inDegree[i] == 0) que.push(i);
//cout << inDegree[i] << endl;
}
// int count = 0;
while (que.size()) {
int  cur = que.front(); // 當前選中的文件
que.pop();
//count++;
result.push_back(cur);
vector<int> files = umap[cur]; //獲取該文件指向的文件
if (files.size()) { // cur有后續文件
for (int i = 0; i < files.size(); i++) {
inDegree[files[i]] --; // cur的指向的文件入度-1
if(inDegree[files[i]] == 0) que.push(files[i]);
}
}
}
if (result.size() == n) {
for (int i = 0; i < n - 1; i++) cout << result[i] << " ";
cout << result[n - 1];
} else cout << -1 << endl;}

dijkstra（樸素版）精講

卡碼網：47. 參加科學大會(opens new window)

【題目描述】

小明是一位科學家，他需要參加一場重要的國際科學大會，以展示自己的最新研究成果。

小明的起點是第一個車站，終點是最后一個車站。然而，途中的各個車站之間的道路狀況、交通擁堵程度以及可能的自然因素（如天氣變化）等不同，這些因素都會影響每條路徑的通行時間。

小明希望能選擇一條花費時間最少的路線，以確保他能夠盡快到達目的地。

【輸入描述】

第一行包含兩個正整數，第一個正整數 N 表示一共有 N 個公共汽車站，第二個正整數 M 表示有 M 條公路。

接下來為 M 行，每行包括三個整數，S、E 和 V，代表了從 S 車站可以單向直達 E 車站，并且需要花費 V 單位的時間。

【輸出描述】

輸出一個整數，代表小明從起點到終點所花費的最小時間。

輸入示例

輸出示例：12

【提示信息】

能夠到達的情況：

如下圖所示，起始車站為 1 號車站，終點車站為 7 號車站，綠色路線為最短的路線，路線總長度為 12，則輸出 12。

不能到達的情況：

如下圖所示，當從起始車站不能到達終點車站時，則輸出 -1。

? 外鏈圖片轉存失敗,源站可能有防盜鏈機制,建議將圖片保存下來直接上傳 ?

數據范圍：

1 <= N <= 500; 1 <= M <= 5000;

#思路

本題就是求最短路，最短路是圖論中的經典問題即：給出一個有向圖，一個起點，一個終點，問起點到終點的最短路徑。

接下來，我們來詳細講解最短路算法中的 dijkstra 算法。

dijkstra算法：在有權圖（權值非負數）中求從起點到其他節點的最短路徑算法。

需要注意兩點：

dijkstra 算法可以同時求起點到所有節點的最短路徑
權值不能為負數

（這兩點后面我們會講到）

如本題示例中的圖：

起點（節點1）到終點（節點7）的最短路徑是圖中標記綠線的部分。

最短路徑的權值為12。

其實 dijkstra 算法和我們之前講解的prim算法思路非常接近，如果大家認真學過prim算法，那么理解 Dijkstra 算法會相對容易很多。（這也是我要先講prim再講dijkstra的原因）

dijkstra 算法同樣是貪心的思路，不斷尋找距離源點最近的沒有訪問過的節點。

這里我也給出 dijkstra三部曲：

第一步，選源點到哪個節點近且該節點未被訪問過
第二步，該最近節點被標記訪問過
第三步，更新非訪問節點到源點的距離（即更新minDist數組）

大家此時已經會發現，這和prim算法怎么這么像呢。

我在prim算法講解中也給出了三部曲。 prim 和 dijkstra 確實很像，思路也是類似的，這一點我在后面還會詳細來講。

在dijkstra算法中，同樣有一個數組很重要，起名為：minDist。

minDist數組用來記錄每一個節點距離源點的最小距離。

理解這一點很重要，也是理解 dijkstra 算法的核心所在。

大家現在看著可能有點懵，不知道什么意思。

沒關系，先讓大家有一個印象，對理解后面講解有幫助。

我們先來畫圖看一下 dijkstra 的工作過程，以本題示例為例：（以下為樸素版dijkstra的思路）

（示例中節點編號是從1開始，所以為了讓大家看的不暈，minDist數組下標我也從 1 開始計數，下標0 就不使用了，這樣下標和節點標號就可以對應上了，避免大家搞混）

#樸素版dijkstra

#模擬過程

0、初始化

minDist數組數值初始化為int最大值。

這里在強點一下 minDist數組的含義：記錄所有節點到源點的最短路徑，那么初始化的時候就應該初始為最大值，這樣才能在后續出現最短路徑的時候及時更新。

（圖中，max 表示默認值，節點0 不做處理，統一從下標1 開始計算，這樣下標和節點數值統一，方便大家理解，避免搞混）

源點（節點1）到自己的距離為0，所以 minDist[1] = 0

此時所有節點都沒有被訪問過，所以 visited數組都為0

以下為dijkstra 三部曲

1、選源點到哪個節點近且該節點未被訪問過

源點距離源點最近，距離為0，且未被訪問。

2、該最近節點被標記訪問過

標記源點訪問過

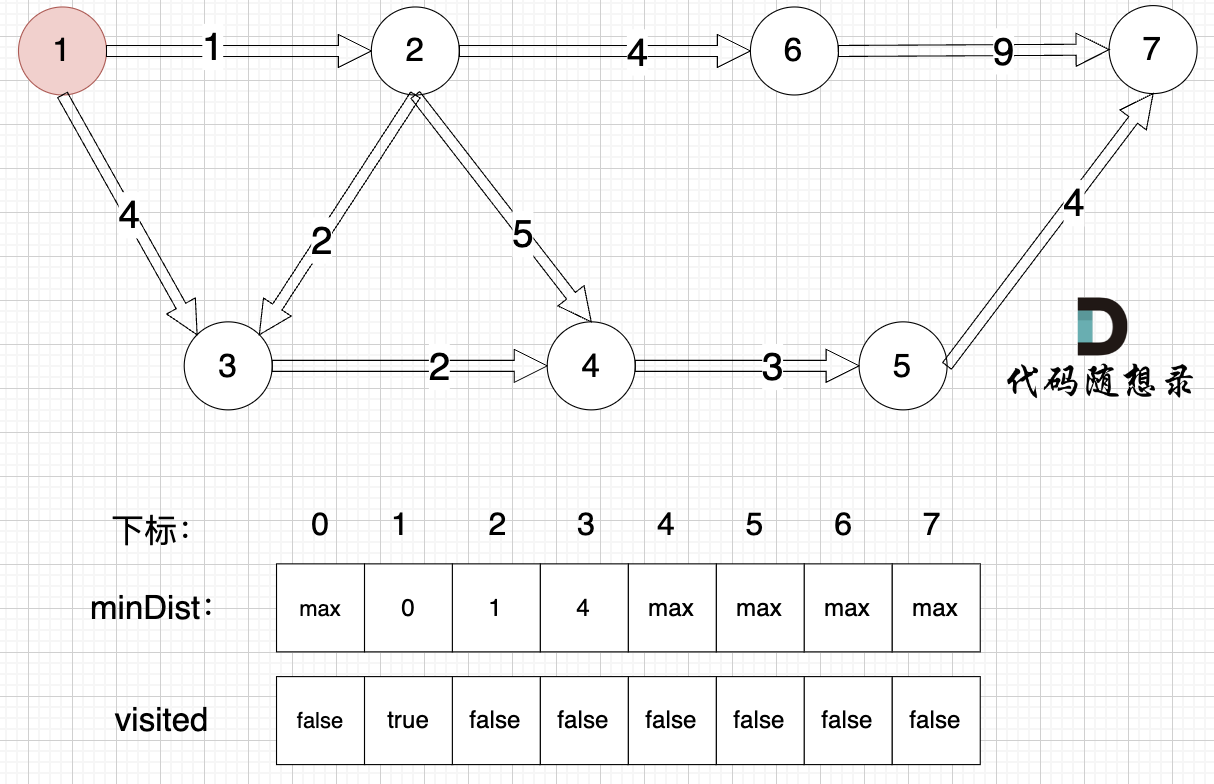
3、更新非訪問節點到源點的距離（即更新minDist數組），如圖：

更新 minDist數組，即：源點（節點1）到節點2 和節點3的距離。

源點到節點2的最短距離為1，小于原minDist[2]的數值max，更新minDist[2] = 1
源點到節點3的最短距離為4，小于原minDist[3]的數值max，更新minDist[4] = 4

可能有錄友問：為啥和 minDist[2] 比較？

再強調一下 minDist[2] 的含義，它表示源點到節點2的最短距離，那么目前我們得到了源點到節點2的最短距離為1，小于默認值max，所以更新。 minDist[3]的更新同理

1、選源點到哪個節點近且該節點未被訪問過

未訪問過的節點中，源點到節點2距離最近，選節點2

2、該最近節點被標記訪問過

節點2被標記訪問過

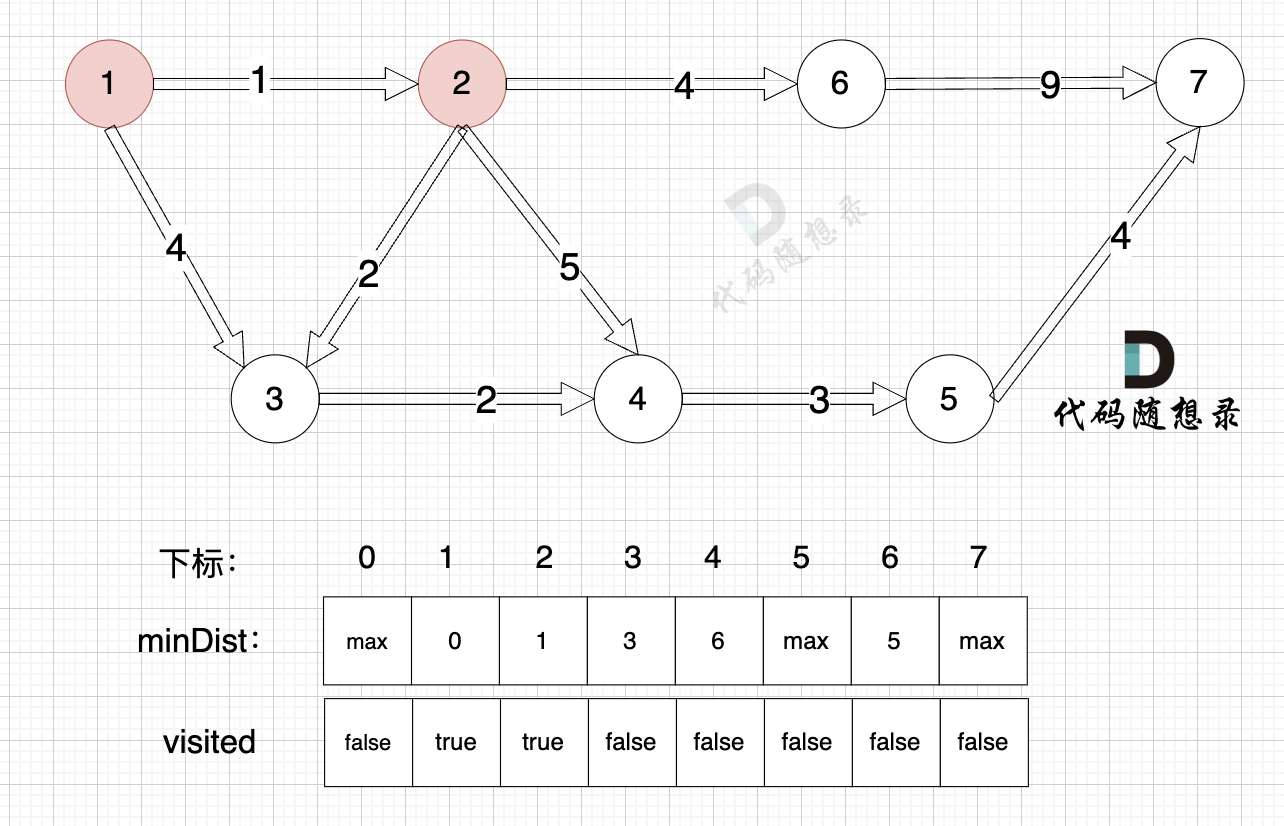
3、更新非訪問節點到源點的距離（即更新minDist數組），如圖：

更新 minDist數組，即：源點（節點1）到節點6 、節點3 和節點4的距離。

為什么更新這些節點呢？怎么不更新其他節點呢？

因為源點（節點1）通過已經計算過的節點（節點2）可以鏈接到的節點有節點3，節點4和節點6.

更新 minDist數組：

源點到節點6的最短距離為5，小于原minDist[6]的數值max，更新minDist[6] = 5
源點到節點3的最短距離為3，小于原minDist[3]的數值4，更新minDist[3] = 3
源點到節點4的最短距離為6，小于原minDist[4]的數值max，更新minDist[4] = 6

1、選源點到哪個節點近且該節點未被訪問過

未訪問過的節點中，源點距離哪些節點最近，怎么算的？

其實就是看 minDist數組里的數值，minDist 記錄了源點到所有節點的最近距離，結合visited數組篩選出未訪問的節點就好。

從上面的圖，或者從minDist數組中，我們都能看出未訪問過的節點中，源點（節點1）到節點3距離最近。

2、該最近節點被標記訪問過

節點3被標記訪問過

3、更新非訪問節點到源點的距離（即更新minDist數組），如圖：

由于節點3的加入，那么源點可以有新的路徑鏈接到節點4 所以更新minDist數組：

更新 minDist數組：

源點到節點4的最短距離為5，小于原minDist[4]的數值6，更新minDist[4] = 5

1、選源點到哪個節點近且該節點未被訪問過

距離源點最近且沒有被訪問過的節點，有節點4 和節點6，距離源點距離都是 5 （minDist[4] = 5，minDist[6] = 5），選哪個節點都可以。

2、該最近節點被標記訪問過

節點4被標記訪問過

3、更新非訪問節點到源點的距離（即更新minDist數組），如圖：

由于節點4的加入，那么源點可以鏈接到節點5 所以更新minDist數組：

源點到節點5的最短距離為8，小于原minDist[5]的數值max，更新minDist[5] = 8

1、選源點到哪個節點近且該節點未被訪問過

距離源點最近且沒有被訪問過的節點，是節點6，距離源點距離是 5 （minDist[6] = 5）

2、該最近節點被標記訪問過

節點6 被標記訪問過

3、更新非訪問節點到源點的距離（即更新minDist數組），如圖：

由于節點6的加入，那么源點可以鏈接到節點7 所以更新minDist數組：

源點到節點7的最短距離為14，小于原minDist[7]的數值max，更新minDist[7] = 14

1、選源點到哪個節點近且該節點未被訪問過

距離源點最近且沒有被訪問過的節點，是節點5，距離源點距離是 8 （minDist[5] = 8）

2、該最近節點被標記訪問過

節點5 被標記訪問過

3、更新非訪問節點到源點的距離（即更新minDist數組），如圖：

由于節點5的加入，那么源點有新的路徑可以鏈接到節點7 所以更新minDist數組：

源點到節點7的最短距離為12，小于原minDist[7]的數值14，更新minDist[7] = 12

1、選源點到哪個節點近且該節點未被訪問過

距離源點最近且沒有被訪問過的節點，是節點7（終點），距離源點距離是 12 （minDist[7] = 12）

2、該最近節點被標記訪問過

節點7 被標記訪問過

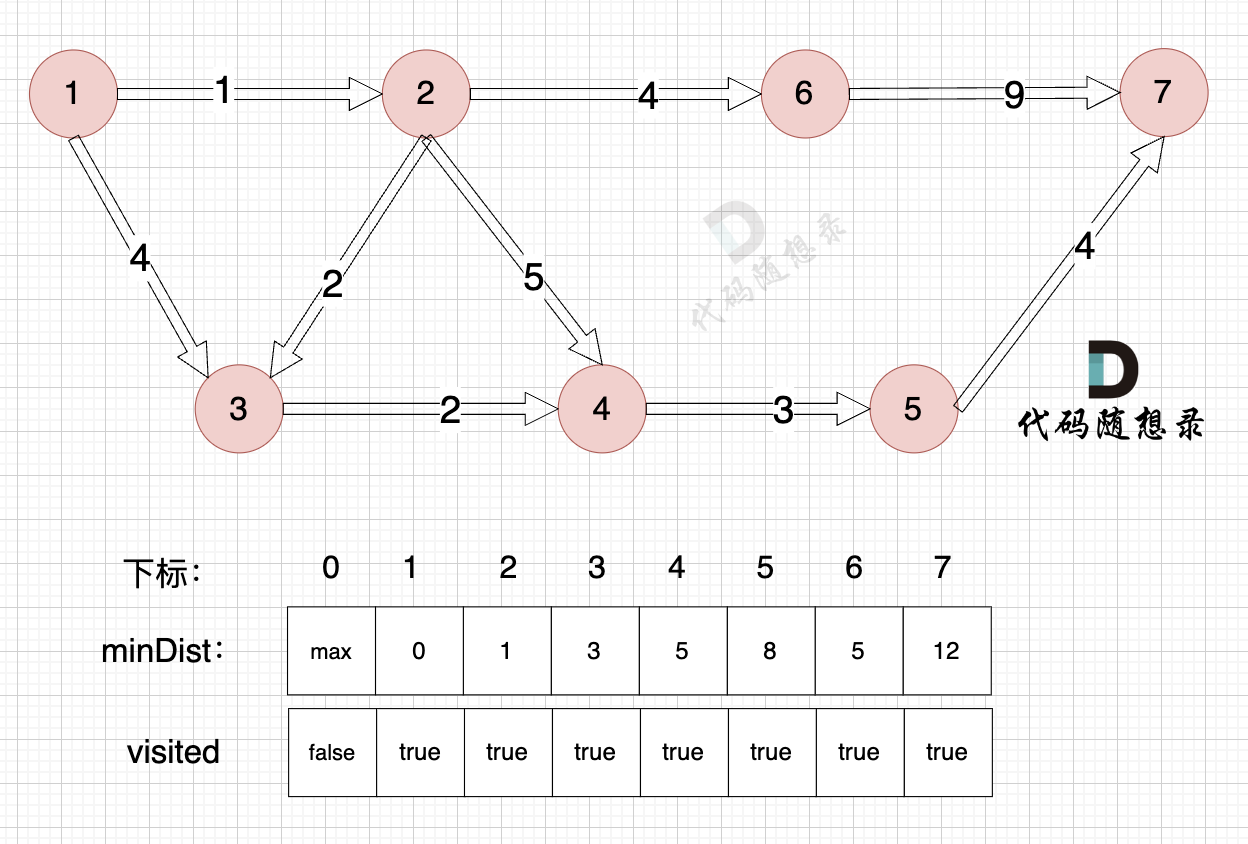
3、更新非訪問節點到源點的距離（即更新minDist數組），如圖：

節點7加入，但節點7到節點7的距離為0，所以不用更新minDist數組

最后我們要求起點（節點1）到終點（節點7）的距離。

再來回顧一下minDist數組的含義：記錄每一個節點距離源點的最小距離。

那么起到（節點1）到終點（節點7）的最短距離就是 minDist[7] ，按上面舉例講解來說，minDist[7] = 12，節點1 到節點7的最短路徑為 12。

路徑如圖：

在上面的講解中，每一步我都是按照 dijkstra 三部曲來講解的，理解了這三部曲，代碼也就好懂的。

#代碼實現

本題代碼如下，里面的三部曲我都做了注釋，大家按照我上面的講解來看如下代碼：

#include <iostream>
#include <vector>
#include <climits>
using namespace std;
int main() {
int n, m, p1, p2, val;
cin >> n >> m;vector<vector<int>> grid(n + 1, vector<int>(n + 1, INT_MAX));
for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
grid[p1][p2] = val;
}int start = 1;
int end = n;// 存儲從源點到每個節點的最短距離
std::vector<int> minDist(n + 1, INT_MAX);// 記錄頂點是否被訪問過
std::vector<bool> visited(n + 1, false);minDist[start] = 0;  // 起始點到自身的距離為0for (int i = 1; i <= n; i++) { // 遍歷所有節點int minVal = INT_MAX;
int cur = 1;// 1、選距離源點最近且未訪問過的節點
for (int v = 1; v <= n; ++v) {
if (!visited[v] && minDist[v] < minVal) {
minVal = minDist[v];
cur = v;
}
}visited[cur] = true;  // 2、標記該節點已被訪問// 3、第三步，更新非訪問節點到源點的距離（即更新minDist數組）
for (int v = 1; v <= n; v++) {
if (!visited[v] && grid[cur][v] != INT_MAX && minDist[cur] + grid[cur][v] < minDist[v]) {
minDist[v] = minDist[cur] + grid[cur][v];
}
}}if (minDist[end] == INT_MAX) cout << -1 << endl; // 不能到達終點
else cout << minDist[end] << endl; // 到達終點最短路徑}

時間復雜度：O(n^2)
空間復雜度：O(n^2)

#debug方法

寫這種題目難免會有各種各樣的問題，我們如何發現自己的代碼是否有問題呢？

最好的方式就是打日志，本題的話，就是將 minDist 數組打印出來，就可以很明顯發現哪里出問題了。

每次選擇節點后，minDist數組的變化是否符合預期，是否和我上面講的邏輯是對應的。

例如本題，如果想debug的話，打印日志可以這樣寫：

#include <iostream>
#include <vector>
#include <climits>
using namespace std;
int main() {
int n, m, p1, p2, val;
cin >> n >> m;vector<vector<int>> grid(n + 1, vector<int>(n + 1, INT_MAX));
for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
grid[p1][p2] = val;
}int start = 1;
int end = n;std::vector<int> minDist(n + 1, INT_MAX);std::vector<bool> visited(n + 1, false);minDist[start] = 0;
for (int i = 1; i <= n; i++) {int minVal = INT_MAX;
int cur = 1;for (int v = 1; v <= n; ++v) {
if (!visited[v] && minDist[v] < minVal) {
minVal = minDist[v];
cur = v;
}
}visited[cur] = true;for (int v = 1; v <= n; v++) {
if (!visited[v] && grid[cur][v] != INT_MAX && minDist[cur] + grid[cur][v] < minDist[v]) {
minDist[v] = minDist[cur] + grid[cur][v];
}
}// 打印日志：
cout << "select:" << cur << endl;
for (int v = 1; v <= n; v++) cout <<  v << ":" << minDist[v] << " ";
cout << endl << endl;;}
if (minDist[end] == INT_MAX) cout << -1 << endl;
else cout << minDist[end] << endl;}

打印后的結果：

select:1
1:0 2:1 3:4 4:2147483647 5:2147483647 6:2147483647 7:2147483647select:2
1:0 2:1 3:3 4:6 5:2147483647 6:5 7:2147483647select:3
1:0 2:1 3:3 4:5 5:2147483647 6:5 7:2147483647select:4
1:0 2:1 3:3 4:5 5:8 6:5 7:2147483647select:6
1:0 2:1 3:3 4:5 5:8 6:5 7:14select:5
1:0 2:1 3:3 4:5 5:8 6:5 7:12select:7
1:0 2:1 3:3 4:5 5:8 6:5 7:12

打印日志可以和上面我講解的過程進行對比，每一步的結果是完全對應的。

所以如果大家如果代碼有問題，打日志來debug是最好的方法

#如何求路徑

如果題目要求把最短路的路徑打印出來，應該怎么辦呢？

這里還是有一些“坑”的，本題打印路徑和 prim 打印路徑是一樣的，我在 prim算法精講【拓展】中已經詳細講解了。

在這里就不再贅述。

打印路徑只需要添加幾行代碼，打印路徑的代碼我都加上的日志，如下：

#include <iostream>
#include <vector>
#include <climits>
using namespace std;
int main() {
int n, m, p1, p2, val;
cin >> n >> m;vector<vector<int>> grid(n + 1, vector<int>(n + 1, INT_MAX));
for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
grid[p1][p2] = val;
}int start = 1;
int end = n;std::vector<int> minDist(n + 1, INT_MAX);std::vector<bool> visited(n + 1, false);minDist[start] = 0; //加上初始化
vector<int> parent(n + 1, -1);for (int i = 1; i <= n; i++) {int minVal = INT_MAX;
int cur = 1;for (int v = 1; v <= n; ++v) {
if (!visited[v] && minDist[v] < minVal) {
minVal = minDist[v];
cur = v;
}
}visited[cur] = true;for (int v = 1; v <= n; v++) {
if (!visited[v] && grid[cur][v] != INT_MAX && minDist[cur] + grid[cur][v] < minDist[v]) {
minDist[v] = minDist[cur] + grid[cur][v];
parent[v] = cur; // 記錄邊
}
}}// 輸出最短情況
for (int i = 1; i <= n; i++) {
cout << parent[i] << "->" << i << endl;
}
}

打印結果：

-1->1
1->2
2->3
3->4
4->5
2->6
5->7

對應如圖：

#出現負數

如果圖中邊的權值為負數，dijkstra 還合適嗎？

看一下這個圖：（有負權值）

節點1 到節點5 的最短路徑應該是節點1 -> 節點2 -> 節點3 -> 節點4 -> 節點5

那我們來看dijkstra 求解的路徑是什么樣的，繼續dijkstra 三部曲來模擬：（dijkstra模擬過程上面已經詳細講過，以下只模擬重要過程，例如如何初始化就省略講解了）

初始化：

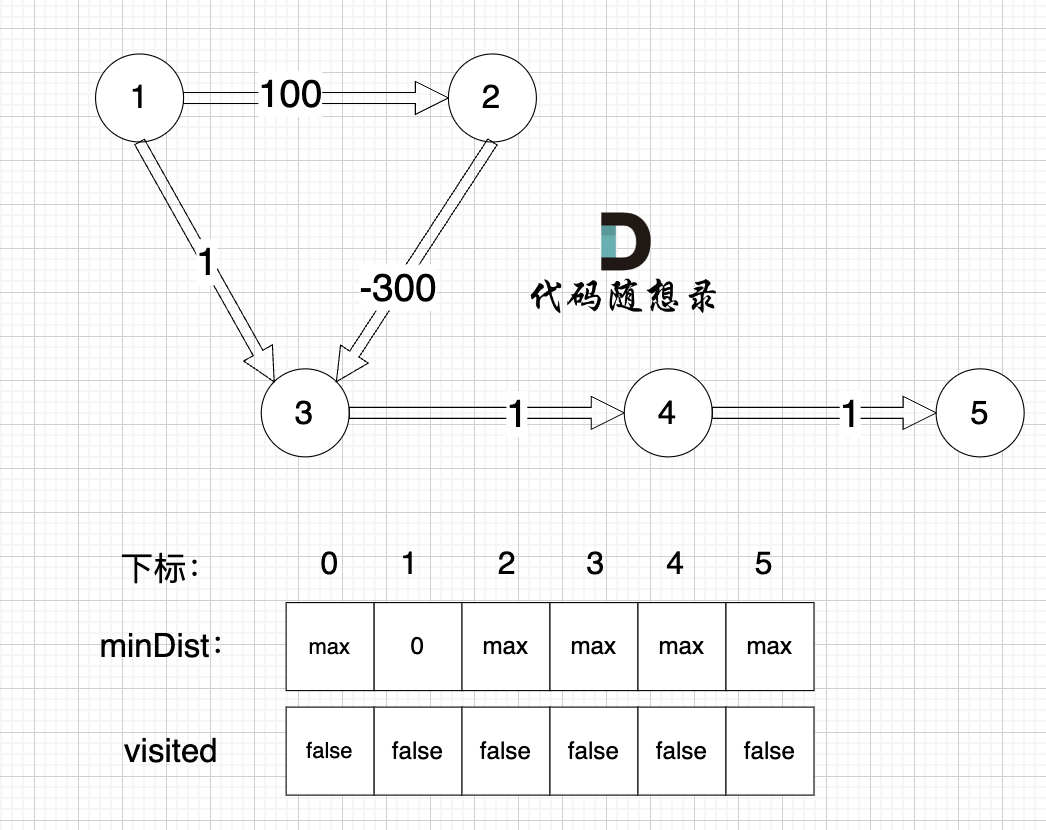1、選源點到哪個節點近且該節點未被訪問過

源點距離源點最近，距離為0，且未被訪問。

2、該最近節點被標記訪問過

標記源點訪問過

3、更新非訪問節點到源點的距離（即更新minDist數組），如圖：

更新 minDist數組，即：源點（節點1）到節點2 和節點3的距離。

源點到節點2的最短距離為100，小于原minDist[2]的數值max，更新minDist[2] = 100
源點到節點3的最短距離為1，小于原minDist[3]的數值max，更新minDist[4] = 1

1、選源點到哪個節點近且該節點未被訪問過

源點距離節點3最近，距離為1，且未被訪問。

2、該最近節點被標記訪問過

標記節點3訪問過

3、更新非訪問節點到源點的距離（即更新minDist數組），如圖：

由于節點3的加入，那么源點可以有新的路徑鏈接到節點4 所以更新minDist數組：

源點到節點4的最短距離為2，小于原minDist[4]的數值max，更新minDist[4] = 2

1、選源點到哪個節點近且該節點未被訪問過

源點距離節點4最近，距離為2，且未被訪問。

2、該最近節點被標記訪問過

標記節點4訪問過

3、更新非訪問節點到源點的距離（即更新minDist數組），如圖：

由于節點4的加入，那么源點可以有新的路徑鏈接到節點5 所以更新minDist數組：

源點到節點5的最短距離為3，小于原minDist[5]的數值max，更新minDist[5] = 5

1、選源點到哪個節點近且該節點未被訪問過

源點距離節點5最近，距離為3，且未被訪問。

2、該最近節點被標記訪問過

標記節點5訪問過

3、更新非訪問節點到源點的距離（即更新minDist數組），如圖：

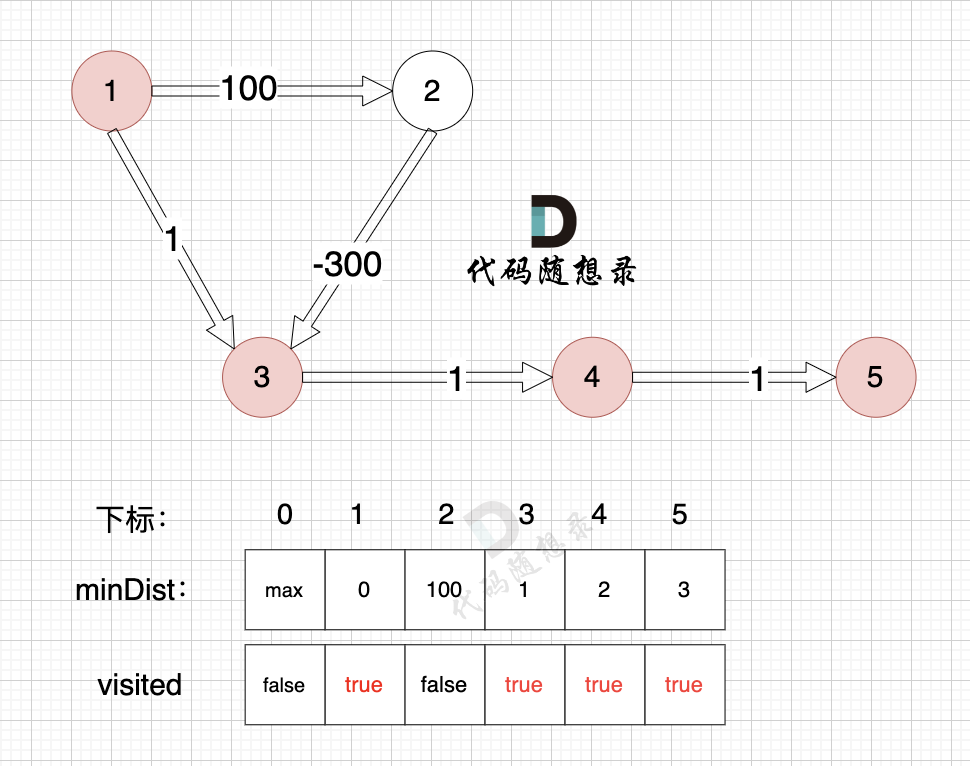節點5的加入，而節點5 沒有鏈接其他節點，所以不用更新minDist數組，僅標記節點5被訪問過了

1、選源點到哪個節點近且該節點未被訪問過

源點距離節點2最近，距離為100，且未被訪問。

2、該最近節點被標記訪問過

標記節點2訪問過

3、更新非訪問節點到源點的距離（即更新minDist數組），如圖：

至此dijkstra的模擬過程就結束了，根據最后的minDist數組，我們求節點1 到節點5 的最短路徑的權值總和為 3，路徑：節點1 -> 節點3 -> 節點4 -> 節點5

通過以上的過程模擬，我們可以發現之所以沒有走有負權值的最短路徑是因為在訪問節點 2 的時候，節點 3 已經訪問過了，就不會再更新了。

那有錄友可能會想：我可以改代碼邏輯啊，訪問過的節點，也讓它繼續訪問不就好了？

那么訪問過的節點還能繼續訪問會不會有死循環的出現呢？控制邏輯不讓其死循環？那特殊情況自己能都想清楚嗎？（可以試試，實踐出真知）

對于負權值的出現，大家可以針對某一個場景不斷去修改 dijkstra 的代碼，但最終會發現只是拆了東墻補西墻，對dijkstra的補充邏輯只能滿足某特定場景最短路求解。

對于求解帶有負權值的最短路問題，可以使用 Bellman-Ford 算法，我在后序會詳細講解。

#dijkstra與prim算法的區別

這里再次提示，需要先看我的 prim算法精講，否則可能不知道我下面講的是什么。

大家可以發現 dijkstra的代碼看上去怎么和 prim算法這么像呢。

其實代碼大體不差，唯一區別在三部曲中的第三步：更新minDist數組

因為prim是求非訪問節點到最小生成樹的最小距離，而 dijkstra是求非訪問節點到源點的最小距離。

prim 更新 minDist數組的寫法：

for (int j = 1; j <= v; j++) {
if (!isInTree[j] && grid[cur][j] < minDist[j]) {
minDist[j] = grid[cur][j];
}
}

因為 minDist表示節點到最小生成樹的最小距離，所以新節點cur的加入，只需要使用 grid[cur][j] ，grid[cur][j] 就表示 cur 加入生成樹后，生成樹到節點j 的距離。

dijkstra 更新 minDist數組的寫法：

for (int v = 1; v <= n; v++) {
if (!visited[v] && grid[cur][v] != INT_MAX && minDist[cur] + grid[cur][v] < minDist[v]) {
minDist[v] = minDist[cur] + grid[cur][v];
}
}

因為 minDist表示節點到源點的最小距離，所以新節點 cur 的加入，需要使用源點到cur的距離（minDist[cur]） + cur 到節點 v 的距離（grid[cur][v]），才是源點到節點v的距離。

此時大家可能不禁要想 prim算法可以有負權值嗎？

當然可以！

錄友們可以自己思考思考一下，這是為什么？

這里我提示一下：prim算法只需要將節點以最小權值和鏈接在一起，不涉及到單一路徑。

#總結

本篇，我們深入講解的dijkstra算法，詳細模擬其工作的流程。

這里我給出了 dijkstra 三部曲來幫助大家理解該算法，不至于每次寫 dijkstra 都是黑盒操作，沒有框架沒有章法。

在給出的代碼中，我也按照三部曲的邏輯來給大家注釋，只要理解這三部曲，即使過段時間對 dijkstra 算法有些遺忘，依然可以寫出一個框架出來，然后再去調試細節。

對于圖論算法，一般代碼都比較長，很難寫出代碼直接可以提交通過，都需要一個debug的過程，所以 學習如何debug 非常重要！

這也是我為什么在本文中單獨用來講解 debug方法。

本題求的是最短路徑和是多少，同時我們也要掌握如何把最短路徑打印出來。

我還寫了大篇幅來講解負權值的情況，只有畫圖帶大家一步一步去看出現負權值 dijkstra的求解過程，才能幫助大家理解，問題出在哪里。

如果我直接講：是因為訪問過的節點不能再訪問，導致錯過真正的最短路，我相信大家都不知道我在說啥。

最后我還講解了 dijkstra 和 prim 算法的相同與不同之處，我在圖論的講解安排中先講 prim算法再講 dijkstra 是有目的的， 理解這兩個算法的相同與不同之處有助于大家學習的更深入。

而不是學了 dijkstra 就只看 dijkstra，算法之間都是有聯系的，多去思考算法之間的相互聯系，會幫助大家思考的更深入，掌握的更徹底。

本篇寫了這么長，我也只講解了樸素版dijkstra，關于堆優化dijkstra，我會在下一篇再來給大家詳細講解。

加油

dijkstra（堆優化版）精講

卡碼網：47. 參加科學大會(opens new window)

【題目描述】

小明是一位科學家，他需要參加一場重要的國際科學大會，以展示自己的最新研究成果。

小明希望能選擇一條花費時間最少的路線，以確保他能夠盡快到達目的地。

【輸入描述】

第一行包含兩個正整數，第一個正整數 N 表示一共有 N 個公共汽車站，第二個正整數 M 表示有 M 條公路。

接下來為 M 行，每行包括三個整數，S、E 和 V，代表了從 S 車站可以單向直達 E 車站，并且需要花費 V 單位的時間。

【輸出描述】

輸出一個整數，代表小明從起點到終點所花費的最小時間。

輸入示例

輸出示例：12

【提示信息】

能夠到達的情況：

如下圖所示，起始車站為 1 號車站，終點車站為 7 號車站，綠色路線為最短的路線，路線總長度為 12，則輸出 12。

不能到達的情況：

如下圖所示，當從起始車站不能到達終點車站時，則輸出 -1。

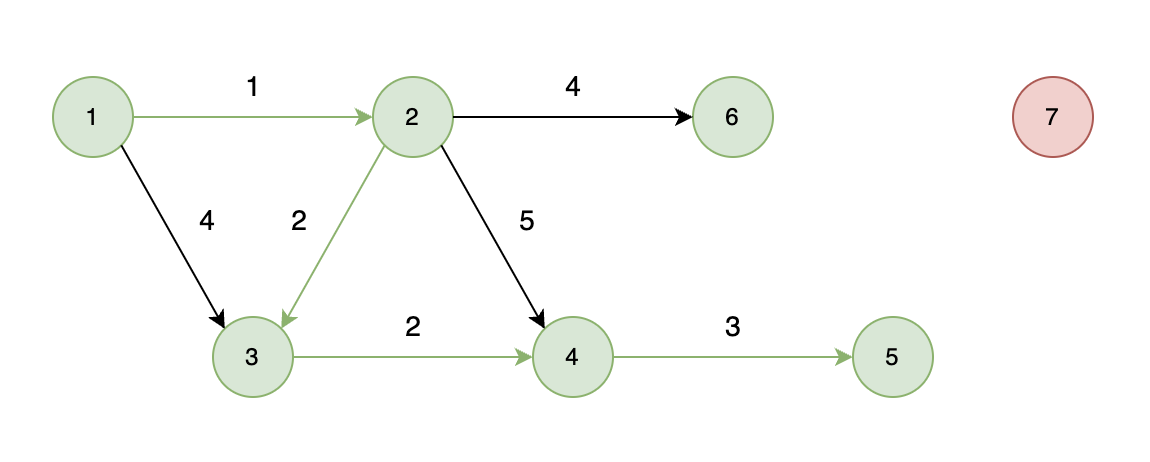數據范圍：

1 <= N <= 500; 1 <= M <= 5000;

#思路

本篇我們來講解堆優化版dijkstra，看本篇之前，一定要先看我講解的樸素版dijkstra，否則本篇會有部分內容看不懂。

在上一篇中，我們講解了樸素版的dijkstra，該解法的時間復雜度為 O(n^2)，可以看出時間復雜度只和 n （節點數量）有關系。

如果n很大的話，我們可以換一個角度來優先性能。

在講解最小生成樹的時候，我們講了兩個算法，prim算法（從點的角度來求最小生成樹）、Kruskal算法（從邊的角度來求最小生成樹）

這么在n 很大的時候，也有另一個思考維度，即：從邊的數量出發。

當 n 很大，邊的數量也很多的時候（稠密圖），那么上述解法沒問題。

但 n 很大，邊的數量很小的時候（稀疏圖），是不是可以換成從邊的角度來求最短路呢？

畢竟邊的數量少。

有的錄友可能會想，n （節點數量）很大，邊不就多嗎？怎么會邊的數量少呢？

別忘了，誰也沒有規定節點之間一定要有邊連接著，例如有一萬個節點，只有一條邊，這也是一張圖。

了解背景之后，再來看解法思路。

#圖的存儲

首先是圖的存儲。

關于圖的存儲主流有兩種方式：鄰接矩陣和鄰接表

#鄰接矩陣

鄰接矩陣使用二維數組來表示圖結構。鄰接矩陣是從節點的角度來表示圖，有多少節點就申請多大的二維數組。

例如： grid[2][5] = 6，表示節點 2 鏈接節點5 為有向圖，節點2 指向節點5，邊的權值為6 （套在題意里，可能是距離為6 或者消耗為6 等等）

如果想表示無向圖，即：grid[2][5] = 6，grid[5][2] = 6，表示節點2 與節點5 相互連通，權值為6。

如圖：

在一個 n （節點數）為8 的圖中，就需要申請 8 * 8 這么大的空間，有一條雙向邊，即：grid[2][5] = 6，grid[5][2] = 6

這種表達方式（鄰接矩陣）在邊少，節點多的情況下，會導致申請過大的二維數組，造成空間浪費。

而且在尋找節點鏈接情況的時候，需要遍歷整個矩陣，即 n * n 的時間復雜度，同樣造成時間浪費。

鄰接矩陣的優點：

表達方式簡單，易于理解
檢查任意兩個頂點間是否存在邊的操作非常快
適合稠密圖，在邊數接近頂點數平方的圖中，鄰接矩陣是一種空間效率較高的表示方法。

缺點：

遇到稀疏圖，會導致申請過大的二維數組造成空間浪費且遍歷邊的時候需要遍歷整個n * n矩陣，造成時間浪費

#鄰接表

鄰接表使用數組 + 鏈表的方式來表示。鄰接表是從邊的數量來表示圖，有多少邊才會申請對應大小的鏈表。

鄰接表的構造如圖：

這里表達的圖是：

節點1 指向節點3 和節點5
節點2 指向節點4、節點3、節點5
節點3 指向節點4，節點4指向節點1。

有多少邊鄰接表才會申請多少個對應的鏈表節點。

從圖中可以直觀看出使用數組 + 鏈表來表達邊的鏈接情況。

鄰接表的優點：

對于稀疏圖的存儲，只需要存儲邊，空間利用率高
遍歷節點鏈接情況相對容易

缺點：

檢查任意兩個節點間是否存在邊，效率相對低，需要 O(V)時間，V表示某節點鏈接其他節點的數量。
實現相對復雜，不易理解

#本題圖的存儲

接下來我們繼續按照稀疏圖的角度來分析本題。

在第一個版本的實現思路中，我們提到了三部曲：

第一步，選源點到哪個節點近且該節點未被訪問過
第二步，該最近節點被標記訪問過
第三步，更新非訪問節點到源點的距離（即更新minDist數組）

在第一個版本的代碼中，這三部曲是套在一個 for 循環里，為什么？

因為我們是從節點的角度來解決問題。

三部曲中第一步（選源點到哪個節點近且該節點未被訪問過），這個操作本身需要for循環遍歷 minDist 來尋找最近的節點。

同時我們需要遍歷所有未訪問過的節點，所以我們從節點角度出發，代碼會有兩層for循環，代碼是這樣的：（注意代碼中的注釋，標記兩層for循環的用處）


for (int i = 1; i <= n; i++) { // 遍歷所有節點，第一層for循環 int minVal = INT_MAX;
int cur = 1;// 1、選距離源點最近且未訪問過的節點 ， 第二層for循環
for (int v = 1; v <= n; ++v) {
if (!visited[v] && minDist[v] < minVal) {
minVal = minDist[v];
cur = v;
}
}visited[cur] = true;  // 2、標記該節點已被訪問// 3、第三步，更新非訪問節點到源點的距離（即更新minDist數組）
for (int v = 1; v <= n; v++) {
if (!visited[v] && grid[cur][v] != INT_MAX && minDist[cur] + grid[cur][v] < minDist[v]) {
minDist[v] = minDist[cur] + grid[cur][v];
}
}}

那么當從邊的角度出發，在處理三部曲里的第一步（選源點到哪個節點近且該節點未被訪問過）的時候，我們可以不用去遍歷所有節點了。

而且直接把邊（帶權值）加入到小頂堆（利用堆來自動排序），那么每次我們從堆頂里取出邊自然就是距離源點最近的節點所在的邊。

這樣我們就不需要兩層for循環來尋找最近的節點了。

了解了大體思路，我們再來看代碼實現。

首先是如何使用鄰接表來表述圖結構，這是擺在很多錄友面前的第一個難題。

鄰接表用數組+鏈表來表示，代碼如下：（C++中 vector 為數組，list 為鏈表，定義了 n+1 這么大的數組空間）

vector<list<int>> grid(n + 1);

不少錄友，不知道如何定義的數據結構，怎么表示鄰接表的，我來給大家畫一個圖：

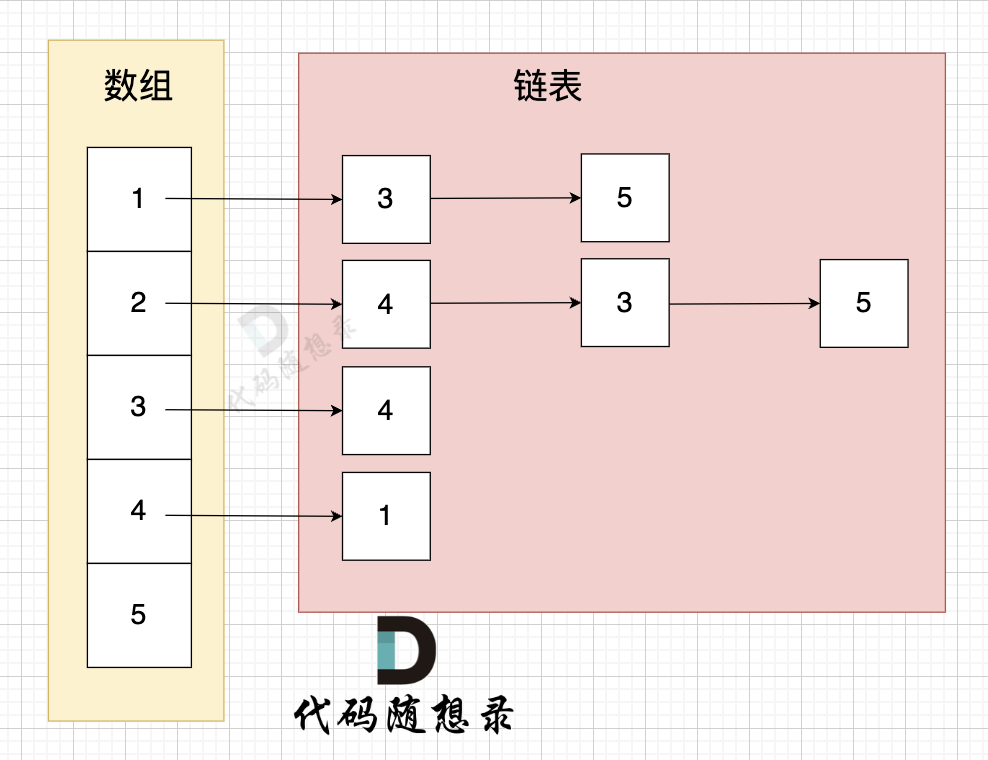圖中鄰接表表示：

節點1 指向節點3 和節點5
節點2 指向節點4、節點3、節點5
節點3 指向節點4
節點4 指向節點1

大家發現圖中的邊沒有權值，而本題中我們的邊是有權值的，權值怎么表示？在哪里表示？

所以在vector<list<int>> grid(n + 1);? 中就不能使用int了，而是需要一個鍵值對來存兩個數字，一個數表示節點，一個數表示指向該節點的這條邊的權值。

那么代碼可以改成這樣：（pair 為鍵值對，可以存放兩個int）

vector<list<pair<int,int>>> grid(n + 1);

舉例來給大家展示該代碼表達的數據如下：

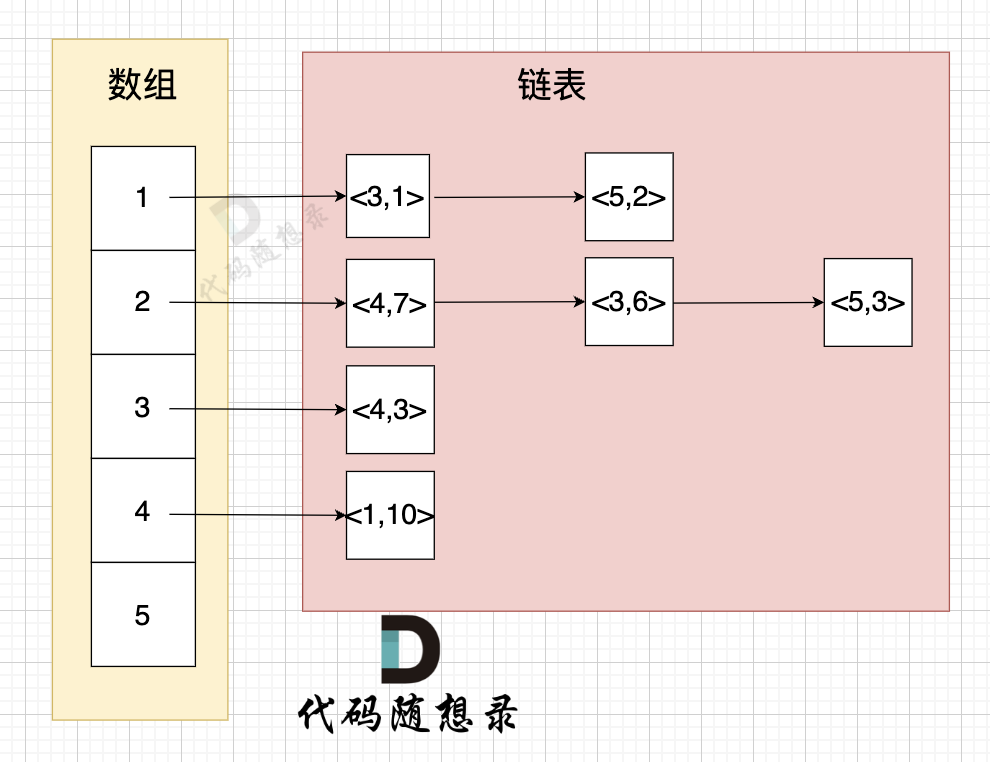節點1 指向節點3 權值為 1
節點1 指向節點5 權值為 2
節點2 指向節點4 權值為 7
節點2 指向節點3 權值為 6
節點2 指向節點5 權值為 3
節點3 指向節點4 權值為 3
節點5 指向節點1 權值為 10

這樣我們就把圖中權值表示出來了。

但是在代碼中使用 pair<int, int>? 很容易讓我們搞混了，第一個int 表示什么，第二個int表示什么，導致代碼可讀性很差，或者說別人看你的代碼看不懂。

那么可以定一個類來取代 pair<int, int>?

類（或者說是結構體）定義如下：

struct Edge {
int to;  // 鄰接頂點
int val; // 邊的權重Edge(int t, int w): to(t), val(w) {}  // 構造函數
};

這個類里有兩個成員變量，有對應的命名，這樣不容易搞混兩個int的含義。

所以本題中鄰接表的定義如下：

struct Edge {
int to;  // 鏈接的節點
int val; // 邊的權重Edge(int t, int w): to(t), val(w) {}  // 構造函數
};vector<list<Edge>> grid(n + 1); // 鄰接表

（我們在下面的講解中會直接使用這個鄰接表的代碼表示方式）

#堆優化細節

其實思路依然是 dijkstra 三部曲：

第一步，選源點到哪個節點近且該節點未被訪問過
第二步，該最近節點被標記訪問過
第三步，更新非訪問節點到源點的距離（即更新minDist數組）

只不過之前是通過遍歷節點來遍歷邊，通過兩層for循環來尋找距離源點最近節點。這次我們直接遍歷邊，且通過堆來對邊進行排序，達到直接選擇距離源點最近節點。

先來看一下針對這三部曲，如果用堆來優化。

那么三部曲中的第一步（選源點到哪個節點近且該節點未被訪問過），我們如何選？

我們要選擇距離源點近的節點（即：該邊的權值最小），所以我們需要一個小頂堆來幫我們對邊的權值排序，每次從小頂堆堆頂取邊就是權值最小的邊。

C++定義小頂堆，可以用優先級隊列實現，代碼如下：

// 小頂堆
class mycomparison {
public:
bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs) {
return lhs.second > rhs.second;
}
};
// 優先隊列中存放 pair<節點編號，源點到該節點的權值> 
priority_queue<pair<int, int>, vector<pair<int, int>>, mycomparison> pq;

（pair<int, int>?中第二個int 為什么要存源點到該節點的權值，因為這個小頂堆需要按照權值來排序）

有了小頂堆自動對邊的權值排序，那我們只需要直接從堆里取堆頂元素（小頂堆中，最小的權值在上面），就可以取到離源點最近的節點了（未訪問過的節點，不會加到堆里進行排序）

所以三部曲中的第一步，我們不用 for循環去遍歷，直接取堆頂元素：

// pair<節點編號，源點到該節點的權值>
pair<int, int> cur = pq.top(); pq.pop();

第二步（該最近節點被標記訪問過）這個就是將節點做訪問標記，和樸素dijkstra 一樣，代碼如下：

// 2. 第二步，該最近節點被標記訪問過
visited[cur.first] = true;

（cur.first? 是指取 pair<int, int>? 里的第一個int，即節點編號）

第三步（更新非訪問節點到源點的距離），這里的思路也是和樸素dijkstra一樣的。

但很多錄友對這里是最懵的，主要是因為兩點：

沒有理解透徹 dijkstra 的思路
沒有理解鄰接表的表達方式

我們來回顧一下樸素dijkstra 在這一步的代碼和思路（如果沒看過我講解的樸素版dijkstra，這里會看不懂）


// 3、第三步，更新非訪問節點到源點的距離（即更新minDist數組）
for (int v = 1; v <= n; v++) {
if (!visited[v] && grid[cur][v] != INT_MAX && minDist[cur] + grid[cur][v] < minDist[v]) {
minDist[v] = minDist[cur] + grid[cur][v];
}
}

其中 for循環是用來做什么的？是為了找到節點cur 鏈接指向了哪些節點，因為使用鄰接矩陣的表達方式所以把所有節點遍歷一遍。

而在鄰接表中，我們可以以相對高效的方式知道一個節點鏈接指向哪些節點。

再回顧一下鄰接表的構造（數組 + 鏈表）：

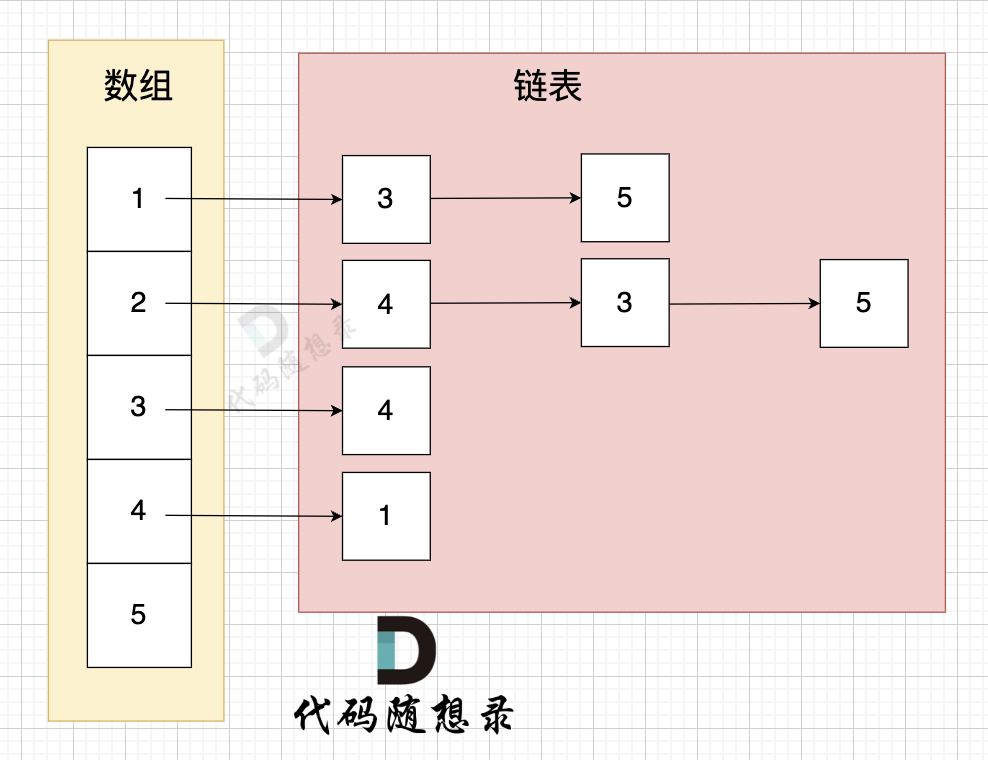假如加入的cur 是節點 2，那么 grid[2] 表示的就是圖中第二行鏈表。（grid數組的構造我們在上面「圖的存儲」中講過）

所以在鄰接表中，我們要獲取節點cur 鏈接指向哪些節點，就是遍歷 grid[cur節點編號] 這個鏈表。

這個遍歷方式，C++代碼如下：

for (Edge edge : grid[cur.first])

（如果不知道 Edge 是什么，看上面「圖的存儲」中鄰接表的講解）

?cur.first? 就是cur節點編號，參考上面pair的定義： pair<節點編號，源點到該節點的權值>

接下來就是更新非訪問節點到源點的距離，代碼實現和樸素dijkstra 是一樣的，代碼如下：

// 3. 第三步，更新非訪問節點到源點的距離（即更新minDist數組）
for (Edge edge : grid[cur.first]) { // 遍歷 cur指向的節點，cur指向的節點為 edge
// cur指向的節點edge.to，這條邊的權值為 edge.val
if (!visited[edge.to] && minDist[cur.first] + edge.val < minDist[edge.to]) { // 更新minDist
minDist[edge.to] = minDist[cur.first] + edge.val;
pq.push(pair<int, int>(edge.to, minDist[edge.to]));
}
}

但為什么思路一樣，有的錄友能寫出樸素dijkstra，但堆優化這里的邏輯就是寫不出來呢？

主要就是因為對鄰接表的表達方式不熟悉！

以上代碼中，cur 鏈接指向的節點編號為 edge.to，這條邊的權值為 edge.val ，如果對這里模糊的就再回顧一下 Edge的定義：

struct Edge {
int to;  // 鄰接頂點
int val; // 邊的權重Edge(int t, int w): to(t), val(w) {}  // 構造函數
};

確定該節點沒有被訪問過，!visited[edge.to]? ，目前源點到cur.first的最短距離（minDist） + cur.first 到 edge.to 的距離（edge.val）是否小于 minDist已經記錄的源點到 edge.to 的距離（minDist[edge.to]）

如果是的話，就開始更新操作。

即：

if (!visited[edge.to] && minDist[cur.first] + edge.val < minDist[edge.to]) { // 更新minDist
minDist[edge.to] = minDist[cur.first] + edge.val;
pq.push(pair<int, int>(edge.to, minDist[edge.to])); // 由于cur節點的加入，而新鏈接的邊，加入到優先級隊里中
}

同時，由于cur節點的加入，源點又有可以新鏈接到的邊，將這些邊加入到優先級隊里中。

以上代碼思路和樸素版dijkstra 是一樣一樣的，主要區別是兩點：

鄰接表的表示方式不同
使用優先級隊列（小頂堆）來對新鏈接的邊排序

#代碼實現

堆優化dijkstra完整代碼如下：

#include <iostream>
#include <vector>
#include <list>
#include <queue>
#include <climits>
using namespace std; 
// 小頂堆
class mycomparison {
public:
bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs) {
return lhs.second > rhs.second;
}
};
// 定義一個結構體來表示帶權重的邊
struct Edge {
int to;  // 鄰接頂點
int val; // 邊的權重Edge(int t, int w): to(t), val(w) {}  // 構造函數
};int main() {
int n, m, p1, p2, val;
cin >> n >> m;vector<list<Edge>> grid(n + 1);for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val; 
// p1 指向 p2，權值為 val
grid[p1].push_back(Edge(p2, val));}int start = 1;  // 起點
int end = n;    // 終點// 存儲從源點到每個節點的最短距離
std::vector<int> minDist(n + 1, INT_MAX);// 記錄頂點是否被訪問過
std::vector<bool> visited(n + 1, false); // 優先隊列中存放 pair<節點，源點到該節點的權值>
priority_queue<pair<int, int>, vector<pair<int, int>>, mycomparison> pq;// 初始化隊列，源點到源點的距離為0，所以初始為0
pq.push(pair<int, int>(start, 0)); minDist[start] = 0;  // 起始點到自身的距離為0while (!pq.empty()) {
// 1. 第一步，選源點到哪個節點近且該節點未被訪問過 （通過優先級隊列來實現）
// <節點， 源點到該節點的距離>
pair<int, int> cur = pq.top(); pq.pop();if (visited[cur.first]) continue;// 2. 第二步，該最近節點被標記訪問過
visited[cur.first] = true;// 3. 第三步，更新非訪問節點到源點的距離（即更新minDist數組）
for (Edge edge : grid[cur.first]) { // 遍歷 cur指向的節點，cur指向的節點為 edge
// cur指向的節點edge.to，這條邊的權值為 edge.val
if (!visited[edge.to] && minDist[cur.first] + edge.val < minDist[edge.to]) { // 更新minDist
minDist[edge.to] = minDist[cur.first] + edge.val;
pq.push(pair<int, int>(edge.to, minDist[edge.to]));
}
}}if (minDist[end] == INT_MAX) cout << -1 << endl; // 不能到達終點
else cout << minDist[end] << endl; // 到達終點最短路徑
}

時間復雜度：O(ElogE) E 為邊的數量
空間復雜度：O(N + E) N 為節點的數量

堆優化的時間復雜度只和邊的數量有關和節點數無關，在優先級隊列中放的也是邊。

以上代碼中，while (!pq.empty())? 里套了 for (Edge edge : grid[cur.first])?

?for? 里遍歷的是當前節點 cur 所連接邊。

那當前節點cur 所連接的邊也是不固定的，這就讓大家分不清，這時間復雜度究竟是多少？

其實 for (Edge edge : grid[cur.first])? 里最終的數據走向是給隊列里添加邊。

那么跳出局部代碼，整個隊列一定是所有邊添加了一次，同時也彈出了一次。

所以邊添加一次時間復雜度是 O(E)， while (!pq.empty())? 里每次都要彈出一個邊來進行操作，在優先級隊列（小頂堆）中彈出一個元素的時間復雜度是 O(logE) ，這是堆排序的時間復雜度。

（當然小頂堆里是添加元素的時候排序，還是取數元素的時候排序，這個無所謂，時間復雜度都是O(E)，總之是一定要排序的，而小頂堆里也不會滯留元素，有多少元素添加一定就有多少元素彈出）

所以該算法整體時間復雜度為 O（ElogE)

網上的不少分析會把 n （節點的數量）算進來，這個分析是有問題的，舉一個極端例子，在n 為 10000，且是有一條邊的圖里，以上代碼，大家感覺執行了多少次？

?while (!pq.empty())? 中的 pq 存的是邊，其實只執行了一次。

所以該算法時間復雜度和節點沒有關系。

至于空間復雜度，鄰接表是數組 + 鏈表數組的空間是 N ，有E條邊就申請對應多少個鏈表節點，所以是復雜度是 N + E

#拓展

當然也有錄友可能想堆優化dijkstra 中我為什么一定要用鄰接表呢，我就用鄰接矩陣行不行？

也行的。

但正是因為稀疏圖，所以我們使用堆優化的思路，如果我們還用鄰接矩陣去表達這個圖的話，就是 一個高效的算法使用了低效的數據結構，那么整體算法效率依然是低的。

如果還不清楚為什么要使用鄰接表，可以再看看上面我在「圖的存儲」標題下的講解。

這里我也給出鄰接矩陣版本的堆優化dijkstra代碼：

#include <iostream>
#include <vector>
#include <list>
#include <climits>
using namespace std;
// 小頂堆
class mycomparison {
public:
bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs) {
return lhs.second > rhs.second;
}
};int main() {
int n, m, p1, p2, val;
cin >> n >> m;vector<vector<int>> grid(n + 1, vector<int>(n + 1, INT_MAX));for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
// p1 指向 p2，權值為 val
grid[p1][p2] = val;
}int start = 1;  // 起點
int end = n;    // 終點// 存儲從源點到每個節點的最短距離
std::vector<int> minDist(n + 1, INT_MAX);// 記錄頂點是否被訪問過
std::vector<bool> visited(n + 1, false);// 優先隊列中存放 pair<節點，源點到該節點的距離>
priority_queue<pair<int, int>, vector<pair<int, int>>, mycomparison> pq;// 初始化隊列，源點到源點的距離為0，所以初始為0
pq.push(pair<int, int>(start, 0));minDist[start] = 0;  // 起始點到自身的距離為0while (!pq.empty()) {
// <節點， 源點到該節點的距離>
// 1、選距離源點最近且未訪問過的節點
pair<int, int> cur = pq.top(); pq.pop();if (visited[cur.first]) continue;visited[cur.first] = true; // 2、標記該節點已被訪問// 3、第三步，更新非訪問節點到源點的距離（即更新minDist數組）
for (int j = 1; j <= n; j++) {
if (!visited[j] && grid[cur.first][j] != INT_MAX && (minDist[cur.first] + grid[cur.first][j] < minDist[j])) {
minDist[j] = minDist[cur.first] + grid[cur.first][j];
pq.push(pair<int, int>(j, minDist[j]));
}
}
}if (minDist[end] == INT_MAX) cout << -1 << endl; // 不能到達終點
else cout << minDist[end] << endl; // 到達終點最短路徑}