點贊👍👍收藏🌟🌟關注💖💖
你的支持是對我最大的鼓勵，我們一起努力吧!😃😃

1.分治

分治思想就如同它的名字一樣：分而治之。

將一個大問題劃分成若干個相同或者相識的子問題。然后在將子問題在劃分成若干個相同或者相識的子問題，直到劃分到不能在劃分。然后解決子問題，子問題都解決完了，大問題也就被解決完了。快速排序和歸并排序就用的分治思想。

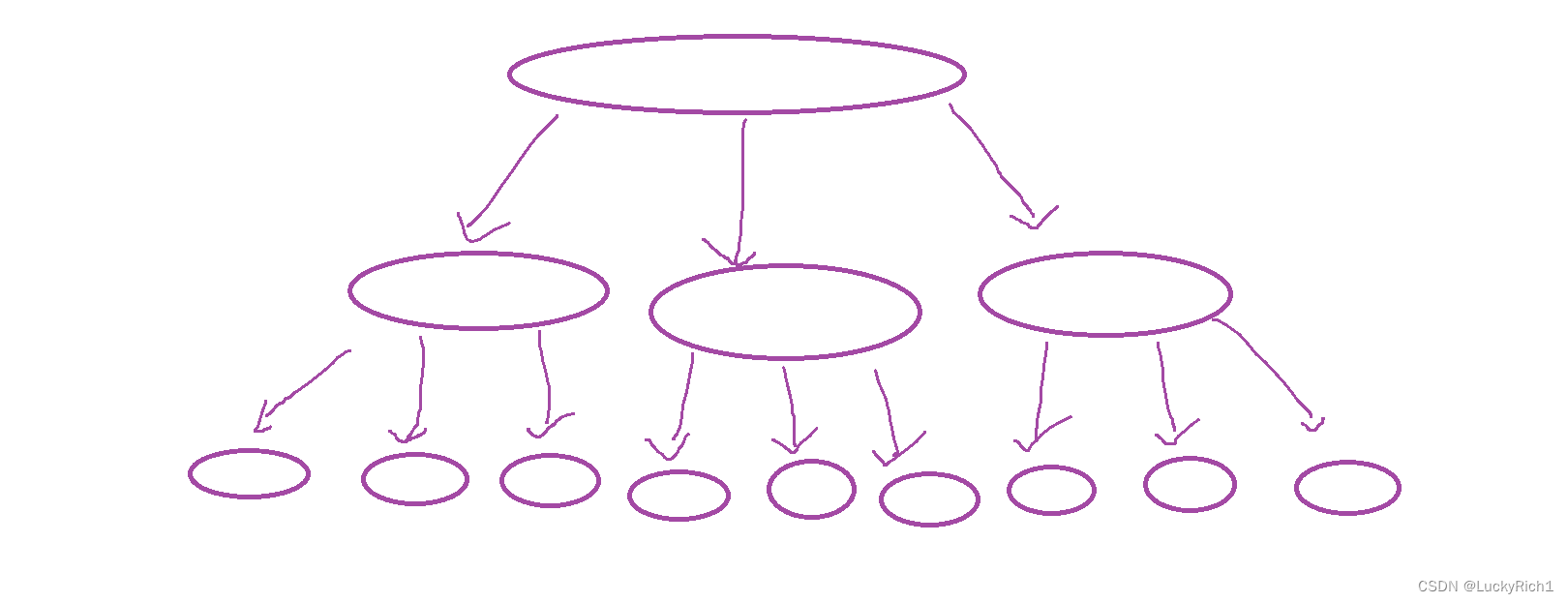
以前我們學快速排序是在數組中選擇一個基準元素，然后將數組分成左右兩個區間，左區間比基準元素小，右區間比基準元素大。然后遞歸的去左區間和有區間排序，這種做法是將數組分成了兩份。但是對于重復元素非常多的數組即使使用快速排序也會超時。因此這里我們學習新的劃分方法，將數組劃分成三份。

還是選一個基準元素將數組劃分成三份，左區間元素都比基準元素小。中間區間元素和基準元素相同，右區間元素都比基準元素大。因為中間都是等于key的一定就是在最終位置，所以接下來遞歸還是只考慮左區間和右區間。

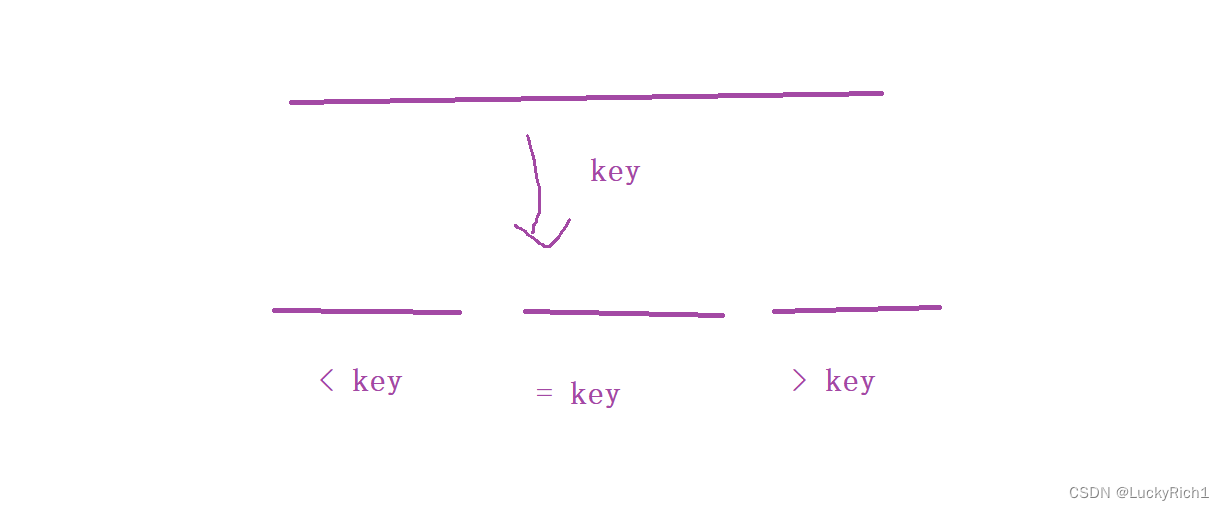
2.顏色分類

題目鏈接：75. 顏色分類

題目分析：

說起來這道題并不是真正的分治快速排序，而是把數組按照一定規則劃分成三塊的。當把這道題解決后，快排寫的就非常簡單。

這道題就相當于選擇一個基準元素1，把小于1的放左邊，大于1的放右邊，等于1的放中間。

算法原理：

雙指針可以將數組分成兩塊，具體怎么分，雙指針系列第一道題移動零。這里我們需要三個指針將數組分成三塊！

每個指針的作用：
i指針：遍歷整個數組
left：標記 0 區域的最右側
right：標記 2 區域的最左側

三個指針將數組分成4份：
[0，left] ：全都是0
[left+1，i-1]：全都是1
[i，right-1]：待掃描的元素
[rigth+1，n-1]：全都是2

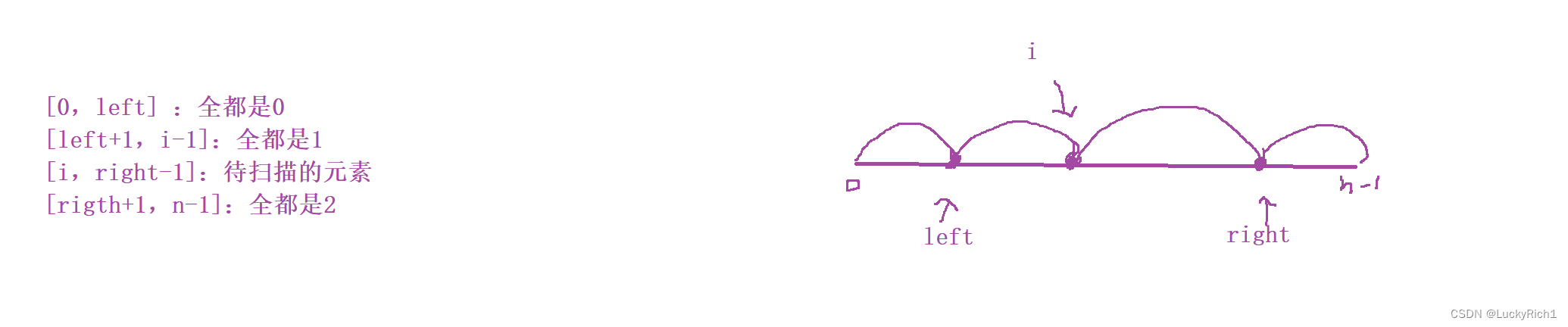
接下來就討論nums[i]是0或1或2應該怎么辦？

當nums[i]為0的時候，要把0加入到左邊區域，left指向的是 0 最右側區域，此時left+1，然后將 i 位置和 left+1 元素交換，然后i+1。

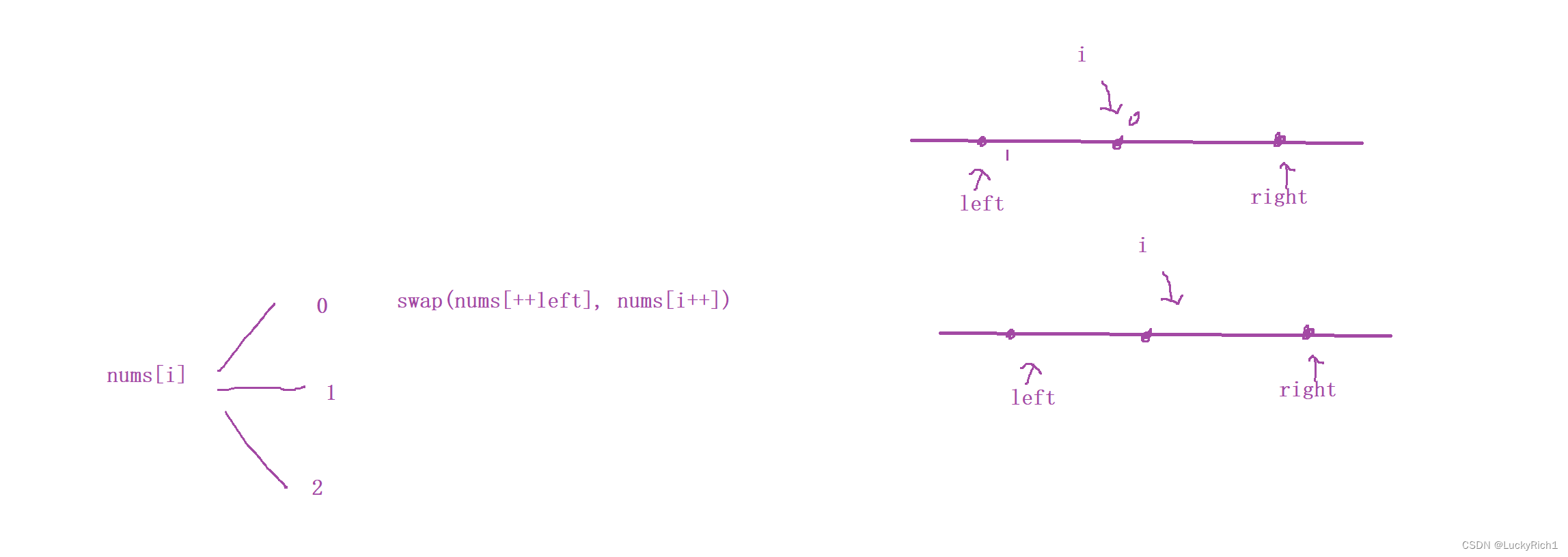
還有一種極端情況 i 就在 left+1的為位置，并且正好是0。但是這種處理方法和上面一樣。

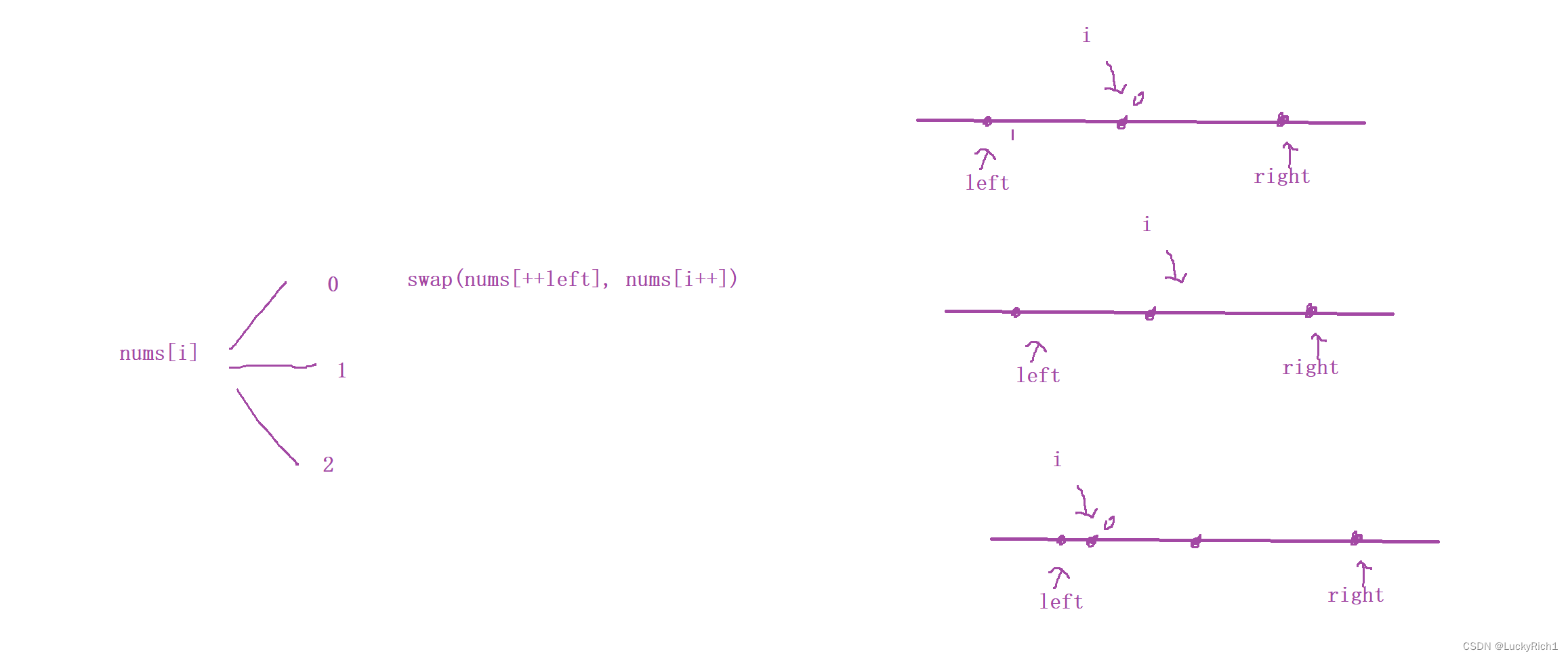
當nums[i]為1的時候，i 指針往后走就行了

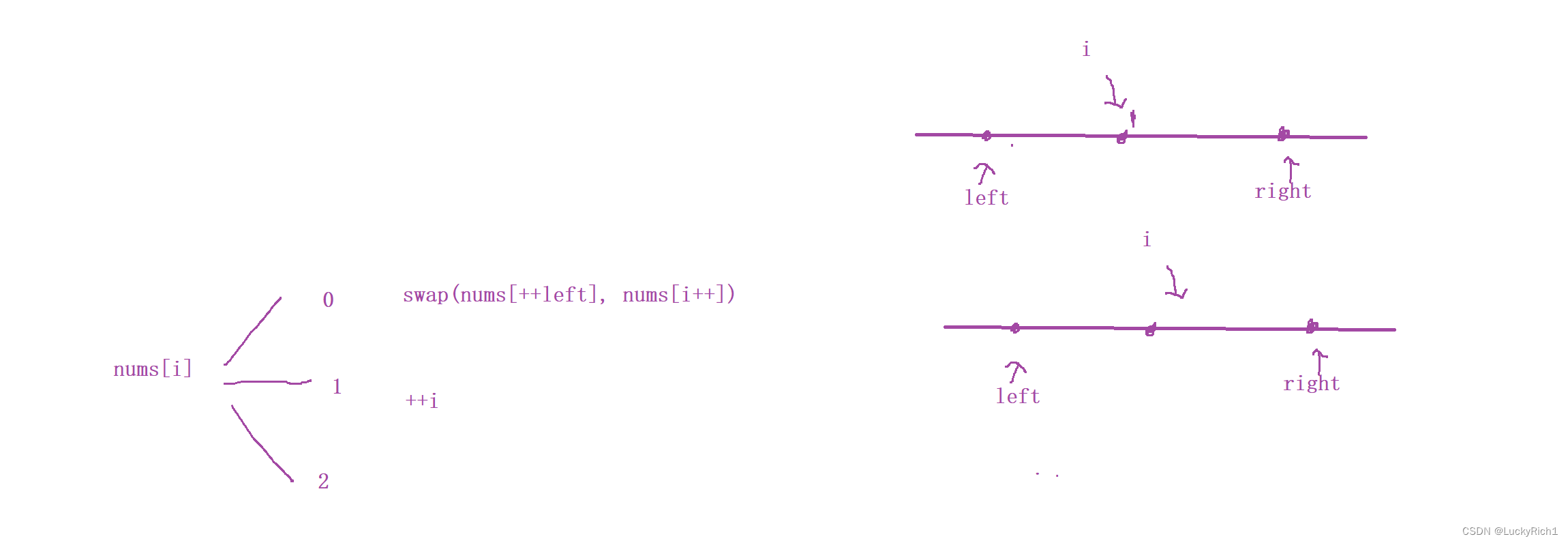
當nums[i]為2的時候，我們要將2加入到右邊區間，也就是加入到 right - 1 的位置。交換 i 位置和 right -1 位置的元素。但是此時需要注意的是 交換給 i 位置的元素是待掃描的元素，因此 i 指針不能往后走！

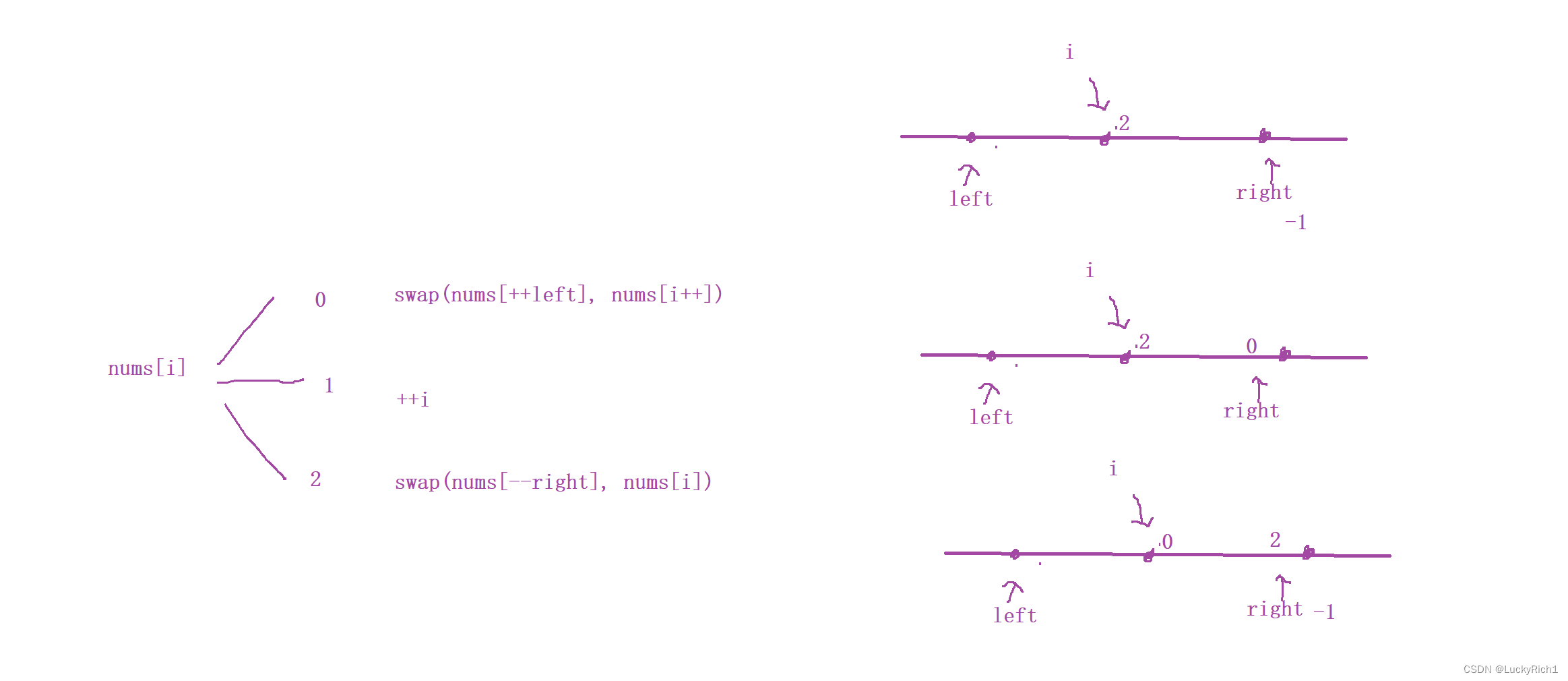
class Solution {
public:void sortColors(vector<int>& nums) {int n = nums.size();int i = 0, left = -1, right = n;while(i < right){if(nums[i] == 0)swap(nums[++left], nums[i++]);else if(nums[i] == 2)swap(nums[--right], nums[i]);else++i;}}
};

3.排序數組

題目鏈接：912. 排序數組

題目描述：

算法原理：

在數組中選擇一個基準元素key，根據key將數組分成左右區間，左區間元素小于等于key，右區間元素大于key。這個key就處于排序的最終位置。然后在將左區間排排序，右區間排排序，重復上述過程。整體就有序了。時間復雜度(nlogn)

但是如果數組都是重復元素，此時選擇基準元素間將數組分成左右兩區間就不行了。時間復雜度退化成O(n^2)

所以我們學習一個更優的做法，將 數組分三塊 思想來實現快速排序

我們先選一個基準元素key，將數組分成三塊。左區間小于key，中間區間等于key，右區間大于key。中間區間已經在排序后的最終位置，所以只用去去左區間排序，右區間排序。重復上述過程，整體就有序了。

數組如何分三塊和顏色分類一模一樣。定義一個i 指針 掃描數組，left指針 指向左區間小于key的最右側， right指針 指向右區間大于key的最左側。然后分情況討論就好了。

即使數組全部都是重復元素，我們經過一次數組劃分，整個數組都是中間區間，左右區間不存在，也不用在遞歸下去了，直接結束。時間復雜度O(n)

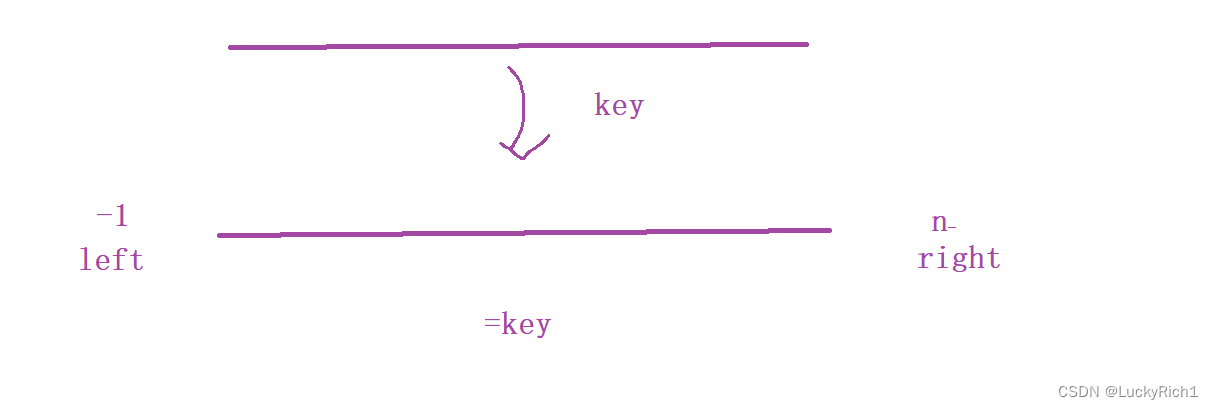
優化：用隨機的方式選擇基準元素
之前常用的三數取中，還是不夠隨機。要想時間復雜度逼近O(nlogn)就要用隨機的方式選擇基準元素。

隨機選擇就是讓數組中每個元素被選擇的概率相同，然后返回被選擇的元素。

使用產生隨機數的函數 rand()，讓生成的隨機數%這個區間的長度，然后加上left，這是在這個區間內的隨機數的下標，然后返回對應下標的元素。

class Solution {
public:vector<int> sortArray(vector<int>& nums) {srand((unsigned int)time(nullptr));QuickSort(nums,0,nums.size()-1);return nums;}void QuickSort(vector<int>& nums, int l, int r){if(l >= r) return;//數組分三塊int key = getRandom(nums, l ,r);int i = l, left = l - 1, right = r + 1;while(i < right){if(nums[i] < key)swap(nums[++left], nums[i++]);else if(nums[i] == key)++i;elseswap(nums[--right], nums[i]);}QuickSort(nums, l , left);QuickSort(nums, right, r);}int getRandom(vector<int>& nums, int left, int right){return nums[rand() % (right - left + 1) + left];}

4.數組中的第K個最大元素

題目鏈接：215. 數組中的第K個最大元素

題目分析：

給定整數數組 nums 和整數 k，請返回數組中第 k 個最大的元素。其實就是一個TopK問題。

TopK問題四種問法：

第 k 個最大的元素
第 k 個最小的元素
前 k 個最大的元素
前 k 個最小的元素

可以使用堆排序， 時間復雜度O(nlogn)

還有一種就是快速選擇算法，快速選擇算法是基于快排實現的。時間復雜度O(n)。

算法原理：

一定要把數組分三塊+隨機選擇基準元素掌握，才能懂這道題。

核心操作還是選擇一個基準元素key，將數組分成< key ， = key ，> key 三塊區域。在這道題中我們是要找到第K大元素，這個第K大元素有可能落在三個區域中的任何一個區域。如果有一種方法能夠確定第K大元素能夠落在那個區域，那另外兩個區域就不用考慮了。僅需在確定的區域里面遞歸找。所以說它是比快排更快的一種算法。

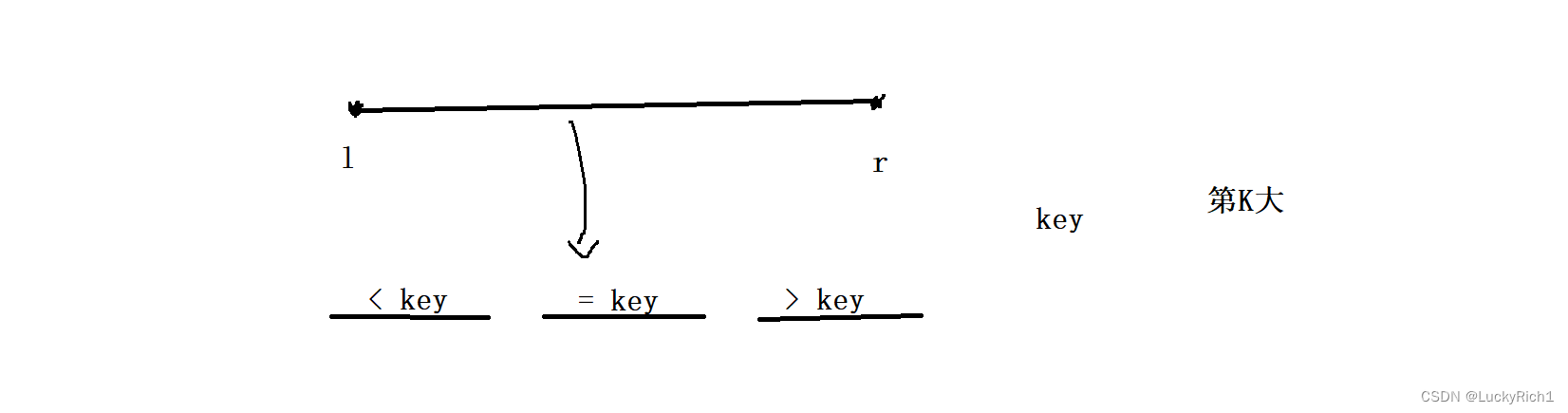
接下來重點就是如何確定第K大元素落在左邊區域、中間區域、還是右邊區域。
此時我們先統計出每個區域中元素的個數，假設左邊區域元素個數為 a，中間區域元素個數為 b，右邊區域元素個數為 c。

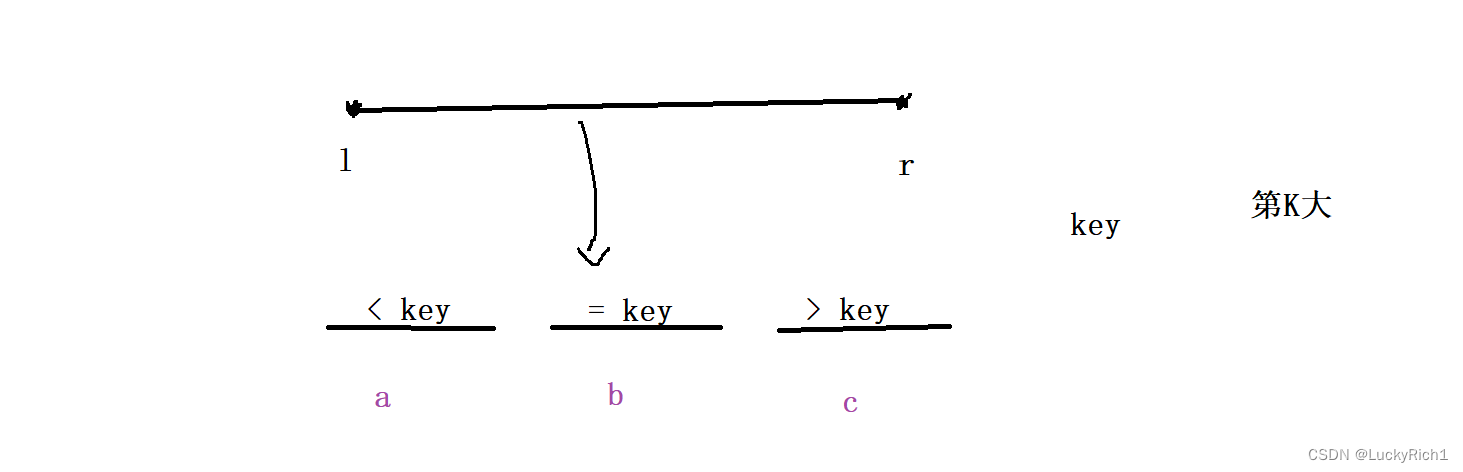
此時就分三種情況討論：

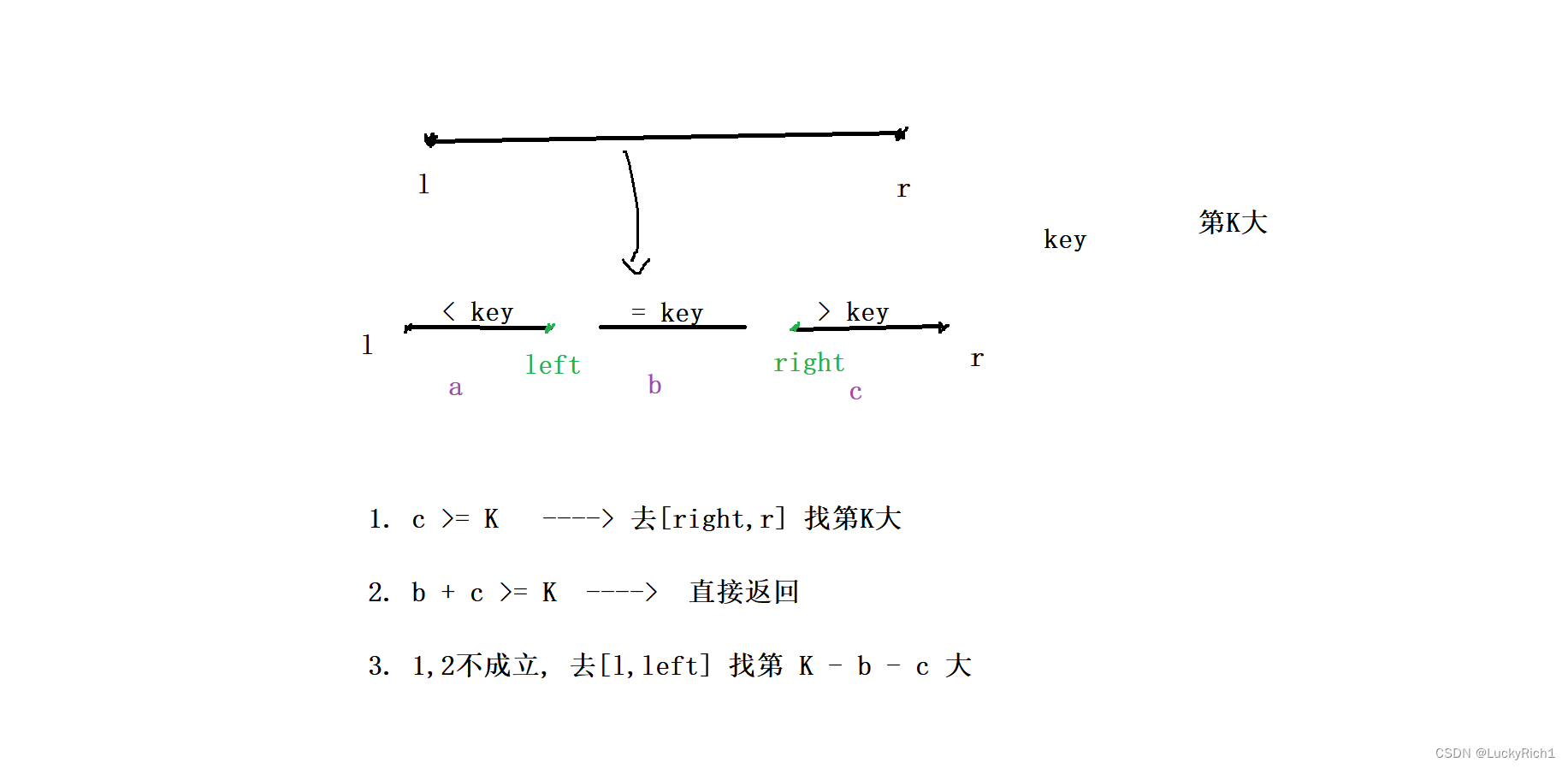
因為求第K大，所以可以先考慮右邊區域，因為右邊區域都是大元素聚集地，第K大最有可能在右邊區域。

1. 第一種情況：如果第K大是落在右邊區域，此時 c >= K，因為c表示大元素有多少個，而K表示找第K大的元素。如果 c >= K ，那第K大一定是落在右邊區域。此時我們僅需到[right，r]，找第K大。
2. 第二種情況：如果到了第二情況那第一種情況一定是不成立的。如果第K大是落在中間區域，此時 b + c >= K，又因為第一種情況不滿足，所有第K大一定是落在中間區域。此時就找到了也不用遞歸了。直接返回就可以。
3. 第三種情況：第一、第二種情況全部不成立，第K大一定落在左邊區域，去**[l，left]找**，但是此時并不是去找第K大了，本來是想在整個區間找第K大，但是第K大元素確定不在中間區域和右邊區域，中間和右邊區域都要被拋棄，此時去找左邊區間找的是第 K - b - c 大的元素

class Solution {
public:int findKthLargest(vector<int>& nums, int k) {srand((unsigned int)time(nullptr));return QuickSort(nums,0,nums.size()-1,k);}int QuickSort(vector<int>& nums, int l, int r, int k){//不用考慮區間不存在的情況,因為下面的判斷K落在那個區域,只要滿足進入的一定是有的if(l == r) return nums[l];// 1.隨機選擇基準元素int key = GetRandom(nums, l, r);// 2.根據基準元素將數組分三塊int i = l, left = l - 1, right = r + 1;while(i < right){if(nums[i] < key) swap(nums[++left], nums[i++]);else if(nums[i] == key) ++i;else swap(nums[--right], nums[i]);}//3.計算每個區間都有多少元素,然后選擇區間遞歸int b = right - 1 - left , c = r - right + 1; if(c >= k) return QuickSort(nums, right, r ,k);else if(b + c >= k) return key;else return QuickSort(nums, l, left, k - b - c);}int GetRandom(vector<int>& nums, int left, int right){return nums[rand() % (right - left + 1) + left];}// int findKthLargest(vector<int>& nums, int k) {//     //前k個建小堆//     priority_queue<int,vector<int>,greater<int>> pq(nums.begin(),nums.begin()+k);//     //N-k與堆頂元素比較，大于堆頂就入堆，再次調整成小堆//     for(size_t i=k;i<nums.size();++i)//     {//         if(nums[i]>pq.top())//         {//             pq.pop();//             pq.push(nums[i]);//         }//     }//     return pq.top();// }
};

5.庫存管理 III

題目鏈接：LCR 159. 庫存管理 III

題目分析：

實際上這也是一個TopK問題，讓找前K個最小元素。注意返回結果并不考慮順序問題。

算法原理：

解法一：排序 ，時間復雜度O(nlogn)
解法二：堆 ，時間復雜度O(nlogk)
解法三：快速選擇算法，時間復雜度O(n)

數組分三塊+隨機選擇基準元素。
選擇一個基準元素key，將數組分成< key ， = key ，> key 三塊區域。找前K個最小的元素，落在三個區域中任何一個。統計除每個區域元素個數，然后選擇去那個區域找。

分三種情況：
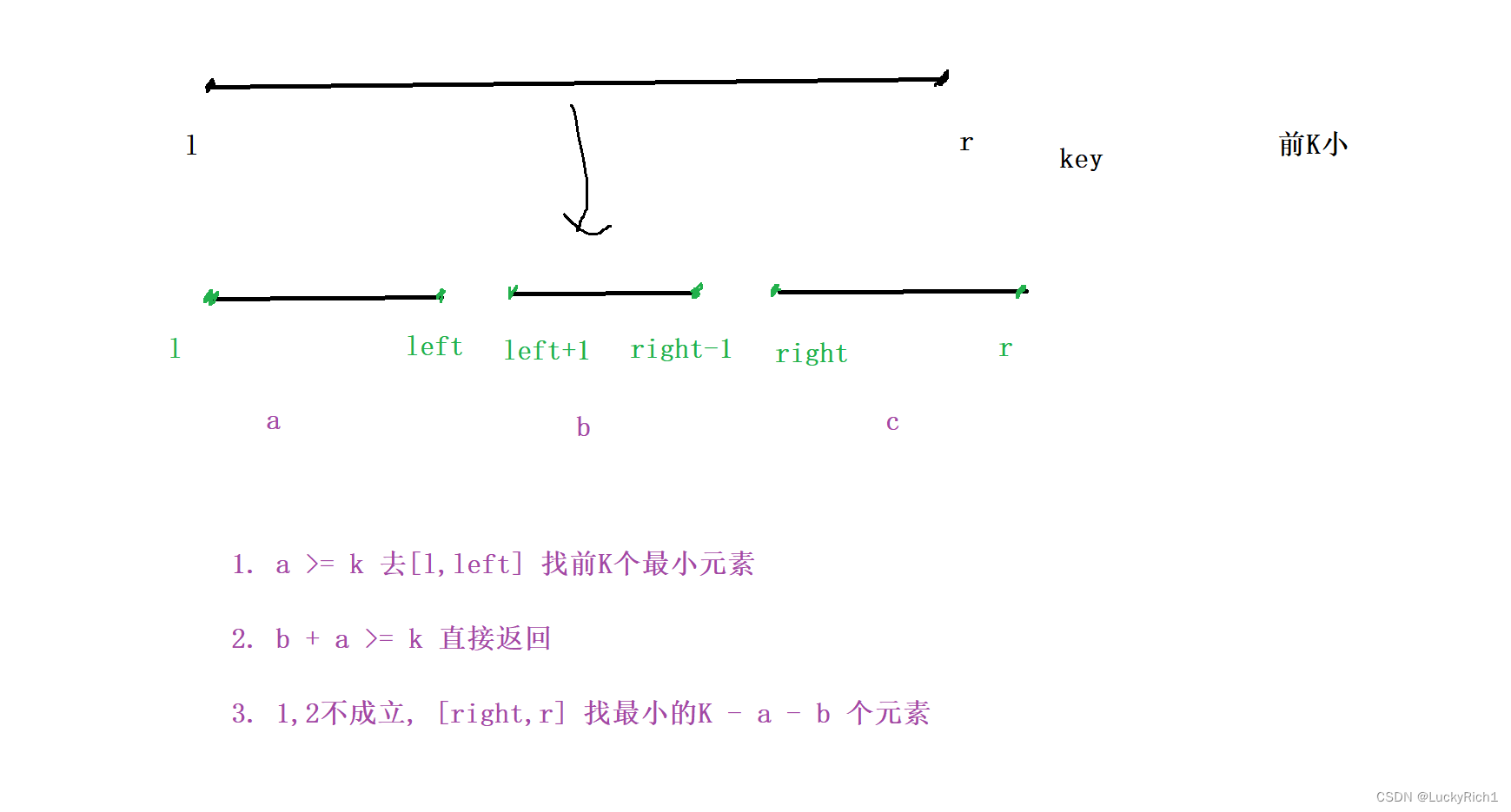
因為前K下最小元素最有可能出現在左邊區域，因此先判斷左邊區域

1. a >= K ，去[l，left] 找前K個最小元素
2. b + a >= K ，直接返回
3. 1、2都不成立，去[right，r] 找 K - a - b 個最小元素

class Solution {
public:vector<int> inventoryManagement(vector<int>& nums, int k) {srand((unsigned int)time(nullptr));QuickSort(nums, 0, nums.size() - 1, k);return {nums.begin(),nums.begin() + k};}void QuickSort(vector<int>& nums, int l, int r, int k){if(l >= r) return;// 1. 隨機選擇基準元素int key = GetRandom(nums, l, r);// 2. 數組分三塊int i = l, left = l - 1, right = r + 1;while(i < right){if(nums[i] < key) swap(nums[++left], nums[i++]);else if(nums[i] == key) ++i;else swap(nums[--right], nums[i]);}// 3. 分情況討論int a = left - l + 1, b = right - left - 1;if(a >= k) QuickSort(nums, l, left, k);else if(a + b >= k) return;else QuickSort(nums, right, r, k - a - b);}int GetRandom(vector<int>& nums, int left, int right){return nums[rand() % (right - left + 1) + left];}
};