1. 題目描述

題目中轉：69. x 的平方根

2.詳細題解

? ? 不能使用系統內置的函數，尋找某個數（假定為x）的算術平方根，并返回算術平方根的整數部分，最直觀的方法是從0依次開始嘗試所有小于等于x的數（假定為y），當y*y的積小于等于x時，繼續遍歷下一個數，直至y*y的積首次大于x時，此時y-1即為x的算術平方根的整數部分，如Python方法一逐個遍歷實現。
??上述方法遍歷的過程中，每次僅能排除判斷一個數字是否滿足，有沒有辦法一次性判斷或者排除多個數字呢？這就是二分查找算法，簡單的說，即待查數據需有序，每次判斷時折中取中間值進行對比，以判斷目標值可能存在的那一半，從而快速定位目標值，每次判斷可以排除一半的空間大小。具體算法如下：

• Step1：前置條件：個已排序的數組 arr 和待查找的元素 target。；
• Step2：初始化：兩個指針 left 和 right，分別指向數組的起始和結束位置；
• Step3：計算中間元素的索引： mid = (left + right) / 2；
• Step4：比較中間元素 arr[mid] 與 target；
• ?? 如果 arr[mid] == target，則找到目標值，返回 mid，程序結束；
• ?? 如果 arr[mid] < target，則目標值可能在 mid 的右側，更新 left = mid + 1；
• ?? 如果 arr[mid] > target，則目標值可能在 mid 的左側，更新 right = mid - 1；
• Step5：當 left <= right 時，循環執行Step3_Step4.

??對于此題，是計算算術平方根的整數部分，因此等價于尋找首次平方之和大于x的數，該數減1即為x的算術平方根（假定x的算術平方根為y.z,其中y為整數部分，z為小數部分，y*y的結果是小于x，而(y+1）*(y+1)是大于x的）。因此，針對此題，二分查找算法在返回值方面有一點點不同，應當返回最后的右指針指向的值，為什么呢？因為right為最后一次mid值大于x時減1的值，其它的mid值均小于x，故最后一次大于x的mid值減1即為目標整數，即right。實現詳見Python方法二和Java實現。

3.代碼實現

3.1 Python

方法一：逐個遍歷

class Solution:def mySqrt(self, x: int) -> int:left = 0while left * left <= x:left += 1return left-1

方法二：二分查找

class Solution:def mySqrt(self, x: int) -> int:left, right = 0, x//2while left <= right:mid = (left + right) // 2mul = mid * midif mul == x:return midelif mul < x:left = mid + 1else:right = mid - 1return right

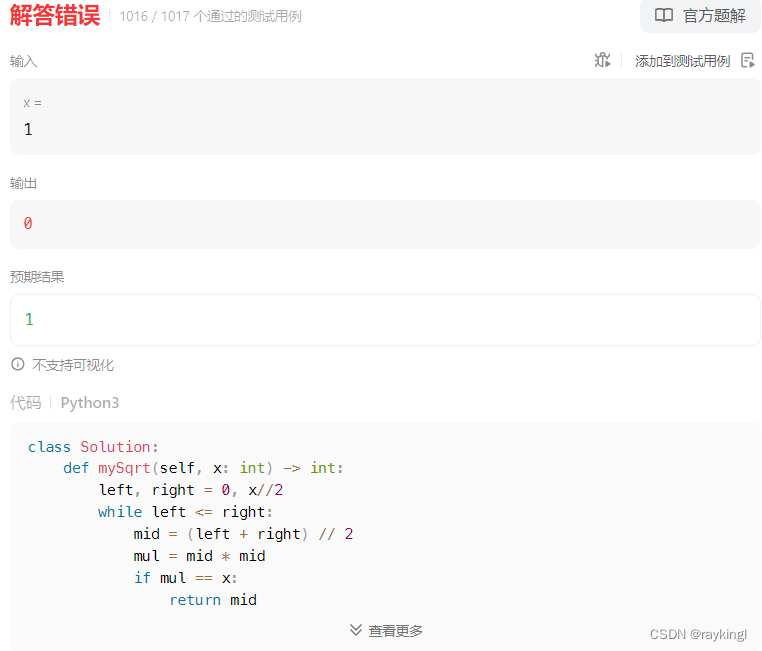
??此時未通過x=1的測試用例，此時預期結果為1但返回0，仔細觀察代碼，right初始值為2整數x，對于1，結果為0，因此初始化出現了問題，優化如下：

class Solution:def mySqrt(self, x: int) -> int:left, right = 0, x//2+1while left <= right:mid = (left + right) // 2mul = mid * midif mul == x:return midelif mul < x:left = mid + 1else:right = mid - 1return right

3.2 Java

class Solution {public int mySqrt(int x) {int left = 0, right = x / 2 + 1;while (left <= right){int mid = (left + right) / 2;int mul = mid * mid;if (mul == x){return mid;}else if (mul < x){left = mid +1;}else{right = mid - 1;}}return right;}
}

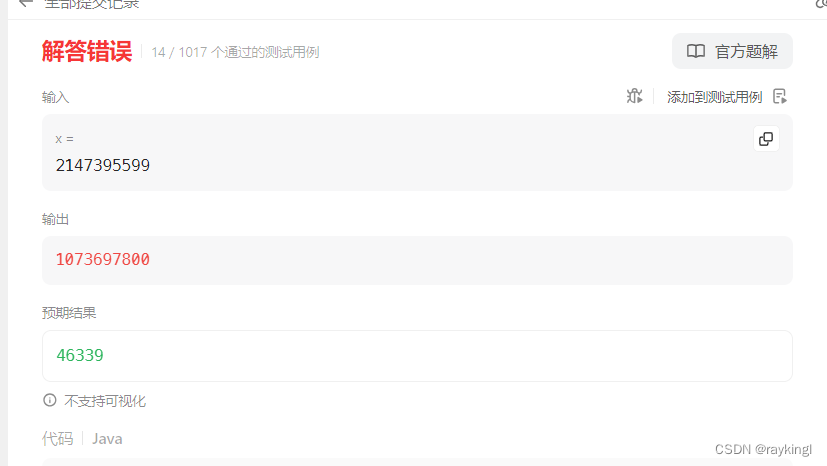
??對于測試案例x=2147395599運行錯誤，直接返回了right初始值的結果，說明一直觸發的是中間值平方小于x，這明顯是錯誤的，考慮到Java是嚴格聲明和定義數據類型的，因此錯誤在于內存溢出，超出Java的int類型的取值范圍，故中間值使用long整型，優化如下：

class Solution {public int mySqrt(int x) {int left = 0, right = (int)(x / 2 + 1);while (left <= right){int mid = (int) (left + right) / 2;long mul = (long)mid * mid;if (mul == x){return mid;}else if (mul < x){left = mid + 1;}else{right = mid - 1;}}return right;}
}

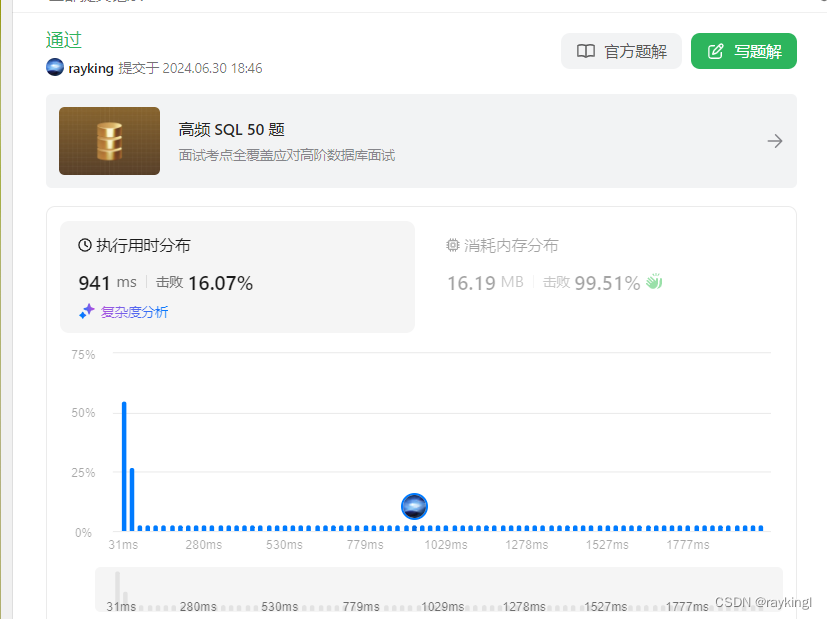
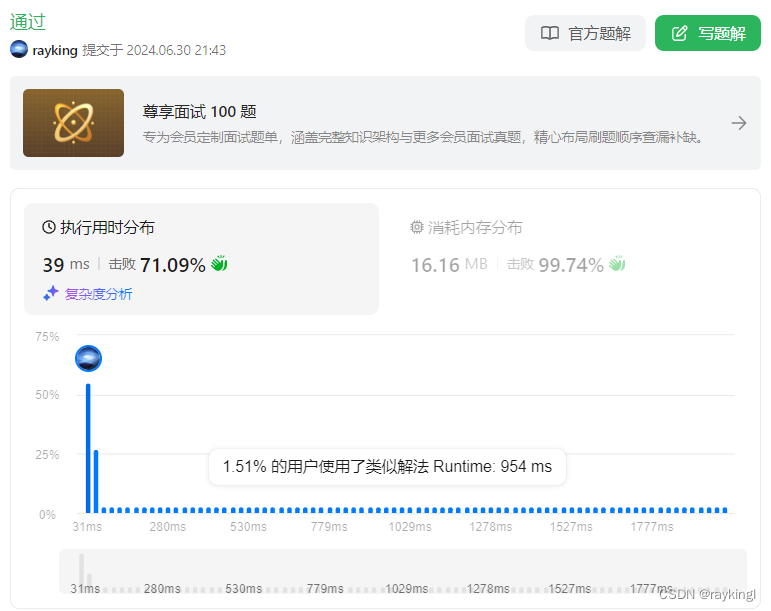
??執行用時不必過于糾結，對比可以發現，對于python和java完全相同的編寫，java的時間一般是優于python的；至于編寫的代碼的執行用時擊敗多少對手，執行用時和網絡環境、當前提交代碼人數等均有關系，可以嘗試完全相同的代碼多次執行用時也不是完全相同，只要確保自己代碼的算法時間復雜度滿足相應要求即可，也可以通過點擊分布圖查看其它coder的code。