目錄
- 一、基礎知識
- 1.1 顯著性檢驗
- 1.2 等方差T檢驗、異方差T檢驗
- 1.3 單尾p、雙尾p
- 1.3.1 檢驗目的不同
- 1.3.2 用法不同
- 1.3.3 如何選擇
- 二、Excel
- 2.1 統計分析工具
- 2.1.1 添加統計分析工具
- 2.1.2 數據分析
- 2.2 公式 -> 插入函數 -> T.TEST
- 三、RStudio
一、基礎知識
參考:
- 1.什么是顯著性檢驗? 2.為什么要做顯著性檢驗? 3.怎么做顯著性檢驗?
- excel----檢驗
- 如何用python來做假設檢驗
- 【統計科普】五分鐘輕松掌握三大 t 檢驗 - 獨立樣本t檢驗、配對樣本t檢驗與單樣本t檢驗
1.1 顯著性檢驗
- 什么是顯著性檢驗?
- 在統計學中,顯著性檢驗是“統計假設檢驗”(Statistical hypothesis testing)的一種,顯著性檢驗是用于檢測科學實驗中實驗組與對照組之間是否有差異以及差異是否顯著的辦法。
- 若原假設為真,而檢驗的結論卻勸你放棄原假設。此時,我們把這種錯誤稱之為第一類錯誤。通常把第一類錯誤出現的概率記為α
- 若原假設不真,而檢驗的結論卻勸你采納原假設。此時,我們把這種錯誤稱之為第二類錯誤。通常把第二類錯誤出現的概率記為β
- 通常只限定犯第一類錯誤的最大概率α, 不考慮犯第二類錯誤的概率β。我們把這樣的假設檢驗稱為顯著性檢驗,概率α稱為顯著性水平。顯著性水平是數學界約定俗成的,一般有α =0.05,0.01的情況。代表著顯著性檢驗的結論錯誤率必須低于5%或1%
- 為什么要做顯著性檢驗?
- 怎么做顯著性檢驗?
- 在這個問題下可以根據顯著性水平α和0.05的關系由法則"大同小異"得出是否存在顯著差異。
- “大同”:顯著性水平α>0.05,王先森的兩家分公司銷售額大致相同,不存在顯著性差異。
- “小異”:顯著性水平α<0.05,王先森的兩家分公司銷售額不相同,存在顯著性差異。
1.2 等方差T檢驗、異方差T檢驗
- 等方差T檢驗(Equal variance T-test):這種T檢驗假設兩個樣本的方差相等。當兩個樣本的方差相似時,可以使用等方差T檢驗。
- 異方差T檢驗(Unequal variance T-test):這種T檢驗假設兩個樣本的方差不相等。當兩個樣本的方差差異較大時,應該使用異方差T檢驗。
- 如果樣本的方差差異較小,可以選擇等方差T檢驗,否則選擇異方差T檢驗。
- 自由度=n-1
注:結果顯示
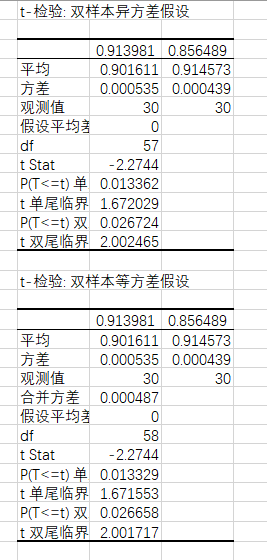
1.3 單尾p、雙尾p
- 雙尾T檢驗(Two-tailed T-test):這種T檢驗用于檢測兩個樣本之間的差異是否顯著。它能夠檢測到樣本均值在兩個方向上的差異,即是否存在統計學上顯著的差異。
- 單尾T檢驗(One-tailed T-test):這種T檢驗用于檢測兩個樣本之間的差異是否顯著,并且指定了一個方向。它只檢測樣本均值在指定方向上的差異,即是否存在統計學上顯著的正向或負向差異。
- 如果你對分割結果的差異沒有明確的方向性假設,可以選擇雙尾T檢驗。如果你有一個明確的方向性假設,可以選擇單尾T檢驗。
- 雙尾=單尾*2
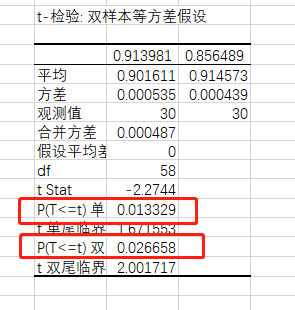
1.3.1 檢驗目的不同
- 雙尾檢驗(也就是雙側檢驗)是要檢驗樣本平均數和總體平均數,或樣本成數有沒有顯著差異。
- 單尾檢驗(也就是單側檢驗)目的是檢驗樣本所取自的總體參數值是否大于或小于某個特定值。
1.3.2 用法不同
- 研究目的是想判斷兩個數據的均值是否不同, 需要用雙尾檢驗。
- 研究目的是僅僅想知道一個數據的均值是不是高于(或低于)另一個數據, 則可以采用單尾檢驗。
1.3.3 如何選擇
- 如果假設中有一參數和另一參數方向性的比較,比如"大于"、“好于”、"差于"等,一般選擇單尾檢驗。
- 如果只是檢驗兩參數之間是否有差異,就選擇雙尾檢驗。
- 如果問題是:中學生中,男女生的身高是否存在性別差異, 因為實際的差異可能是男生平均身高比女生高,也可能是男生平均比女生矮。這兩種情況都屬于存在性別差異。需要用雙尾檢驗。
- 如果問題為:中學生中,男生的身高是否比女生高,這個時候需要采用單尾檢驗。
- 要比較的兩個樣本統計量的總體參數事先無法肯定哪個大或者哪個小時,就要用雙尾檢驗,所得到的檢驗結果取P雙尾值。否則就取P單尾值。單尾檢驗強調的是方向性。
二、Excel
注意: 有兩種方式,一種是統計分析工具,一種是公式。
2.1 統計分析工具
2.1.1 添加統計分析工具
文件 -> 選項 -> 加載項 -> 轉到 -> 選中”分析工具庫“和”分析工具庫-VBA“ -> 確定
2.1.2 數據分析
數據 -> 數據分析 -> t-檢驗:雙樣本等方差假設 -> 確定

- 依次選擇所要對比的兩列數據,然后回車。α(A)是顯著性水平,0.05代表95%的可信度。

- 輸出結果:
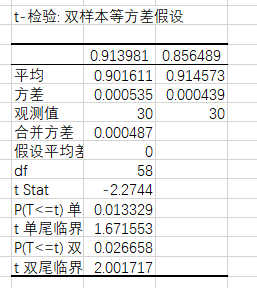
- df:自由度,用于其他統計量計算;
- P:顯著性水平,估計總體參數落在某一區間內,可能犯錯誤的概率;
- 查看差異顯著性(可信度):
- 差異顯著:0.01 < P value < 0.05
- 差異極顯著:P value < 0.01
2.2 公式 -> 插入函數 -> T.TEST




三、RStudio
"t.test()"函數:兩獨立樣本的T檢驗。
- 導入數據:
data<-read.csv("C:\\Users\\30330\\Desktop\\iou.csv", header = T)
- 數據分組:假設你的數據具有兩個組別,分別命名為"Ours"和"FCN"。
group1 <- data$Ours
group2 <- data$FCN
- 執行T檢驗:
result <- t.test(group1, group2)
- 打印T檢驗結果:
print(result)
- 結果顯示:













)



)


