一、MQ消息集成的定義
MQ消息集成是通過消息中間件(Message Queue)實現的一種數據集成方式。它通過將數據發送到中間件中,再從中間件中接收數據,實現不同系統之間的數據交換。在MQ消息集成中,發送者和接收者之間不需要直接建立連接,而是通過消息中間件來實現數據傳輸。
消息中間件是一種基于異步通信模式的中間件,它將數據存儲在隊列中,并在接收者準備好之后將數據傳輸給接收者。這種方式可以避免因為接收者忙碌或故障而導致數據傳輸失敗的情況。
二、MQ消息集成的主要特點和功能
- 異步通信:發送者將消息放入消息隊列后即可返回,不需要等待接收者的響應。這種異步方式可以提升系統的響應速度和吞吐量。
- 解耦和靈活性:消息隊列將消息發送者和接收者解耦,使它們可以獨立地進行開發、部署和擴展。發送者和接收者之間只需了解消息的格式和協議,而不需要了解對方的具體實現。
- 可靠性和消息傳遞保證:消息隊列通常提供了消息持久化、消息傳遞的可靠性保證,確保即使在發送者或接收者宕機或網絡故障的情況下,消息也能夠安全地傳遞。
- 負載均衡:通過消息隊列可以實現多個消費者并發處理消息,從而實現負載均衡和系統的高可用性。
- 消息順序保證:某些消息隊列可以確保消息按照發送的順序被接收和處理,保證消息的順序性。
三、MQ消息集成的應用場景
- 微服務架構:不同微服務之間通過消息隊列進行解耦,實現異步通信,提升系統的靈活性和可擴展性。
- 任務隊列和工作流:用于管理和調度異步任務和工作流程,例如批量處理、定時任務等。
- 事件驅動架構:通過發布/訂閱模式實現事件的傳遞和處理,用于實現系統內部事件驅動的應用程序。
- 日志處理:將系統日志通過消息隊列發送到日志分析系統或存儲系統,實現異步日志處理和分析。
- 實時數據處理:在大數據和實時計算場景下,通過消息隊列傳遞實時生成的數據,支持數據流處理和分析。
總之,MQ消息集成通過消息隊列實現了不同組件之間的松耦合、異步通信,提升了系統的可靠性、靈活性和性能,是現代分布式系統中重要的基礎設施之一。
四、MQ消息集成常見的模式
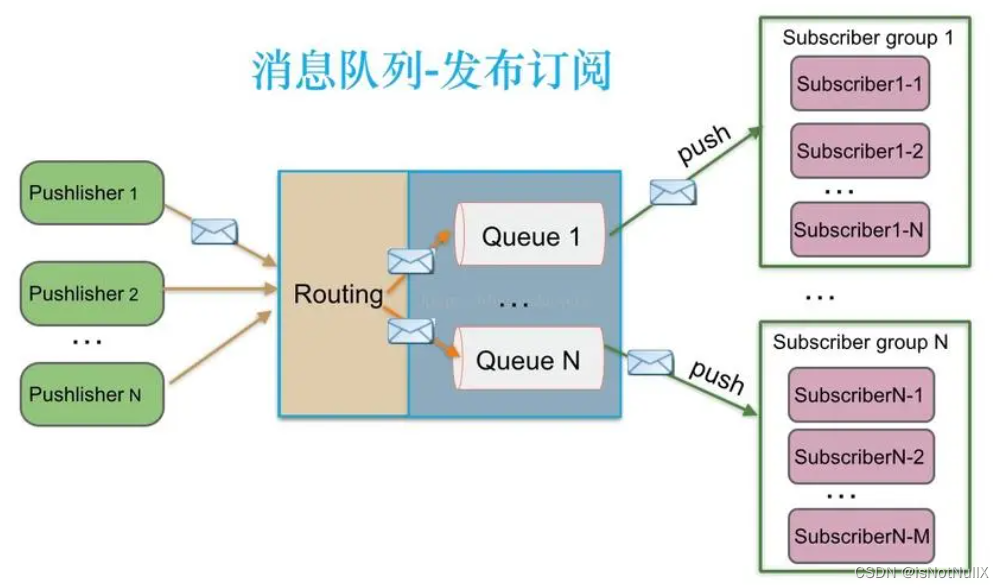
1.發布-訂閱模式(Publish-Subscribe):
發布-訂閱模式是MQ消息集成中最常見的模式之一。在這種模式下,消息發布者(Publisher)將消息發布到一個或多個主題(Topic),而訂閱者(Subscriber)可以訂閱感興趣的主題并接收相應的消息。消息被廣播給所有訂閱了該主題的訂閱者,實現了一對多的消息傳遞。
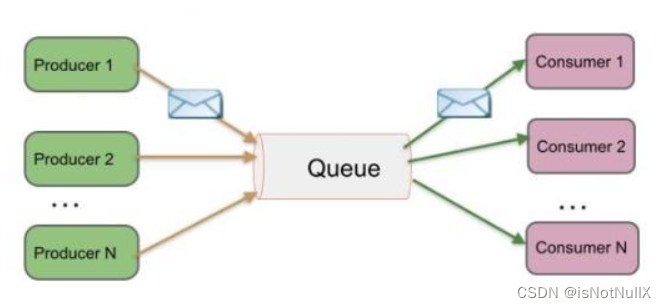
2.點對點模式(Point-to-Point):
點對點模式也稱為隊列模式。在這種模式下,消息發送者(Producer)將消息發送到特定的隊列(Queue),而消息接收者(Consumer)從隊列中獲取消息進行處理。每個消息只會被一個消息接收者消費,實現了一對一的消息傳遞。
3.請求-應答模式(Request-Reply):
請求-應答模式是一種同步的消息模式,用于交互式的請求和響應。發送方發送一個請求消息,接收方接收并處理請求后,發送一個響應消息給發送方。這種模式常用于需要立即響應的情況,如RPC(遠程過程調用)。
4.點對多模式(Point-to-Multipoint):
點對多模式是一種介于發布-訂閱模式和點對點模式之間的模式。在這種模式下,消息發送者將消息發送到特定的隊列,但可以有多個消息接收者從該隊列中獲取消息進行處理。每條消息只會被一個消息接收者消費,但可以有多個接收者并行處理來提高處理能力。
五、MQ消息集成的實現方式
MQ消息集成可以通過多種消息中間件實現,例如ActiveMQ、RabbitMQ、Kafka等。這些消息中間件都提供了豐富的API和配置選項,可以根據實際需求進行配置和使用。
在使用MQ消息集成時,需要注意以下幾點:
●消息中間件的選取:根據實際需求選擇合適的消息中間件。
●消息格式的定義:定義消息的格式和內容,以便發送方和接收方能夠正確地解析和使用消息。
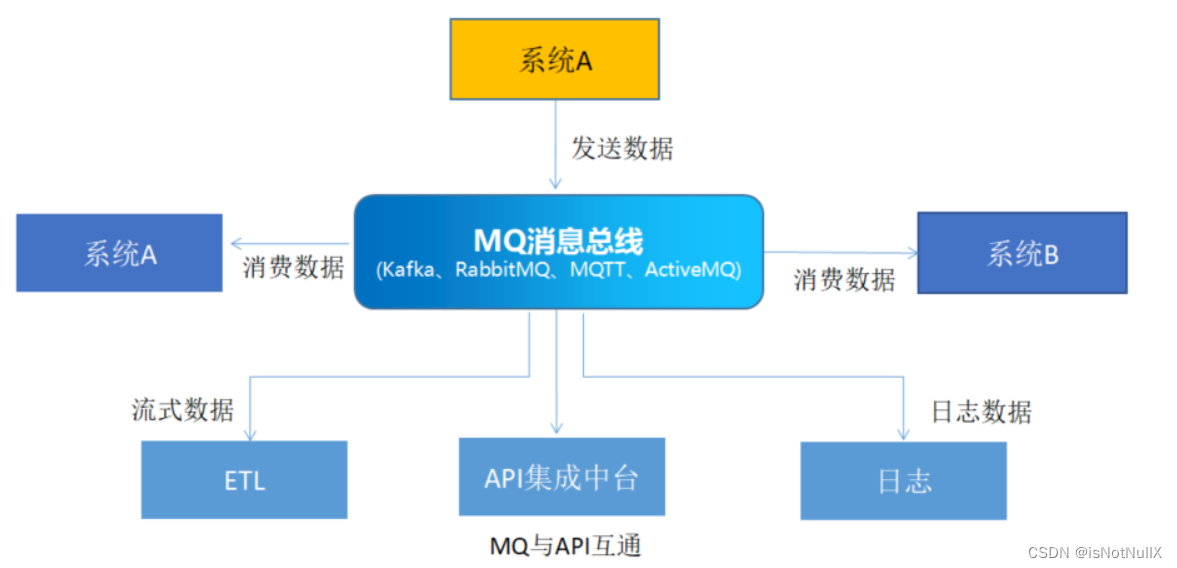
●異常處理和重試機制:在消息傳輸過程中,可能會發生異常或消息丟失的情況,需要有相應的異常處理和重試機制。當需要將實時產生的數據流整合到ETL流程中時,則需要ETL工具的加入:
一些MQ消息集成工具具有高吞吐量和低延遲的特點,能夠處理大量的消息并保證數據傳輸的可靠性。對于需要處理大規模數據的ETL流程尤為重要。除了MQ消息集成,還有Kafka等消息隊列,企業可以選擇合適的中間件進行使用。FineDataLink是一款數據集成工具,其中包含ETL功能支持使用 Kafka 作為數據同步的中間件,實現高效的數據傳輸和處理,提高整體性能和效率。
FineDataLink是一款低代碼/高時效數據集成工具,提供了強大的ETL功能和多種技術架構支持,根據實際需求,企業可以使用合適的消息集成工具和ETL工具進行集成,構建靈活高效的數據集成和處理流程。
了解更多請點擊:FineDataLink功能體驗
往期內容推薦:
6種ETL計算引擎介紹-CSDN博客
「ETL趨勢」FDL數據開發支持版本管理、實時管道支持多對一、數據源新增支持神通-CSDN博客
什么是API?如何進行API對接?_api對接是對接到服務器的嗎-CSDN博客



















