參考

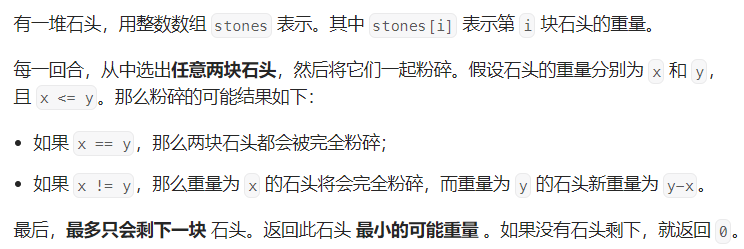
備注: 當物體容量也等同于價值時, 01背包問題的含義則是利用好最大的背包容量sum/2, 使得結果盡可能的接近或者小于 sum/2
等價: 盡可能的平分成相同的兩堆, 其差則為結果, 比如 (a+b+c)-d, (a+c)-(b+d) , 最終的結果是一堆減去另外一堆的和, 問題則轉換成01背包

class Solution {
public:int lastStoneWeightII(vector<int>& stones) {int sum = 0;for (int i = 0; i < stones.size(); i++) {sum += stones[i];}vector<int> dp(sum / 2 + 1, 0);for (int i = 0; i < stones.size(); i++) {for (int j = sum / 2; j >= 0; j--) {if (j - stones[i] >= 0) {dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);}}}return (sum - dp[sum / 2]) - dp[sum / 2];}
};

回溯法會超時

轉換成01背包問題:

• A + B = sum
• A - B = target
• A = (target + sum) / 2
• B = (sum - target) / 2
  其中A相當于weigh, nums[i]相當于價值
  當 A = (target + sum) / 2 向下取整時, 說明不存在結果
  當 abs(target) > sum 時不存在

五部曲:

1. dp[j]: 填滿j（包括j）這么大容積的包，有dp[j]種方法 (假設A為容量)
2. 
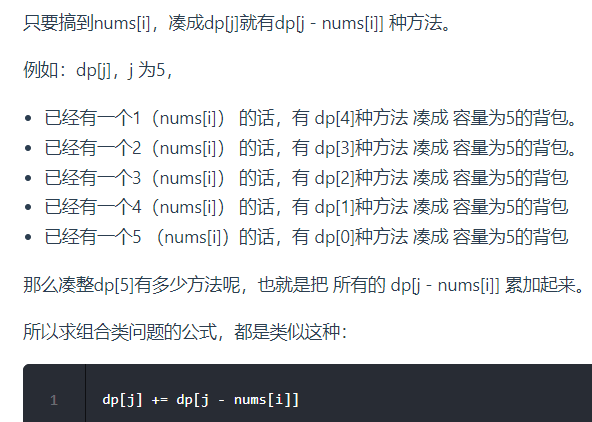
3. 初始化: dp[0] = 1

class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {int sum = 0;for (int i = 0; i < nums.size(); i++) {sum += nums[i];}int A = (target + sum) / 2;if ((target + sum) % 2) return 0;if (abs(target) > sum) return 0;vector<int>dp(A + 1, 0);dp[0] = 1;for (int i = 0; i < nums.size(); i++) {for (int j = A; j >= nums[i]; j--) {dp[j] += dp[j - nums[i]];}}return dp[A];}
};