完全背包
完全背包物品可以無限使用
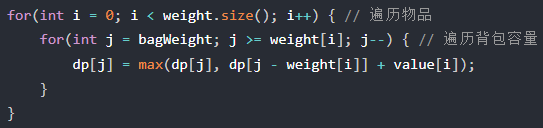
01背包核心代碼
- 01背包中的二維dp數組的兩個for遍歷可顛倒, 而一維dp數組的一定先遍歷物品再遍歷背包容量
- 狀態轉移方程(背包容量一定為遞減)
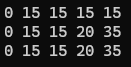
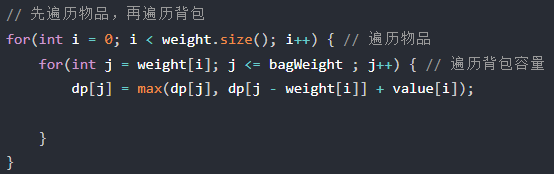
完全背包核心代碼 (只在完全背包中一維dp數組嵌套順序可顛倒, 實際題目需要確定遍歷順序)
-
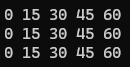
狀態轉移方程(先物品, 再背包, 并且為遞增, 橫向更新數值)
-
由于都是由前一個狀態推導, 所以只在純完全背包問題中可以顛倒, 區別是行更新或者列更新

-
狀態轉移方程(先背包, 再物品, 遞增順序, 且為縱向更新)

518. 零錢兌換 II


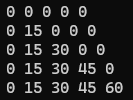
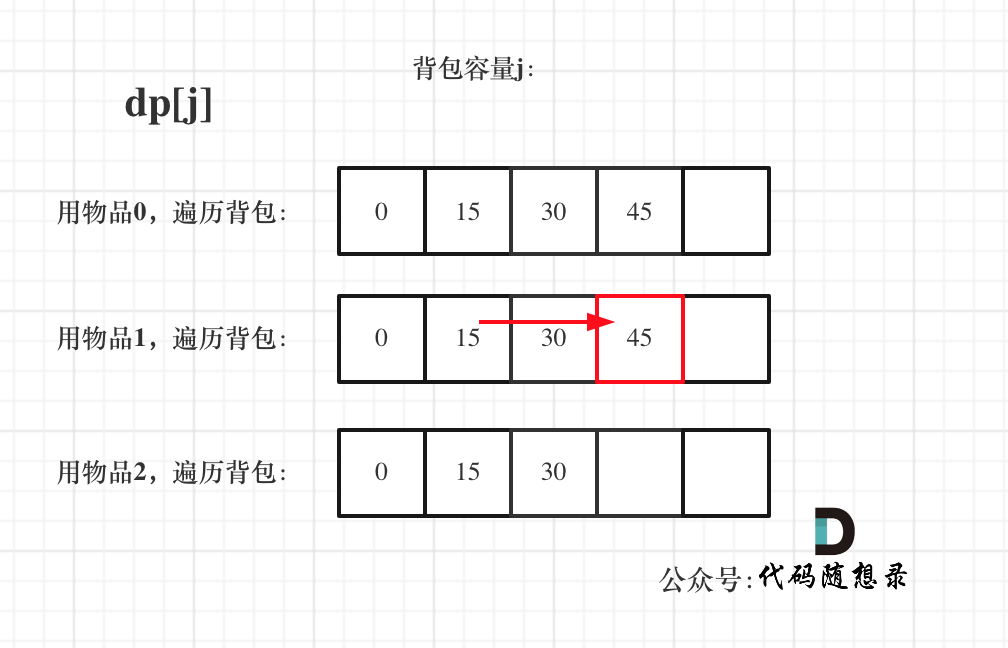
遞推公式: dp[j] += dp[j - coins[i]]
概括物體和背包的遍歷情況
- 先遍歷物品(coins)后遍歷背包(amount), 物品 coins[i] 只能在本次循環中添加, 下一次循環才添加coins[i+1], 只有一種: coins[i] coins[i + 1]
- 先遍歷背包后遍歷物品時, coins[i] coins[i + 1] 與 coins[i + 1] coins[i] 會當成不同的情況處理
先物品后背包(僅僅只是組合問題, 不存在排列)

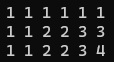
先背包后物品(存在排列問題)


class Solution {
public:int change(int amount, vector<int>& coins) {vector<int> dp(amount + 1, 0);dp[0] = 1;for (int i = 0; i < coins.size(); i++) {//遍歷物品for (int j = 0; j <= amount; j++) {//遍歷背包if (j - coins[i] >= 0)dp[j] += dp[j - coins[i]];}}return dp[amount];}
};
377. 組合總和 Ⅳ


class Solution {
public:int combinationSum4(vector<int>& nums, int target) {vector<int> dp(target + 1, 0);dp[0] = 1;for (int j = 0; j <= target; j++) {for (int i = 0; i < nums.size(); i++) {if (j - nums[i] >= 0 && dp[i] < INT_MAX - dp[i - nums[j]]) //防兩個int相加會溢出dp[j] += dp[j - nums[i]];}}return dp[target];}
};
70.爬樓梯(進階版)


)



)












)