本文簡要闡述STK中光照計算的模型。

在航天任務中，通常需要分析地面站、飛行器在一定時間內的光照情況，具體包括：

1. 地面站處在光照區和陰影區的具體時間范圍；
2. 考慮地形遮擋后，地面站的光照區和陰影區的變化情況；
3. 飛行器繞地飛行過程中，處于光照區和陰影區的具體時間范圍；
4. 地面站當地水平系下，太陽方位角、高度角的變化；
5. 飛行器軌道器或本體系下，太陽方位角、高度角的變化。

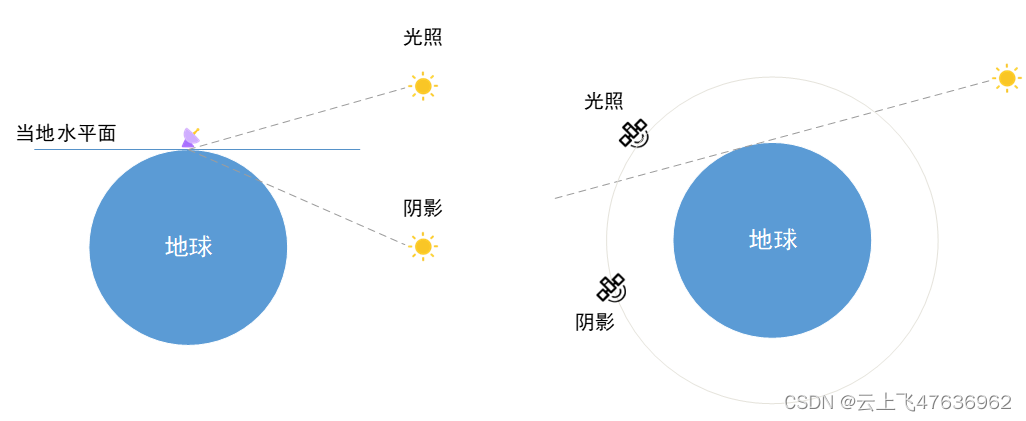
光照計算時，主要考慮的是地球對太陽的遮擋（其它天體也是類似的），見下圖所示地面站和飛行器的光照示意圖。

對于地面站（左圖），考慮地球遮擋，當太陽在當地水平面之上時（對應的太陽的高度角大于0），即地面站為光照狀態；反之則為陰影狀態。

對于空間飛行器（上面右圖），如衛星，當飛行器與太陽連線不被地球遮擋時，則飛行器為光照狀態；反之則為陰影狀態。

實際計算時，地球形狀考慮為橢球體。

下面根據以上所涉及到的光照場景，詳細討論。

坐標系及太陽方位角、高度角

涉及到太陽位置計算時，通常涉及到太陽的方位角和高度角概念，因此首先確定好常用的坐標系和太陽方位角和高度角的定義。

地面站地平坐標系

地面站觀測太陽時，采用當地水平坐標系（也稱北東地坐標系），簡稱LH坐標系（Local Horizontal），其定義如下：

1. X軸指向當地北方向；
2. Y軸指向當地東方向；
3. Z軸指向當地天底方向。

XY平面為當地水平面，垂直于地球橢球體法線，見下圖。

下圖給出了地面站LH系下的太陽方位角和高度角。

飛行器VVLH系

飛行器觀測太陽時，通常采用軌道坐標系，簡稱VVLH坐標系（Vehicle Velocity, Local Horizontal），其定義如下：

1. X軸約束在慣性系速度方向（由Y叉乘Z得到）；
2. Y軸指向軌道面負法向；
3. Z軸指向地心方向。

下圖為飛行器的VVLH坐標系以及太陽方向矢量的高度角和方位角示意圖。

太陽方位角和高度角

在地面站地平坐標系或者飛行器VVLH坐標系中，太陽方位角（Azimuth，簡稱Az）和高度角（Elevation，簡稱El）的定義如下圖。

1. 方位角定義為：X軸與太陽方向矢量在XY平面內的投影矢量的夾角，+X軸為零點，向+Y軸方向為正；
2. 高度角定義為：太陽方向矢量與XY平面的夾角，-Z軸方向為正。

注意，對于飛行器本體坐標系（Body），則高度角以+Z軸方向為正。

根據以上定義，實際計算時，首先求得某時刻太陽（通常為視太陽）在地面站LH系或飛行器VVLH系的位置，設為${\text{R}}_s$：
$${\text{R}}_s={\left[X_s,Y_s,Z_s\right]}^T$$

則太陽方位角Az和高度角El計算如下：
$$\{\begin{array}{r}Az=tan{2}^{?1}(Y_s,X_s)\\ El=si{n}^{?1}(?Z_s/R_s)\end{array}$$

光照計算模型

無論是地面站還是飛行器，在精確計算光照和陰影的時間時，必須考慮到以下因素：

1. 太陽圓盤的大小，以及被遮擋的部分大小；
2. 對于地面站，當地水平面附近地形遮擋的影響；
3. 對于空間飛行器，考慮地球的遮擋。

同時，太陽的光照狀態分為以下三種情形：

1. 光照：太陽圓盤完全不被遮擋，地面站或飛行器處于完全光照狀態，太陽光照強度因子為1；
2. 半影：太陽圓盤部分被遮擋，地面站或飛行器處于半影狀態，太陽光照強度因為0-1之間的小數；
3. 全影：太陽圓盤完全被遮擋，地面站或飛行器處于完全陰影狀態，太陽光照強度因子為0。

首先給出地面站的光照計算模型，見下圖。

某時刻，以觀測點為中心，視太陽方向的地形最大仰角為${\alpha }_t$，視太陽中心（即太陽位置）方向與地形最大仰角方向的夾角為${\alpha }_g$，太陽圓盤視半徑為${\alpha }_s$。

不考慮地形時(${\alpha }_t=0$)，${\alpha }_g$即為視太陽方向與當地水平面的夾角，即太陽仰角El。

太陽圓盤視半徑${\alpha }_s$由下式給出：
$${\alpha }_s=si{n}^{?1}\frac{R_o}{R_s}$$
上式中，$R_o$為太陽圓盤半徑，取值為695700km，對應的視半徑約為0.27°，具體數值與太陽的距離變化而稍有不同。

下圖為飛行器的光照計算模型示意圖。與地面站不同的是，不需要考慮地形的遮擋，轉而考慮地球的遮擋。

某時刻，以觀測點為中心，地心方向與地球邊緣方向的夾角（稱為地球視半徑）為${\alpha }_t$，視太陽中心（即太陽位置）方向與地球邊緣方向的夾角為${\alpha }_g$，太陽圓盤視半徑為${\alpha }_s$。觀測點到地球的距離向量為${\text{R}}_E$。

地球視半徑${\alpha }_t$可由下式給出:
$${\alpha }_t=si{n}^{?1}\frac{R_e}{R_E}$$
上式中，$R_e$為地球赤道半徑，常取6378.14km。

根據上述兩種光照模型，太陽光照狀態的判別依據如下：
$$?\begin{array}{rl}光照:& {\alpha }_g>{\alpha }_s\\ 陰影:& {\alpha }_g<?{\alpha }_s\\ 半影:& ?{\alpha }_s\le {\alpha }_g\le {\alpha }_s\end{array}$$