題目鏈接
最大子序列的分數
題目描述
注意點
- n == nums1.length == nums2.length
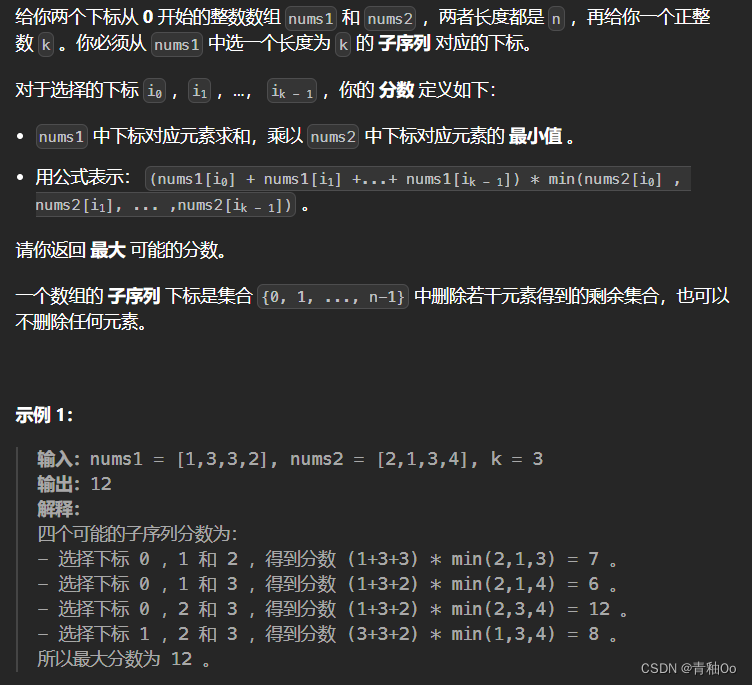
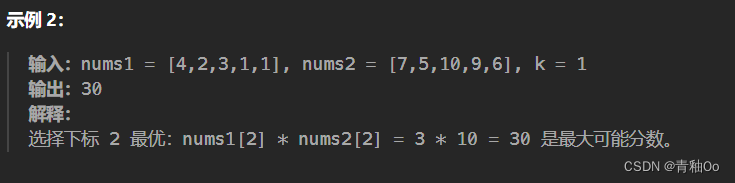
- 從nums1和nums2中選一個長度為k的子序列對應的下標
- 對nums1中下標對應元素求和,乘以nums2中下標對應元素的最小值得到子序列的分數
- 0 <= nums1[i], nums2[j] <= 100000
- 1 <= k <= n
解答思路
- 初始想到的是深度優先遍歷,傳遞nums1子序列的和以及nums2中值最小的元素,當選擇了k個元素時,計算分數,統計分數的最大值,但是超時
- 參照題解,可以先將nums2從大到小進行排序,因為子序列中nums1和nums2的下標都是相同的,所以需要記錄對nums2中的值進行排序后記錄的是新下標newIdx
- 使用PriorityQueue存儲子序列中nums1的元素,堆頂對應的是元素的最小值。在更換子序列的元素時,按照排好序的nums2將后續的元素newIdx加入進來,同時將之前子序列中某個元素彈出(不論彈出哪個元素nums2的最小值都是nums2[newIdx]),彈出的元素應該是子序列中nums1的最小值,也就是PriorityQueue的堆頂
代碼
class Solution {public long maxScore(int[] nums1, int[] nums2, int k) {int n = nums1.length;Integer[] idxArr = new Integer[n];for (int i = 0; i < n; i++) {idxArr[i] = i;}// nums2從大到小進行排序,僅記錄下標位置Arrays.sort(idxArr, (x, y) -> (nums2[y] - nums2[x]));// 堆頂為最小值PriorityQueue<Integer> queue = new PriorityQueue<>((x, y) -> (x - y));long sum1 = 0;for (int i = 0; i < k; i++) {int idx = idxArr[i];sum1 += nums1[idx];queue.offer(nums1[idx]);}long res = sum1 * nums2[idxArr[k - 1]];for (int i = k; i < n; i++) {// 此時nums2[idx]是nums2中子序列的最小值// 滿足上述條件且nums1中相應子序列和最大:加上idx處的元素值,減去前面子序列中的最小元素int idx = idxArr[i];// nums2[idx]也比之前的子序列小,sum1也比之前的子序列小,分數一定更小,不考慮if (nums1[idx] < queue.peek()) {continue;}sum1 -= queue.poll();sum1 += nums1[idx];queue.offer(nums1[idx]);res = Math.max(res, sum1 * nums2[idx]);}return res;}
}
關鍵點
- 將nums2中的元素從大到小進行排序,初始選擇k個元素,對應nums2最小值就是nums2[k - 1],按順序加入元素,彈出之前某個元素,保證快速找到子序列中nums2的最小值
- 根據nums2選擇好子序列后,根據其下標將nums1中對應元素添加到PriorityQueue中(堆頂為最小值),保證快速找到nums2[newIdx]是最小值時nums1的元素和最大的子序列
- 如果加入新的元素下標對應在nums1中的元素值比PriorityQueue堆頂元素更小,說明此時分數一定比上一個子序列分數更低(nums1子序列之和更小,nums2子序列中的最小值也更小),不考慮










)







:靜態、友元和內部類)
