——貪心算法—

1?檸檬水找零

2?將數組和減半的最少操作次數

3??最大數

4?擺動序列

5?最長遞增子序列

6?遞增的三元子序列

7?最長連續遞增序列

8?買賣股票的最佳時機

9?買賣股票的最佳時機 II

10?K 次取反后最大化的數組和

11?按身高排序

12?優勢洗牌

13?最長回文串

14?增減字符串匹配

15?分發餅干

16?最優除法

17?跳躍游戲 II

18?跳躍游戲

19?加油站

20?單調遞增的數字

21?壞了的計算器

22?合并區間

23?無重疊區間

24?用最少數量的箭引爆氣球

25?整數替換

26?俄羅斯套娃信封問題

27?可被三整除的最大和

28?距離相等的條形碼

29?重構字符串

貪心入門概念：

貪心算法的原理其實概念很簡單，就是一個解決問題的策略，從局部的最優解推導出全局的最優解，就是貪心的思路。

貪心的步驟一般如下：

1 將解決問題的過程分為若干步；

2 解決每一步的時候都選擇在當前看起來“最優”的解法；

3 “希望”能夠依此得到全局最優解。

為什么說是“希望”得到全局最優解呢？因為我們從局部最優解推導過來的全局解并不一定是全局的最優解。

為了快速入門貪心，我們可以用以下幾個示例來學習貪心的策略：

1 找零問題：給定紙幣的種類，要求用最少數量的紙幣張數找零出指定金額。

比如我們給定[20,10,5,1]四類紙幣面額，要求我們湊出28元，那么我們如何思考最優解呢？我們先將問題拆分成多個步驟，其實每一個步驟都需要選擇一張紙幣，那么我們要最終的紙幣張數最少，我們就需要一張紙幣起到的作用最大，那么我們每一次選擇紙幣面額都去選擇最大的面額，比如第一次選擇，需要湊出28元，我們選擇20元的面額一張，此時還剩下8元需要找零，第二次選擇一張5元的紙幣，以此類推，最終選擇了1張20元，1張5元和3張1元。這種場景下，我們從局部推導出來的解就是一個全局的最優解。

但是假如我們給定[10,6,5,1]這四種面額，去湊齊18元找零，如果還是按照上面的貪心策略來做，就會得到：1張10元，1張5元和3張1元，一共5張紙幣，但是其實本題的最優解是使用3張6元面額的紙幣就夠了。? 所以我們使用局部最優策略得到的解并不一定是全局最優的。

2 最小路徑和：給定一個二位網格圖，每一步只能向右或向下，找出從左上角走到右下角的最小的路徑和。

我們將問題劃分為多個步驟的話，那么其實每一步就是選擇向下走還是向右走，那么每一步都貪心來思考，我們其實在(x,y)位置的時候，會選擇board[x+1][y] , board[x][y+1] 這兩個中較小的位置來作為下一步，這就是一種局部貪心的策略，但是這樣推導出來的解并不一定是全局的最優解，比如在這樣的而一個二維網格圖中：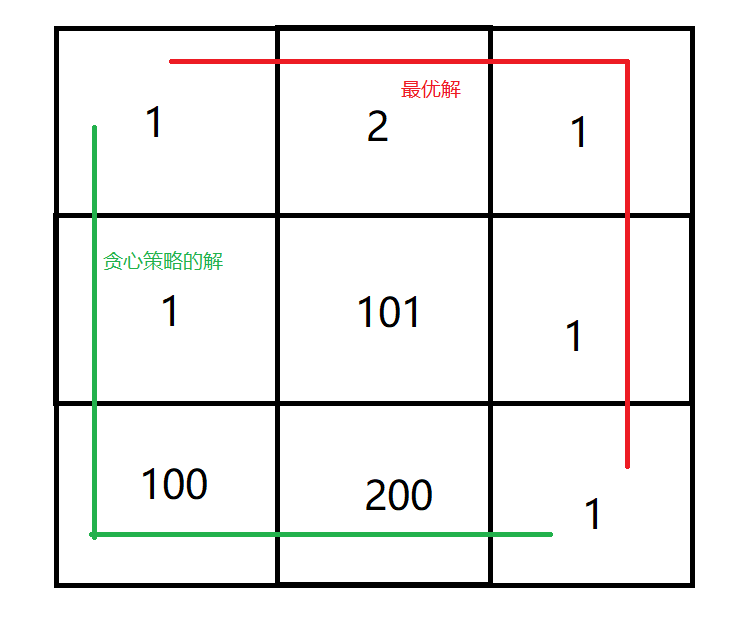

3 背包問題：給定一個背包容積為V，給定一系列物品的體積vi和價值wi，求出背包能裝的最大的價值

如果使用貪心策略來做的話，我們要使得固定體積內得價值最大，那么就要使得單位體積內的價值最大，因此我們需要預處理出每個物品的單位體積的價值，每次選擇單位體積價值最大的物品放進去(如果體積足夠的話)。

當然這種貪心策略也不一定能夠得到全局的最優解。

貪心的特點

從上面的幾個例題我們也能知道，貪心策略是作用在局部的，也就是每一個步驟來進行貪心選擇最優解，他并沒有全局的眼光，所以每一個步驟的最優解并不一定能得到全局的最優解。?

同時在每一步選擇最優解的時候，我們稱之為貪心策略，貪心策略是沒有模板的，我們需要根據每一個問題的場景來提出對應的貪心策略。

同時我們提出的貪心策略可能是“錯誤”的，這也就意味著貪心策略的正確性是需要證明的，而貪心策略的正確證明其實才是整個貪心算法的最重要的一點。因為貪心策略其實我們可以根據經驗提出很多，同時證明一個貪心策略是錯誤的我們只需要使用一個反例就行了，但是要證明貪心策略的正確性，是很復雜的，常見的證明方法有：

1 數學證明法

使用數學方法來證明，比如利用各種不等式，微分，積分等知識來證明貪心解就是最優解。

2 等效法

我們通過證明貪心解和最優解完全等效，就能夠證明貪心策略的正確性。

比如上面的找零問題，面額有[20,10,5,1]。

假設我們貪心求出的解，有A張20，B張10,C張5,D張1，而最優解有a張20，b張10，c張5，d張1。

在證明正確性之前，我們能夠證明 : B < 2 ，因為如果B大于2，那么我們其實會選擇一張20的而不是兩張10的； C < 2 , 因為如果C>2，每2張5元的我們會選擇用10元的而不是兩種5元；D < 5 同理。

我們只需要證明 a == A && B == b && C == c && D == d就能證明我們的貪心解和最優解是一樣的。

首先對于 A == a ，如果A?> a，那么證明最優解中，這些貪心解中多出的20元就需要用其他紙幣去湊，但是根據我們前面的到的BCD的關系，他們也適用于bcd，也就是說10元，5元和1元的紙幣我們最多只能夠湊出19元，根本湊不出20元，那么就能夠證明 A !> a 。

同理a !> A，這是從我們的貪心策略能夠推導出來的，因為貪心策略中是能選20就選20 ，那么A>=a。

根據 A>=a&&A!>a我們就能得出A==a。

同理我們也能推導出 B==b ,C==c,D==d。這樣我們就能用數學方法證明貪心策略的正確性。

3 交換論證法

比如我們的得到的貪心解是 : abcde。

而最優解是 bcdea。假設題目場景與返回的解的順序無關。

那么我們在一一對比貪心解和最優解是否一樣的時候，假設對比到第一個位置，我們發現a!=b，但是我們能夠直到在貪心解中一定會出現b，那么我們將貪心解的a和b交換位置。以此類推，能夠通過交換來達到貪心解和最優解的等效。

學習貪心的時候，其實對于我們來說，貪心策略和正確性的證明都是很困難的，不過我們不需要過分擔心，在初學貪心的時候，可能遇到的每一個題我們都想不出一種正確的貪心策略，這時候我們可以學習他人的貪心策略，如果有興趣也可以學習正確性的證明，我們需要在做題的過程中將他人的貪心策略吸收，后續遇到類似的題目就可以復用這些貪心策略。

當然如果我們想要更深入的學習貪心算法，那么貪心策略的正確性的證明還是邁不過去的坎。?

在本文中，我們注重于學習各種貪心策略，而不會著重講解正確性的證明。

1?檸檬水找零

860. 檸檬水找零 - 力扣（LeetCode）

題目解析：我們需要進行檸檬水的找零，每一杯檸檬水價格為5，顧客可能給我們5，10，和20三種面額的錢，我們需要對每一個顧客進行找零，如果能夠完成所有顧客而當找零，返回true，不能就返回false。

首先我們在想貪心策略的時候，要將整個問題拆解成多個相似的步驟，我們只需要在其中某一個步驟進行思考就行了。比如我們這里的每一步就是對每一個客人進行找零，在對第i個客人進行找零的時候，使用貪心的思想，在局部的貪心策略中不需要關注后續的客人能否找零。

由于顧客只會給我們三種面額，5不需要找零，10只能找零一張5元，而20需要找零15元，此時有兩種做法：1、找零3張5元；2、找零1張10元和1張5元。那么我們使用哪一種策略更優呢？

由于5元的面額我們既要在10元中用到，也要在20元用到，而10元面額只會在20的找零中用到，所以我們會盡可能的保留5元的紙幣，也就是說我們會優先考慮第2中策略來對20進行找零。

證明方法：交換論證法

由于對5元和對10元的找零策略沒有貪心的空間，所以我們只需要討論對20元找零的所有解就行了。

假設貪心解是:abcde,而最優解是:ebcda，此時貪心解和最優解的順序不同，可以通過交換順序等效。

也有可能: 貪心解abcdef，最優解是:abcdxy,比如對其中幾個20元的找零思路不同，那么說明不同的幾個20元找零時，貪心解用的是: 10+5 的組合，而最優解用的是: 5+5+5 的組合。此時雖然兩種找零策略不同，但是都能夠完成找零工作，由于貪心解用到了10元的紙幣，而此時最優解用的是5+5的紙幣，那么說明這兩種面額此時都是足夠的，那么我們完全也可以把貪心解的10元面額換成兩個5元面額，來使得貪心解和最優解等效。或者將最優解的兩張5元替換成一張10元可貪心解等效。

由于本題20元面額收完之后不會再用到，所以我們只需要存儲所擁有的5元和10元的數量就行了，代碼如下：

class Solution {
public:int cnt1 ,cnt2; //5元和10元的數量bool lemonadeChange(vector<int>& bills) {for(auto x : bills){if(x == 5) ++cnt1;else if(x == 10) --cnt1,++cnt2;else{if(cnt2 > 0) --cnt2,--cnt1;  //如果有10元就優先使用10元else cnt1 -= 3;//沒有10元就只能使用三張5元}// if(cnt1 < 0 || cnt2 < 0) return false;if(cnt1 < 0) return false; //由于我們只有在有10元的時候才會使用，而使用5元沒有判斷，只有5元的數量會花超}return true;}
};

2?將數組和減半的最少操作次數

https://leetcode.cn/problems/minimum-operations-to-halve-array-sum/

題目解析：給定一個數組nums，我們每一次可以選擇數組的一個數將其減半，可以對一個數多次操作。求出最少需要多少次減半操作才能使數組和減半。

每一次需要從nums中選出一個數進行減半操作，要使得操作的次數盡可能小，那么我們就需要讓每一次操作減去的數盡可能大，那么我們的貪心策略就是每一次操作選擇當前剩余元素中最大的數進行減半，直到減去的值大于等于原數組和的一半。

正確性：假設貪心解為：abcdef ，最優解為 abcdfe 或者 abcdeh

當貪心解和最優解只是順序不同時可以交換順序來達到等效，而如果最優解和貪心解在某些位置操作的元素不一樣，我們可以先對最優解進行降序排序，由于貪心解是按照從大到小的順序來操作元素的，那么如果最優解和貪心解的某一個元素不一樣，那么說明此時最優解選擇的元素一定是小于貪心解所選擇的元素的，而選擇較小的元素進行減半都能夠達到目標，那么自然在貪心解中選擇較大的元素也可以達到目的，或者說我們完全可以將最優解的該元素替換成貪心解中更大的元素，最優解的正確性依舊成立。

而我們每一次操作都需要選擇當前剩余的最大的元素進行減半，那么可以使用堆來維護所有的剩余元素。

代碼如下：

class Solution {
public:double EXP = 1e-10; //誤差int halveArray(vector<int>& nums) {priority_queue<double> pq;double sum = 0 , sub = 0;for(auto x : nums){sum += x;pq.push((double)x);}int res = 0;while(sub < sum && !abs(sub - sum) <= EXP){ //規定結果的誤差在10^-10內都算有效++res;double x = pq.top();pq.pop();sub += x;  //當我們操作的數的總和大于等于sum時，那么減掉的數自然就大于等于sum的一半了pq.push(x/2);}return res;}
};

3??最大數

https://leetcode.cn/problems/largest-number/

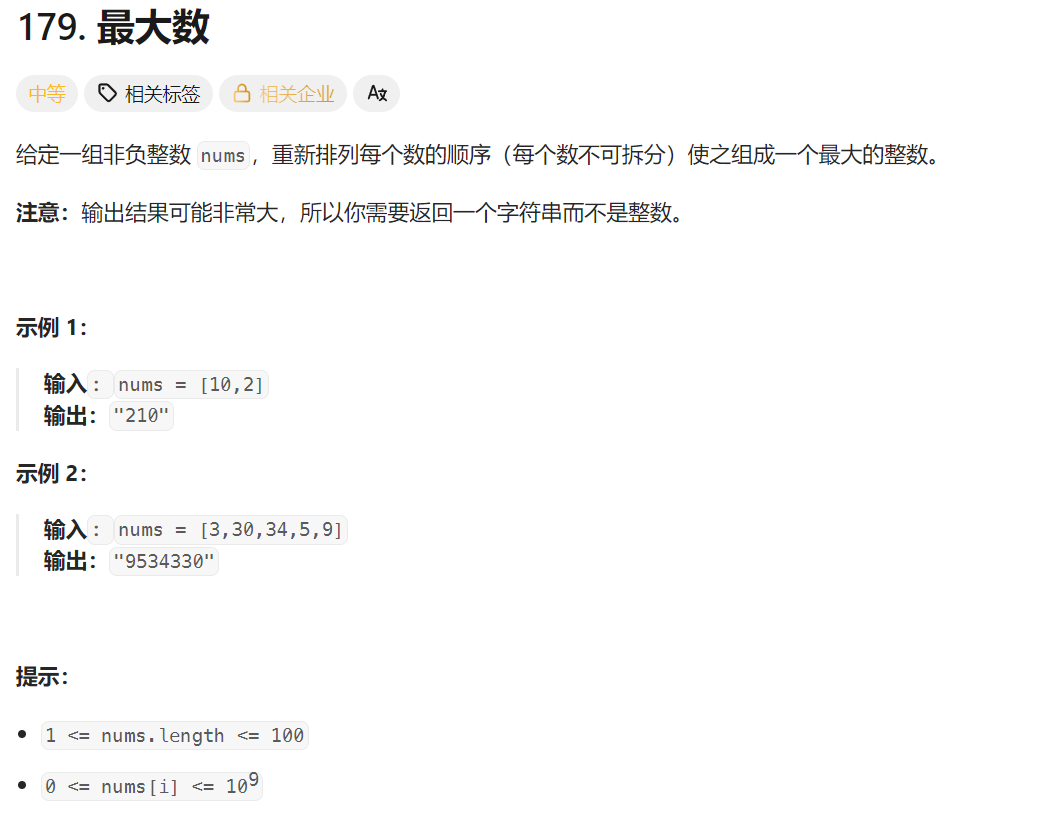
題目解析：給定一個非負整數數組，要求我們將數組中的數組合在一起，例如：1和2組合可以變成12和21。輸出能夠組合出來的最大的數。

如果nums中包括0，那么我們直到這些0一定不能作為前置0，作為前置0的時候一定會使得結果小于最優解。

在不包含前置0的情況下，我們按任意順序組成的數字的位數都是相同的，那么高位越大，結果就越大。

比如：3和12組成的數字，我們會選擇3作為高位，組成312 ，而不是123。

對于兩個數字，a和b，如果ab > ba ，那么我們就需要讓a排在b的前面。如果ab==ba，那么這兩個數字的順序無所謂，如果 ab < ba，那么需要讓b排在a的前面。那么這就是一種貪心的策略。

這種貪心策略如何實現呢？我們可以通過定義排序規則，通過排序來確定最終順序。

這個策略能夠作為排序規則需要三個性質：

1、完全性，兩個元素一定能夠確定大小關系，要么大于，要么等于，要么小于，而不會出現模糊的大小關系。

2、反對稱性：如果a>=b && b>=a ，那么 a==b；

3、傳遞性： a > b && b >?c ，那么需要能夠推導出 a >?c；

而為了方便比較，也就是將 a和b組成ab和ba的形式，我們可以將數字轉換成字符串來處理。

代碼如下：

class Solution {
public:string largestNumber(vector<int>& nums) {vector<string> str;for(int x : nums) str.push_back(to_string(x));sort(str.begin(),str.end(),[](const string& a, const string& b){return a+b > b+a; //升序});string res;for(auto& s : str) res += s;if(res[0] == '0') res = "0";  //說明最大的數就是0，此時需要處理前置0return res;}
};

注意比較規則不能使用 >= ，在本題會報錯，我們直接使用大于也是一樣的效果，因為如果相等交不交換都一樣。

4?擺動序列

https://leetcode.cn/problems/wiggle-subsequence/

題目解析：給定一個數組nums，要求我們找到最長的擺動序列的長度。擺動序列我們在動態規劃中有所接觸了，就是子序列中的相鄰元素的關系在大于和小于關系交替出現，而這樣的序列我們畫出折線圖其實就是一個擺動的折線，一上一下交替進行。

我們可以將nums 的數據在圖中畫出來，以便查找規律來總結貪心策略。

假設nums = [1,7,4,9,2,5] ，我們能夠發現在圖中所有的點都構成一上一下的關系，所以整個數組就是最長的擺動序列。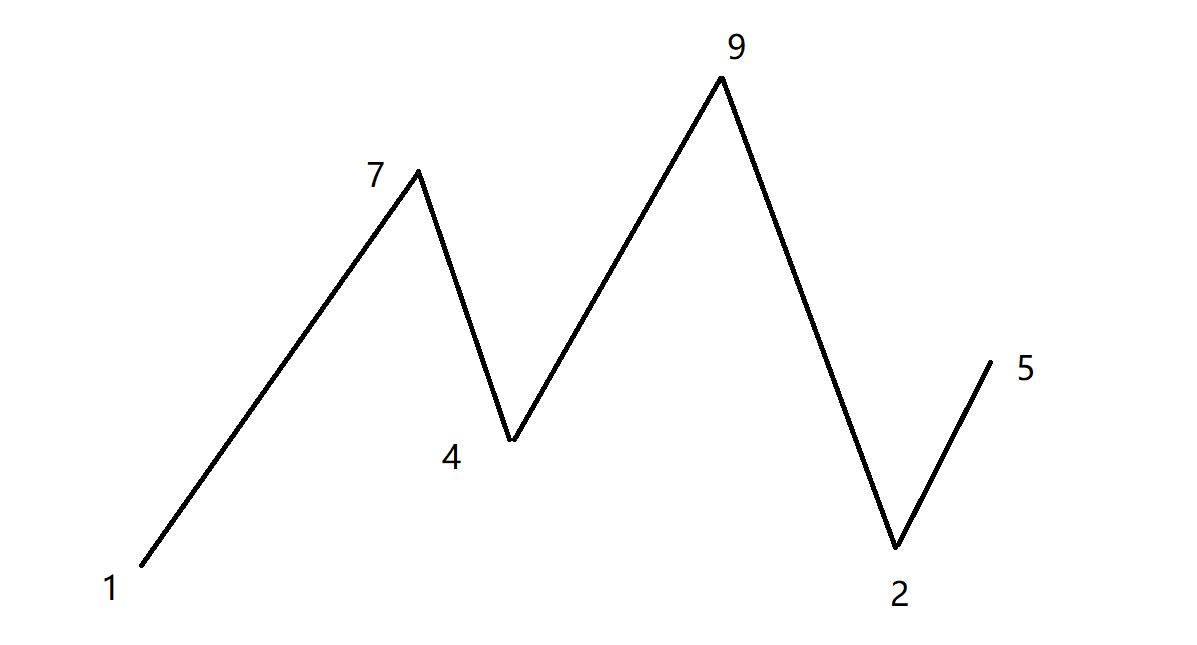

再比如：nums = [1,17,5,10,13,15,10,5,16,8]

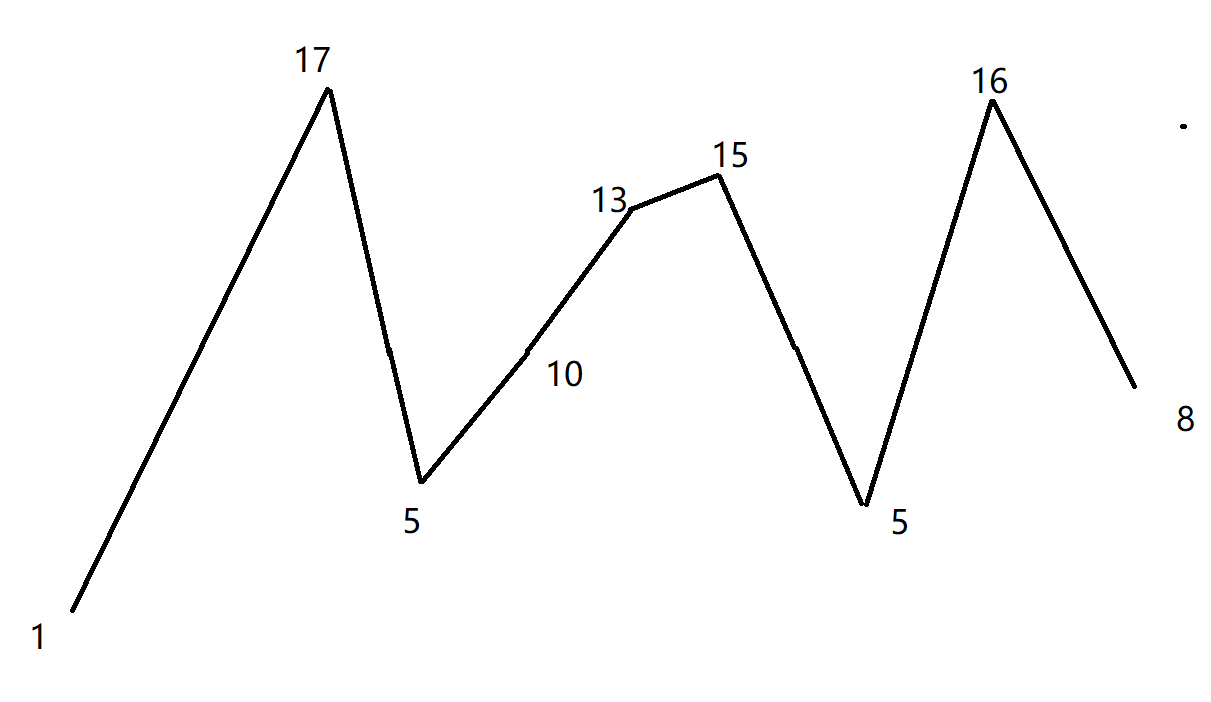
在這個折線圖中如何找到最長的擺動序列呢？很簡單，我們從第一個點開始，如果第一條線是下降趨勢的，那么我們先找到下降趨勢的最低點，如果是上升趨勢的，那么我們先找到上升趨勢的最高點，來作為擺動序列的第二個點。這就是我們的貪心策略。

就比如在 [5,10,13,15]這一段上升區間內，我們會選擇最大的點也就是15，我們找的點越大，那么后續的值小于該點的概率就越大，那么就越有可能構建更長的擺動序列。

比如有 [5,10,13,15,14] ，如果我們選擇10或者13作為上升區間的終點的話，那么后續的14就無法拼接到擺動序列后面，但是如果選擇最大的15，我們就能夠將14拼接到15后面組成擺動序列。同時如果后面是一個較小的值，比如x，如果我們選擇10，能和x構成下降趨勢的話，那么比10更大的15也一定能夠和x構成擺動序列。

給定的nums也有可能會出現連續的相等區間，也就是一條和x軸平行的線，此時我們不需要關系這段區間，而是根據前面不相等區間的趨勢來看，比如 [10，9，9，9，11]，那么我們會將因為10和最前面的9構成下降趨勢，我們會進行記錄，而連續相等的9我們不會修改記錄的趨勢，直到9和11我們才會比較這兩個元素得出是上升趨勢，那么此時需要將下降趨勢的最后一個位置納入到擺動序列中。

那么我們轉換一下題意，可以理解為在nums的折線圖中，找到波峰和波谷的數量，因為我們按照上述貪心策略找到的點，如果將折現看成直線的話，其實就是出現在極值處。

代碼如下：

class Solution {
public:int wiggleMaxLength(vector<int>& nums) {//轉換為找波峰和波谷的數量int flag = 0; //1表示上升趨勢，2表示下降趨勢int res = 1 , n = nums.size();if(n < 2) return n;for(int i = 1 ; i < n ; ++i){//不妨我們直接跳過相等區間if(nums[i] == nums[i-1]) continue;else if(nums[i] > nums[i-1]){if(flag == 2){ //說明前面是下降趨勢，而到了i位置變成上升趨勢，此時可以把nums[i-1]選上res++;}flag = 1;}// else if(nums[i] < nums[i-1]){else{if(flag == 1){//說明前面是上升趨勢，而到了i位置變成下降趨勢，此時可以將nums[i-1]選上res++;}flag = 2;}}//走出循環的時候，我們已經將前面的點都算上的，但是還有最后一段趨勢的點沒有算上//比如最后一段是上升/下降，我們需要把最后一個點算上 [1,2,3,3,3,3,3]/[1,2,3,3,2,2,2,2,2]//但是如果nums全是相等元素，那么此時flag==0，此時我們不需要計算最后一個點,[1,1,1,1,1,1]if(flag != 0) res++;return res;}
};

5?最長遞增子序列

https://leetcode.cn/problems/longest-increasing-subsequence/

題目解析：給定一個數組nums，要求我們找出nums中最長嚴格遞增子序列的長度。

我們使用過動態規劃的思路來解決這個問題，使用dp[i]表示以nums[i]為結尾的最長遞增子序列的長度，這時候我們直到以每一個元素為結尾的最長遞增子序列的長度，但是其實我們可以對這個動態規劃的思路進行貪心優化，當遍歷到nums[i]時，如果前面有多個dp[i]相等，多個元素為結尾的最長遞增子序列長度相等，那么我們其實只需要記錄這些nums[i]的最小值，而不需要關心其他的較大值。那么這樣一來，每一個長度的遞增子序列我們只需要記錄一個最小的結尾值就行了。

模擬一遍該過程：nums = [10,9,2,5,3,7,101,18]

遍歷：

初始： len = [INT_MIN]。len[i] 表示長度為i的遞增子序列的最小的結尾元素，預填入一個INT_MIN，表示任意一個數都可以跟在INT_MIN后面構成一個長度為1的遞增子序列。

i == 0?: nums[i] = 10 , 從后往前遍歷len數組，10 > len[0] ，那么10可以跟在INT_MIN的后面構成遞增關系，變成長度為1的遞增子序列，此時由于還沒有已記錄的長度為1的遞增子序列，那么10可以表示成長度為1的遞增子序列的最小結尾元素,len[1] = 10; 此時 len = [INT_MIN,10]

i == 1:nums[i] = 9 ,從后往前遍歷len數組，9 < len[1]，無法跟在現有的長度為1的遞增子序列后面構成長度為2的遞增子序列。9 > len[0] ，那么9可以跟在長度為0的遞增自詡路i額后面構成遞增關系，變成長度為1的遞增子序列，此時我們需要對比 9 和 len[1] ，來更新所有長度為1的子序列的最小結尾元素， len[1] = min(len[1] , nums[i])，那么此時 len[1] = 9。此時len = [INT_MIN,9]

i == 2:nums[i] = 2,還是按照一樣的思路，從后往前遍歷len，len[1] > 2 , 所以2無法構成更長的遞增子序列。? 2 > len[0] ，2可以跟在長度為0的遞增子序列后面構成長度為1的遞增子序列，此時len[1] = min(2,len[1]) 。此時 len = [INT_MIN,2]

i == 3:nums[i] = 5 。從后往前遍歷len數組，len[1] < 5，那么說明5可以跟在長度為1的遞增子序列后面構成長度為2的遞增自序列，len.push_back(5)。 len[0] < 5 ，此時5也可以跟在長度為0的遞增子序列后面構成長度為1的遞增子序列,len[1] = min(len[1],5)，此時len = [INT_MIN,2,5]。

依此類推，我們就能夠記錄所有存在的遞增子序列的長度所對應的最小的結尾的元素。記錄最小的結尾元素就是我們的貪心策略，因為只要我們的值大于該最小的結尾元素，就能夠拼接到該遞增序列后構成新的遞增序列。

細節：我們對比的是nums[i] 和 len[j] ，但是更新的缺失 len[j+1]，因為是將nums[i]拼接在了長度為j的子序列后面，構成的是長度為j+1的子序列。\

這樣做的話，我們再計算nums[i]是否能夠拼接到nums[j]后面時，動態規劃需要遍歷i次，而貪心策略則只需要遍歷len.size()次，而len.size() <= i。

代碼如下：

class Solution {
public:int lengthOfLIS(vector<int>& nums) {vector<int> len;len.push_back(INT_MIN);for(auto x:nums){//首先對比最長的遞增子序列的結尾元素，看能不能構成更長的長度if(x > len.back()) len.push_back(x);for(int j = len.size() - 2 ; j >= 0 ;--j){ //而后續對比的時候，不需要對比len的最后一個元素，所以從sz-2開始if(x > len[j]) len[j+1] = min(len[j+1],x);}}return len.size() - 1; //len[i] 表示長度為i，那么最大的下標就是最大的長度}
};

本題還可以繼續優化：去掉len[0] 的INT_MIN，len數組中只記錄每個長度的最小結尾元素，基于len數組的形成過程，len數組一定是非遞減的數組，那么我們只需要在len數組中第一個大于等于nums[i]的元素len[j]，然后更新len[j] = nums[i]就行了。為什么呢？首先len的[0,j)區間都是小于nums[i]的，他們后面都能夠跟nums[i]組成新的序列，但是由于他們都比nums[i]小，所以不會更新，到最后，由于len[j-1] < nums[i]，而len[j] >= nums[i] ，所以需要更新。而后面的lem的[j,sz-1]都大于nums[i]，無法拼接nums[i]形成新的嚴格遞增序列。在二分之前需要特殊處理一下nums[i]大于len.back()的情況，此時需要新增位置。

class Solution {
public:int lengthOfLIS(vector<int>& nums) {vector<int> len;len.push_back(nums[0]);//二分優化for(auto x:nums){if(x > len.back()){len.push_back(x);continue;}//找len中大于等于x的左邊界int l = 0 , r = len.size() - 1;while(l < r){int mid = l + (r - l ) / 2;if(len[mid] >= x) r = mid;else l = mid + 1;}len[l] = x;}return len.size();}
};

6?遞增的三元子序列

https://leetcode.cn/problems/increasing-triplet-subsequence/

題目解析：給定一個整數數組nums，要求我們求出是否有長度為3的嚴格遞增數組。

那么本題其實就是上一個題的簡化版本，我們可以直接用上一個題的思路，最后判斷一下len.size()是否大于等于3就行了。

代碼如下：

class Solution {
public:bool increasingTriplet(vector<int>& nums) {vector<int> len;len.push_back(nums[0]);for(auto x : nums){if(x > len.back()){len.push_back(x);continue;}int l = 0 , r = len.size() - 1 ;while(l < r){int mid = l + (r - l) / 2;if(len[mid] >= x) r = mid;else l = mid + 1;}len[l] = x;}return len.size() >= 3;}
};

7?最長連續遞增序列

https://leetcode.cn/problems/longest-continuous-increasing-subsequence/

題目解析：給定一個整數數組nums，要求我們找出最長的連續遞增子序列的長度，其實就是找到最長的遞增子數組的長度。

暴力解法我們會去枚舉以每一個元素為起點的遞增子數組，此時需要兩層循環。

而使用貪心優化，對于 nums[i]，我們找到他的遞增子數組的結尾為 j ，那么[i,j]區間內，以x(x>=i&&x<=j)為起點的最長遞增子數組都是這個區間的一個子區間，那么我們其實只需要記錄一下以i為起點的遞增子數組的長度就行了，后續的(i,j]為起點都不需要枚舉了。

代碼如下：

class Solution {
public:int findLengthOfLCIS(vector<int>& nums) {int n = nums.size(),res = 1;for(int i = 0 ; i < n ; ++i){int j = i + 1;for(; j < n && nums[j] > nums[j-1]; ++j);//此時[i,j)為遞增區間res = max(res , j - i);//貪心i = j - 1; //i下一次以j為起點進行枚舉}return res;}
};

8?買賣股票的最佳時機

https://leetcode.cn/problems/best-time-to-buy-and-sell-stock/

題目解析：給定一個數組prices表示每一天股票的價格，我們需要在某一天買入一個股票，然后在未來的某一天賣出股票，也就是只能完成一筆交易，返回能獲取的最大價值。

當我們在第i天買入股票后，我們會選擇在哪一天賣出呢？？當然是第i天之后的價格最高的一天，這樣我們才能獲取到最大的差價也就是利潤，但是這也有一個前提就是后面的最高價格要比當前價格高，否則不管怎么賣都是虧本的。

那么如何快速找到第i天之后的最高價格呢？我們可以從后往前遍歷數組，記錄最大的后綴價格。

代碼如下:

class Solution {
public:int maxProfit(vector<int>& prices) {int n = prices.size() , res = 0;int maxp = prices[n-1];for(int i = n - 2 ; i >= 0 ; --i){res = max(res , maxp - prices[i]);maxp = max(prices[i] ,maxp);}return res;}
};

9?買賣股票的最佳時機 II

https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-ii/

題目解析：給定每天的股票價格，我們可以交易任意多次，但是手上最多同時持有一個股票，返回能夠獲取的最大利潤。

如果我們將價格化成折線圖，那么我們就很容易能夠得到，最大利潤就是在每一個波谷買入，然后在波峰賣出。但是由于本題不會限制交易次數，我們可以將波谷到波峰這段上升的折現分成多段，每一天如果價格比前一天高，那么我們就在前一天買入今天賣出。

代碼如下：

class Solution {
public:int maxProfit(vector<int>& prices) {int n = prices.size() , res = 0;for(int i = 1 ; i < n ; ++i){if(prices[i] > prices[i-1]) res += prices[i] - prices[i-1]; } return res;}
};

10?K 次取反后最大化的數組和

https://leetcode.cn/problems/maximize-sum-of-array-after-k-negations/

題目解析：給定一個整數數組，我們可以對數組的某一個元素進行取反操作，我們需要返回在進行了k次取反操作之后的最大的數組和。

要使數組和最大，我們該如何規劃這些取反操作呢？首先，如果數組中有負數，我們肯定是優先對負數進行取反，同時再對負數取反的時候也是盡可能先對絕對值大的負數取反。

如果我們將所有負數都轉換為正數之后，還剩下x次取反操作沒有用，那么此時如何做呢？因為我們當前已經是最大的數組和了，再進行取反操作要么數組和不變，要么就會減少了。如果剩下的操作次數x是偶數，那么我們可以對某一個數進行x次取反操作，偶數次取反之后還是原數據，那么數組和不變。如果x是奇數，那么我們將其中的偶數次都對同一個數操作之后，最后剩下一次取反操作我們可以將其用在絕對值最小的那個數上，這樣對數組總和的影響最小。

代碼如下：

class Solution {
public:int largestSumAfterKNegations(vector<int>& nums, int k) {//用堆來存儲負數priority_queue<int> pq;int minabs = abs(nums[0]) , sum = 0;for(auto x : nums){sum += x;minabs = min(minabs,abs(x)); //找到最小的絕對值以便后續剩余奇數次操作時使用if(x < 0) pq.push(-x);}while(pq.size() && k > 0){  //進行k次負數的取反操作sum += 2*pq.top(); pq.pop();--k;}if(k % 2 == 1) sum -= 2 * minabs;return sum;}
};

11?按身高排序

https://leetcode.cn/problems/sort-the-people/

題目解析：給定一個name數組表示每個人的名字，以及一個heights數組對應每個人的身高，要求我們按照身高降序排序返回對應的名字。

本題就是一個簡單的排序問題，我們需要按照題目意思確定排序規則，題目明確了是需要按照身高來對名字進行降序排序。而本題的難點就在于，我們要對名字數組進行排序，但是當名字數組的順序發生變化時，我們無法找到對應名字的身高了，因為他們的下標相等的關系已經被破壞了。

最簡單的我們可以創建一個新的數組，vector<pair<string,int>> 將名字與身高綁定在一起，排序的時候根據身高進行排序就行了。

第二種方法就是利用身高的唯一性，我們可以使用哈希表映射每一個身高對應的名字，然后直接對身高進行降序排序之后找到對應身高的名字就行了，。

還有一種方法就是： 下標數組。我們不對name數組本身排序，而是對每一個name對應的原始下標按照身高進行排序。下標數組適用于排序，但是不改變數據原始位置的情況，而是對下標數組進行排序。

我們首先需要創建一個下標數組，比如例1 的names =?["Mary","John","Emma"]，下標數組就是index = [0,1,2] ，他們對應的身高是heights =?[180,165,170] ，那么我們如何對下標數組排序呢？我們的下標數組存儲的雖然是下標，但是這些下標可以找到對應的人name[index[i]]，也可以找到該下標對應的人的身高heights[index[i]]。而題目要求我們按照身高進行降序排序，那么我們這里的下標就是一個身高的意義，index[i]實際代表的是 heights[index[i]] ，我們排序的時候根據heights[index[i]]的大小關系排序就行了。

代碼如下：

class Solution {
public:vector<string> sortPeople(vector<string>& names, vector<int>& heights) {int n = names.size();vector<int> index(n);for(int i = 1 ; i < n ; ++i) index[i] = i;sort(index.begin(),index.end(),[&heights](const int& i1 , const int& i2){return heights[i1] > heights[i2];});//下標數組按照身高降序排序之后，每一個下標去對應原始name數組的名字vector<string> res(n);for(int i = 0 ; i < n ;++i){res[i] = names[index[i]];}return res;}
};

12?優勢洗牌

https://leetcode.cn/problems/advantage-shuffle/

題目解析：給定兩個數組，我們可以對nums1進行任意排列，使得盡可能多的下標滿足 nums2[i] >?nums1[i]，返回其中一種nums1的排列。

本題其實就是類似于田忌賽馬的問題，齊王和田忌都有上等馬中等馬和下等馬，齊王的上等馬比田忌的上等馬好，齊王的中等馬比田忌的中等馬好，但是比不上田忌的上等馬，齊王的下等馬比田忌的下等馬好，但是比不上田忌的中等馬，我們可以讓田忌的中等馬去贏下齊王的下等馬，用田忌的上等馬去贏下齊王的中等馬，而下等馬則輸給齊王的上等馬，那么田忌還是能夠三局兩勝。

田忌賽馬的本質其實就是一種廢物利用，田忌的下等馬既然是必輸的，那么我們就讓他去消耗掉齊王的最厲害的馬。要使得贏得數量盡可能多，那么我們就需要將齊王的最弱的那一些馬贏了，而齊王的強壯的馬則使用我們的弱的馬去輸掉。

對于本題也是一樣的，我們可以將nums1和nums2排升序，排完序之后，我們從小到大遍歷nums1，當nums1[i]能贏下當前nums2[l]的最弱的數據的時候，那么讓nums1[i] 去對決nums2[l]，如果贏不了，那么就讓nums1[i]去與nums2當前最大的數nums2[r]去比較，廢物利用。

這樣遍歷完之后，nums1的前半段都能贏下nums2，后半段雖然都輸給了nums2，但是我們已經將能贏的都贏下了。

但是現在的問題就是：當我們對nums2排序之后，數據的位置就發生變化了，不再是原始的nums2的順序了，而題目要求返回的是nums1去跟nums2的原始數據一一對決。

那么在本題中，對nums1排序可以直接排，但是對nums2排序的時候，為了不影響原始數據的位置，我們需要使用下標數組來排序。

代碼如下：

class Solution {
public:vector<int> advantageCount(vector<int>& nums1, vector<int>& nums2) {int n = nums1.size();sort(nums1.begin(),nums1.end());//nums2排下標數組vector<int> index(n);for(int i = 1 ; i < n ; ++i) index[i] = i;sort(index.begin(),index.end(),[&nums2](const int& i1 ,const int& i2){return nums2[i1] < nums2[i2];});//排完序之后進行田忌賽馬vector<int> res(n);int l = 0 ,r = n-1; //l表示nums2剩下的的最弱的，也就是 nums2[index[l]],r表示nums2剩余的最強的，也即是nums2[index[r]]for(auto& x : nums1){if(x <= nums2[index[l]]) res[index[r--]] = x; //去對決最強的nums2[index[r]]else res[index[l++]] = x; //能贏下最弱的。去打最弱的 nums2[index[l]]}return res;}
};

13?最長回文串

https://leetcode.cn/problems/longest-palindrome/

題目解析：給定一個字符串，我們可以從字符串中挑選任意字符，來構成回文串，返回能夠構成的最長回文串的長度。

回文串的構造其實很簡單，只需要在原始回文串的兩端各加上一個相同的字符就行了。

那么我們可以先遍歷一遍字符串，將所有的字母的個數統計一下，而對于每一個字符，如果他的個數為x>2，那么我們可以將 x/2個該字符添加到當前回文串的左邊，將x/2個字符添加到當前回文串的右邊，仍然滿足回文串的性質。

最后需要注意的是，回文串長度可以為奇數，最中間的那個字符不需要相等關系，那么我們再拼接完長度為偶數的回文串之后，如果還有字符剩下，那么可以將一個字符加入到回文串的最中間，使得長度再加一。

代碼如下：

class Solution {
public:int cnt[128]; //記錄每一個字符的個數int longestPalindrome(string s) {for(auto ch : s) cnt[ch]++;int n = s.size() , res = 0;for(int i = 'a' ; i <= 'z' ; ++i){if(cnt[i] >= 2) res += cnt[i]/2*2;  //將偶數個字符添加到回文串}for(int i = 'A' ; i <= 'Z' ; ++i){if(cnt[i] >= 2) res += cnt[i]/2*2;}if(res < n) ++res;return res;}
};

14?增減字符串匹配

https://leetcode.cn/problems/di-string-match/

題目解析：給定一個長度為n的匹配字符串，要求我們使用0~n的數字字符組成一個數組，相鄰元素的關系滿足匹配字符串的關系。比如 s[i] == 'D' ，那么 res[i+1] < res[i] ，也就是需要是下降的，如果s[i] == 'I'，那么需要滿足res[i] < res[i+1]，上升趨勢。

那么我們如何進行貪心呢？當我們遇到一段連續的 'I'的時候。由于要連續遞增，那么我們在這段區間的第一個元素要選擇當前剩余的最小的元素，由于這段連續的 'I' 區間的前面一定是一個'D'或者沒有元素，我們在該位置選擇I一定是可行的。

同理，當我們遇到一段連續的'D'區間的時候，我們第一個元素選擇當前的最大的元素。該位置前面要么是連續的'I'遞增區間，要么是沒有元素。那么為什么當前最大的元素一定大于上一個遞增區間的最大的元素呢？因為當我們從前往后按照這樣的規則填下來之后，由于遞增的區間我們是從最小的一部分去選，當填到遞減區間的時候，剩余的元素都是比該遞增區間大的元素，自然可以滿足。

代碼如下：

class Solution {
public:vector<int> diStringMatch(string s) {int n = s.size() , minn = 0 , maxn = n;vector<int> res(n+1);//從前往后找for(int i = 0; i < n ;++i){if(s[i] == 'D'){//找完這段連續D區間int j = i + 1;for(; j < n ; ++j) if(s[j]!='D') break;//此時[i,j)是遞減區間，我們選擇當前的最大值開始填for(int x = i; x < j ; ++x){res[x] = maxn--;}i = j - 1;//下一個從s[j]開始找遞增的區間}//否則就是找遞增區間else{int j = i + 1;for(;j < n ; ++j) if(s[j] != 'I') break;//[i,j)是一段遞增區間，從最小的值開始填for(int x = i ; x < j ; ++x) res[x] = minn++;i = j-1;}}//這樣一趟填下來，我們只填了[0,n-1)區間，還剩下最后一個位置沒填//最后一個位置有兩種情況，一種是s[n-1] =='I'，那么說明這是一段遞增區間的結尾，而我們剩下的數一定是這段遞增區間的最大值+1，而相反如果是'D'，那么剩下的數一定是該遞減區間的最小值-1//還剩下最后一個位置就填剩下的元素就行res[n] = minn;return res;}
};

解法2：

我們用字符串來表示構建的數組，

比如：res = "01234",s = "IDID",我們只需要將下降的區間進行逆置一下就行了，比如s的 [1,1]區間是下降的，那么對應res的[1,2]區間需要是降序的，逆置一下res的[1,2]區間，變成了 res = "02134"，然后s的[3,3]區間是下降的，那么對應res的[3,4]區間是下降的。我們逆置一下res的[3,4]區間，就變成了 res = "02143"。這樣就能夠構建出我們所需的滿足匹配字符串的序列。

上面res為字符串時，只能用于n為0~9時的序列的構建，如果我們將res使用數組來代替，那么就可以進行n為任意長度(不超內存)的序列的構建了。?

為什么這樣能行呢？其實跟貪心的思路一樣，相當于我們在遇到連續的’D‘的區間的時候，還是選取一段比前面的’I’區間大的區間，但是我們逆序排序，在這個思路中選擇的比'I‘區間大的區間則剛好是連續遞增區間的后面一段。

比如：s = 'IIIIDDDIID',第一段長度為4的區間我們選擇[0,3]來升序放置，而后一段長度為3的區間我們會選擇3個元素[4,6]來逆置放置，依次類推。

代碼如下：

class Solution {
public:vector<int> diStringMatch(string s) {int n = s.size();vector<int>res(n+1);for(int i = 0 ; i <= n ; ++i)res[i] = i;for(int i = 0 ; i < n ; ++i){if(s[i] == 'D'){//找連續遞減區間int j = i + 1;for(;j < n ; ++j) if(s[j] == 'I') break;//[i,j)為連續D區間，對應的[i,j]都需要遞減reverse(res.begin() + i , res.begin()+j+1);i = j;}}return res;}
};

15?分發餅干

https://leetcode.cn/problems/assign-cookies/

題目解析：給定孩子的胃口數組 g，以及餅干的大小數組s，每個孩子最多給一塊餅干，同時只有該餅干的大小大于等于孩子的胃口大小時，該孩子才能夠滿足，返回我們最多能夠滿足的孩子的數量。

本題其實還是一個田忌賽馬的問題，為了盡可能滿足多的孩子，那么我們會優先去滿足哪些胃口小的孩子。

我們將孩子的胃口和餅干的大小升序排序。從小到大遍歷餅干的大小，如果當前餅干能夠滿足最小胃口的孩子，那么就給他，如果滿足不了，那么這塊餅干也沒用了，跳過，去拿下一塊餅干比較。

代碼如下：

class Solution {
public:int findContentChildren(vector<int>& g, vector<int>& s) {sort(g.begin(),g.end());sort(s.begin(),s.end());int j = 0 , res = 0 , n = g.size();for(auto x : s){//當前的最小的餅干if(j == n) break ;//說明所有的孩子都滿足了if(x >= g[j]) res++ , j++; //能夠滿足胃口最小的孩子}return res;}
};

16?最優除法

https://leetcode.cn/problems/optimal-division/

題目解析：給定一個整數數組，數組中的每個元素都被用于一個只包含除法和括號的運算式中，我們需要在 n0/n1/n2/n3.... nm 表達式中手動添加任意對括號，使得整個表達式的運算結果最大。

對于一個除法的表達式，比如 a/b/c/d ，我們其實可以將除法的臨時結果使用分數保存，a/b/c/d = a/bcd ，再添加完任意的括號之后，比如我們在(c/d)添加括號，就變成了 a/b/(c/d) = ad/bc。舉這個例子是為了表明，我們的分數之間的除法其實是可以轉換為乘法的, a/b = a*1/b，那么根據這個性質，其實不管我們怎么添加括號，最終結果一定是一個 x/y 的表達式，x為nums中任意個數的乘積，y為nums中其余數的乘積。?

但是根據我們的初始表達式 n0/n1/n2.../nm ，不管我們怎么添加括號，n0 一定是在最終表達式的分子上，同時n1一定是在最終表達式的分母上，或許我們又可以轉換為 n0/n1? * (x/y) 。

要使得最終結果最大，那么就需要讓x盡可能大而y盡可能小，那么我們能否讓除了n0和n1之外的所有的數都在分母上呢？能。因為題目給定了nums中所有元素都是大于等于2的，不會存在負數和小數，我們只需要讓除了n0和n1之外的所有元素都出現在分子，就能夠得到最大的結果。

比如 [1,2,3,4,5,6,7] ，我們能否通過添加括號讓[3,4,5,6,7]都在分子上呢？1/(2/3/4/5/6/7)，這其實就相當于 n0/(n1/n2/n3../nm)，而括號中的表達式根據上面的 a/b/c/d = a/bcd ，就可以轉換為 n0/(n1/(n2*n3*...*nm)) = (n0*n2*n3*n4*...*nm) / n1。

那么我們就只需要在 n1前面加上一個(,同時在最后一個元素后面加上一個)就行了，然后把 / 也添加在字符串中。

特殊情況就是當nums只有兩個元素時，括號是多余的。

代碼如下：

class Solution {
public:string optimalDivision(vector<int>& nums) {string res;int n = nums.size();res += to_string(nums[0]);if(n == 1);else if(n == 2)res += "/" + to_string(nums[1]);else{res += "/(";for(int i = 1 ; i < n ; ++i) res += to_string(nums[i]) + "/";res.back() = ')'; //把最后多出來的 / 替換為 )}return res;}
};

17?跳躍游戲 II

https://leetcode.cn/problems/jump-game-ii/

題目解析：給定一個數組，每一個位置的值nums[0]表示在這個位置起跳一步最多可以跳多遠，要求我們求出從下標0跳到下標n-1所需的最少的步數。

題目保證可以到達n-1，那么其實我們可以把0當成起點，n-1當成終點，來做bfs或者dfs，但是如果直接暴力dfs的話，會有相當多重復遍歷的路徑，除非我們使用記憶化搜索來進行路徑去重。所以本題我們使用bfs更加方便。

class Solution {
public:int jump(vector<int>& nums) {int n = nums.size();queue<int> q;vector<bool> vis(n); int res = 0;vis[0] = true;q.push(0);while(q.size()){//當前q中的節點能通過res步走到，那么通過q中的節點再走一步int cnt = q.size();while(cnt--){int x = q.front();if(x == n-1) return res;q.pop();for(int i = 1 ; i <= nums[x] ; ++i){if(x + i < n && !vis[x + i]) {q.push(x+i); //說明本條是通往x+i的最短路徑vis[i+x] = true;}}}res++;}return res;}
};

同時本題也可以是一個經典的動態規劃問題，定義dp[i]為到達i位置的最少步數就行了，動態規劃就不寫了，很簡單。

在本題中，其實層序遍歷的過程就是從左往右的，所以我們并不需要隊列來模擬，只需要一個dis數組就行了，代碼如下：

class Solution {
public:int jump(vector<int>& nums) {int n = nums.size();vector<int> dis(n,INT_MAX);dis[0] = 0;for(int i = 0 ; i < n ; ++i){for(int x = 1; x <= nums[i] && x + i < n; ++x){if(dis[x+i] > dis[i] + 1) dis[x+i] = dis[i] + 1;}}return dis[n-1];}
};

這種優化之后的層序遍歷在代碼上其實和動態規劃的寫法基本一致。

18?跳躍游戲

https://leetcode.cn/problems/jump-game/

題目解析：本題和上一題類似，但是不保證一定能跳到終點，需要我們自己判斷。

借鑒上一題的優化后的bfs來做就行了。代碼如下：

class Solution {
public:bool canJump(vector<int>& nums) {int n = nums.size();vector<bool> can(n,false);can[0] = true;for(int i = 0 ; i < n ; ++i){if(!can[i]) continue; //無法到達i//走到這里說明能到達i，那么自然能通過i到達后面的點for(int x = 1 ; x <= nums[i] && x + i < n; ++x){can[x+i] = true;}}return can[n-1];}
};

同時本題還有一種更簡單的做法就是：如果我們能夠到達x位置，那么是不是意味著[0,x]都可到達？

比如我們從0位置開始，最遠能夠到達 nums[0]+0，意味著[0,nums[0]]這些位置都可以到達，然后我們去遍歷nums[1]~nums[nums[0]] 這些點能夠到達的最遠位置maxn，那么又可以延伸到 [0,maxn]都可到達，那么我們只需要這樣遍歷完nums或者遍歷到maxn，如果maxn大于等于n-1說明能夠到達n-1。

代碼如下：

class Solution {
public:bool canJump(vector<int>& nums) {int maxn = 0, n = nums.size();for(int i = 0 ; i <= maxn && i < n ; ++i){maxn = max(maxn,i + nums[i]);  //能到達的最遠距離}return maxn >= n-1;}
};

19?加油站

https://leetcode.cn/problems/gas-station/

題目解析：有一條環路，環路上有n個加油站，gas[i] 表示第i個加油站可以加的油量，而cost[i]則表示從加油站i到加油站i+1需要消耗的油量。我們需要判斷能否以某一個加油站為起點，沿著環路走一圈，如果能，返回起點加油站的編號，不能就返回-1.

本題其實有兩個遍歷，可加油量和消耗量，假設我們到達第i個加油站時，剩余油量為 x，此時x一定是大于等于0的，那么我們在加油站i加 gas[i] 的油，同時走到第i+1個加油站需要cost[i] 的油，那么到達第i+1個加油站時的剩余油量為 x + gas[i] - cost[i] ，但是這個剩余油量可能會小于0，如果小于0，則說明無法到達第i+1個加油站。

如果我們暴力來解決的話，那么直接枚舉每一個加油站為起點，然后看能否走一圈，但是這樣會超時，我們可以進行以下優化：

假設我們從第i個加油站出發，能夠走到第j個加油站，那么說明，我們從第i個加油站出發時，到達[i,j]這些加油站時，剩余油量都是大于等于0的。但是如果我們無法到達[i,z] ，此時既然已經枚舉到了z，那么說明z-1是可以到達的，而無法從z-1到達z。那么我們繼續枚舉i+1為起點看能否到達加油站z。

由于我們前面枚舉了i為起點能夠到達i+1，那么從i到達i+1時的剩余油量一定是x >= 0 的，也就是說從i出發前往z的總油量一定是大于等于從i+1出發前往z的總油量的，而從i出發都無法到達z，那么從i+1出發也一定無法到達z。

所以當我們枚舉起點i無法到達加油站z時，[i+1,z-1]這些加油站為起點也一定無法到達z，那么下一次直接從z加油站為起點判斷能否繞一圈。

代碼如下：

class Solution {
public:int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {int n = gas.size() , i = 0;//枚舉起點while(i < n){//從i出發最遠能夠到達哪個加油站int res = 0 , x = 0; //res剩余油量,x為能走的步數for(; x < n && res >= 0; ++x) {res += gas[(i+x)%n] - cost[(i+x)%n]; //走到i+x+1加油站時剩余的油量，也就是說能走x+1步}if(res >= 0) return i; //說明以i為起點，走了n-1步了，繞了一圈還有剩余的油else i += x; //無法走到i+x,也就是只能走到[i,i+x]，下一次直接枚舉從i+x出發}return -1; }
};

20?單調遞增的數字

https://leetcode.cn/problems/monotone-increasing-digits/

題目解析：給定n，返回小于等于n的最大的單調遞增的數字。單調遞增的數字意思就是，對于每一對相鄰的數位，左邊的高位的數字小于等于右邊的低位的數字。

比如 n = 1231，那么最大的單調遞增數字就是1111，比如n=1100，那么最大的單調遞增數字就是1229。

其實小于等于n的數字有兩類，一類是和n位數相同的，一類是位數小于n的，那么我們肯定是優先考慮位數和n相同的那一類數字。

假設n的每一位是 :? numN[ ]? ，而我們要找的數字的每一位是 numRes[ ] ，而既要位數和n相同，同時小于等于n，那么對于numRes，我們從前往后對比res和n的每一位，如果numN[i] == x , 那么我們要使得res盡可能達，res的第i位要填多少呢？肯定是盡可能大的填，我們就填x。

比如n = 1231 ，我們首先會將res填成 numRes = [1,2,3, ] ，當遍歷到n的最后一位時，numN[i] = 0 < numRes[i-1] ，那么此時我們的res的第i位就不能填n的第i位了，因為這樣一來res就不是單調遞增數字了，那么我們怎么做呢？此時需要向前借位，也就是讓前面的數變小一點。

我們首先向前遍歷到 3，能否在3借位呢？能，因為在3借1位之后變成2，2>=numRes[1]

而當我們將3改成2之后，后續在本位res就已經小于n了，那么后續的位不管再大，整體也是小于等于n的，那么我們可以直接將后續的所有位都改為9.

于是我們就改成了 numRes = [1,2,2,9]。

又比如 n = 1100 ，我們首先填numRes = [1,1, ,]，填到第3位時我們發現無法填0，那么向前借位，最終借到了最高位，將最高位改為0之后，后續都改為9，就變成了 numRes = [0,9,9,9]。

為了方便操作，我們可以先將n轉化為字符串進行操作。

代碼如下：

class Solution {
public:int monotoneIncreasingDigits(int n) {string res = to_string(n);int len = res.size();for(int i = 1 ; i < len ; ++i){ //直接從第1位開始看if(res[i] < res[i-1]){//說明比前一位小，需要借位char ch = res[i];int j = i - 1;for(;j > 0 ; --j){ //看第j位能否修改成chif(res[j-1] < res[j]) break; //說明在第j位借1之后還是單調遞增}res[j++]--; //在第j位借位，只需要第j位減1就行了for(;j < len ; ++j) res[j] = '9';break;}} return stoi(res);}
};

21?壞了的計算器

https://leetcode.cn/problems/broken-calculator/

題目解析：給定一個計算器，只能執行乘2和減1兩種操作，求出從startValue到target的最少的操作次數。

如果我們直接按照題目意思來模擬的話，從貪心的角度來看，我們需要讓startValue盡可能快的接近或者超過target，那么我們會優先使用乘2操作，當startValue大于target之后就使用減法得到target。

但是這種貪心并不是最優解，比如：2 - > 6 ，如果我們使用貪心來做，那么會先乘2次變成8，再減2兩次變成6，此時一共需要4次操作，但是最優解是 2->4->3->6，此時只需要三次操作。

為什么貪心策略不是最優解呢？因為當我們得出startValue大于target之后，此時來進行減1操作，如果減1的次數大于2，那么一定是不如在本次乘2之前進行一次減1，減完1之后再去乘2的，如果減1的次數大于4，那么就不如在倒數第二次乘2操作之前先進行一次減1操作再來進行兩次乘2操作。?

但是我們可以進行逆向思維，我們求出最快由target得到startValue的方法，就相當于求出了最快由startValue得到target的方法。不過此時我們的操作就變成了除2操作和加1操作，同時除2操作的前提是偶數。

那么此時如何進行貪心呢？我們要讓target盡快變成startValue，那么優先選擇除法，但是除法的前提是偶數，如果不是偶數，那么只能選擇加法。

那么如何證明先除后加比先加后除快呢（或者說如何證明先將target除到小于startValue再去執行加法會比一邊執行加法一邊進行除法快呢）？很簡單，比如從x除法，我們需要得到x/2+1，先除后加只需要兩次操作，而先加后除需要3次操作，因為除之后的加法，一次加1可以等價于除之前的兩次加法，這樣一來我們就能得到最少的操作次數。

代碼如下：

class Solution {
public:int brokenCalc(int startValue, int target) {int res = 0;while(target > startValue){res++;if(target % 2) target++;else target /= 2;}//此時target小于等于startValue，還需要執行 startValue - target 次加一操作res += startValue - target;return res;}
};

22?合并區間

https://leetcode.cn/problems/merge-intervals/

題目解析：給定一個n*2 二維數組表示n個區間，要求我們合并其中重疊的區間，合并完之后返回。

比如給定三個區間 [1,4] , [4,7] 和 [2,3] ，我們就需要合并為[1,7] 來返回。

如果給定的是: [1,2] [3,4] , 這兩個區間沒有重疊部分，不需要合并，返回[1,2],[3,4]。

那么現在的問題就變成了如何進行有重疊部分的區間的合并。

什么情況下兩個區間有重疊部分呢？假設兩個區間 [a,b] 和 [c,d] ，如果 c <= b 或者 a <= d ，那么這兩個區間就是有交集的。?

而如果我們能夠確保區間 [a,b] 和 [c,d] 中 a<=c ，那么我們只需要判斷 b >= c 就能夠確定這兩個區間是有重疊部分了，那么合并之后的區間是：? [a,max(b,d)] 。合并之后，我們會接著去判斷下一個區間 [e,f]是否和 [a,max(b,d)] 有重疊。

那么現在的問題就是我們如果暴力來判斷的話，就需要兩層for循環來枚舉每一對區間是否有重疊部分，這樣時間復雜度過高，如何優化呢？

很簡單，我們可以先對所有區間以區間的左端點進行升序排序，這樣一來，所有有重疊部分的區間就都是連續的了。

因為當我們求出了當前合并區間的右端點為 x , 下一個區間的左端點一定是越小越好，假設下一個區間的左端點為 y > x ,那么說明下一個區間與當前區間沒有交集，后面的所有區間左端點都在下一個區間的右邊，那么自然也不會和當前區間有交集，也就說明本區間已經合并完成了。?

代碼如下：

class Solution {
public:vector<vector<int>> merge(vector<vector<int>>& intervals) {sort(intervals.begin(),intervals.end()); //以左端點進行升序排序vector<vector<int>> res;int begin , end , n = intervals.size();if(n == 1) return intervals;for(int i = 0 ; i < n;){//找與當前區間有重疊部分的區間begin = intervals[i][0] , end = intervals[i][1];int j = i + 1;for(;j < n; ++j){if(intervals[j][0] > end) break;end = max(end , intervals[j][1]);}//走到這里說明intervals[j]與當前區間沒有交集了，當前區間已經合并完，或者j==n了res.push_back({begin,end});i = j; //}return res; }
};

23?無重疊區間

https://leetcode.cn/problems/non-overlapping-intervals/

題目解析：給定多個區間，我們需要移除某些區間，使得剩余的區間沒有重疊部分，返回最少需要移除多少個區間。

首先本體的區間重疊和上一題有不同的地方，上一題的區間只要有一個點從重疊了那么就算重疊，而本題只有一個點重疊不算重疊。

還是一樣的，我們需要現將所有區間以左端點進行排序，使得所有可能存在重疊部分的區間相鄰，然后再去考慮刪除區間。

對于兩個區間 [a,b] [c,d] 其中 a <= c ，如果我們發現 c < d , 那么此時這兩個區間有重疊，我們需要移除其中一個來避免重疊，選擇哪個區間進行移除呢？ 移除右端點較大的區間。從貪心的角度來講，既然[a,b]和[c,d]需要移除一個，同時也要盡可能避免剩下的那個區間和后面的區間不會有重疊，那么就需要保證剩下的那個區間的右端點盡可能小，所以我們需要移除右端點較大的區間。

代碼如下：

class Solution {
public:int eraseOverlapIntervals(vector<vector<int>>& intervals) {sort(intervals.begin(),intervals.end());//左端點升序排序int res = 0;int end = INT_MIN, n = intervals.size();for(int i = 0 ; i < n ; ++i){if(intervals[i][0] < end){//有重疊，此時需要刪除右端點大的區間end = min(end , intervals[i][1]);res++;}else {end =intervals[i][1]; //去判斷后續區間是否有重疊}}return res;}
};

24?用最少數量的箭引爆氣球

https://leetcode.cn/problems/minimum-number-of-arrows-to-burst-balloons/

題目解析：本題給定一些氣球所處的位置，我們只需要關注x坐標，后續我們射箭的時候是沿著 x軸的垂直方向射箭。只要滿足我們射箭的位置 x = a ,a在氣球的 [xstart,xend] 內部，這根箭就能引爆氣球。求出最少需要射多少次箭才能引爆所有氣球。

我們需要射箭的次數盡可能小，那么一次射箭就需要盡可能引爆更多的氣球，那么什么情況下我們一根箭能夠引爆多個氣球呢？假設兩個氣球的直接范圍為 [a,b] 和 [c,d] ，那么只要這兩個氣球在x軸看有交集，那么我們就能在這個交集內射一根箭同時引爆這兩個氣球。假設 a<=c,那么如果 c<=b，就說明這兩個氣球有交集，那么交集在哪呢？? [c,min(d,b)]。

那么如何判斷一根箭能否引爆3個氣球呢？比如 [a,b] [c,d] [e,f] (a<=c<=e)，如果前兩個氣球有交集[c,min(b,d)]，那么第三個氣球如果和 [c,min(b,d)] 有交集，就說明可以一次性引爆這三個氣球。

本題其實就是類似于求有重疊區間的交集。同樣我們還是需要將有重疊部分的區間放在一起，以左端點升序排序。代碼如下：

class Solution {
public:int findMinArrowShots(vector<vector<int>>& points) {sort(points.begin(),points.end());int end, n = points.size() , res = 0;for(int i = 0 ; i < n ;){//求出一次最多能夠引爆的數量end = points[i][1];int j = i + 1;for(;j < n ; ++j){if(points[j][0] <= end){end = min(end , points[j][1]);}else break;}res++;i = j;}return res;}
};

25?整數替換

https://leetcode.cn/problems/integer-replacement/

題目解析：給定一個正整數n，如果n為偶數我們需要對其進行/2操作，如果n為奇數，可以對其進行加一或者減一操作。返回將n變為1的最少的操作次數。

本題我們可以使用動態規劃來解決，也可以使用dfs+記憶化來解決。記憶化搜索的代碼如下：

class Solution {
public:unordered_map<long long , int> hash; //記憶化hash[x]記錄將x變為1的最少操作次數int integerReplacement(int n) {return dfs(n);}int dfs(long long n){if(n == 1) return 0;if(hash.count(n))return hash[n];if(n % 2){hash[n] = 1 + min(dfs(n+1) , dfs(n-1));}else{hash[n] = 1 + dfs(n/2);}return hash[n];}
};

本題也可以使用貪心策略來做，我們可以思考一下哪一種操作能夠更快使n變為1呢？當然是/2操作，但是/2操作的前提是n為偶數，偶數進行除2的操作，從二進制角度來看，其實就是右移一位的操作。而當n為奇數時，有加一和減一兩種操作，哪一種操作更優呢？更優其實就是要讓后面能夠進行更多的/2操作。

我們可以拿出n的二進制位來看，如果n為奇數，那么n的二進制序列的最低位一定是1，而我們不管是加一還是減一，都是讓最后一位變為0，好讓我們能夠執行偶數的二進制的右移一位操作(除2)的操作。我們可以拿出最后兩位來看，如果最后兩位是 01 ，那么此時我們如果執行+1操作，那么就變成了10，那么本次加一之后，下一次執行除2操作，除2之后又變成了奇數，又需要進行加一或者減一的操作，。而如果我們進行減一操作，那么就變成了00，然后執行除2操作，右移一位之后，最低為仍然是0，那么我們可以接著進行除2操作，就可以省去了一次減一或者加一的操作。而如果n的最后兩位為01，那么此時我們執行減一操作更加好。

其實我們也可以想到，我們需要執行的/2的操作次數其實和n的二進制的最高位的1有關系，除2操作的總次數其實就是最高位1的位置，那么我們就需要盡量讓中間過程的加一和減一的操作次數少一點。?

代碼如下：

class Solution {
public:int integerReplacement(int n) {int res = 0;while(n != 1){if(n % 2 == 0){n = n/2;res++;}else if(n % 4 == 1){ // 01n = n-1;res++;}else { //11n = n/2+1; //n++可能溢出，可以直接走兩步 n = (n + 1) / 2 = n/2 + 1; 因為此時n是奇數res += 2;}}return res;}
};

此時我們會發現一種特殊情況就是n==3的時候，+1是不如減1操作的，因為此時更高高位已經沒有1了，減一之后只需要執行一次除2操作就變成了1，所以n==3的時候特殊判斷一下。

class Solution {
public:int integerReplacement(int n) {int res = 0;while(n != 1){if(n == 3){ res += 2; return res;}if(n % 2 == 0){n = n/2;res++;}else if(n % 4 == 1){ // 01n = n-1;res++;}else { //11n = n/2+1; //n++可能溢出，可以直接走兩步 n = (n + 1) / 2 = n/2 + 1; 因為此時n是奇數res += 2;}}return res;}
};

26?俄羅斯套娃信封問題

https://leetcode.cn/problems/russian-doll-envelopes/

題目解析：給定一組信封的大小(長和寬)，對于兩個信封，如果一個信封的長和寬都小于另一個信封，那么該信封可以放進另一個信封里面去。要求我們返回這些信封最多能夠有多少個套在一起。

本題的常規解法還是動態規劃，動態規劃之前需要先對信封以長度或者寬度進行升序排序，dp[i]表示以第i個信封作為最外層信封時，最多套娃的信封數量。再求dp[i]的時候，我們需要遍歷[0,i-1]找出能夠裝進i中的信封j,dp[i] = max(dp[j]+1)，時間復雜度為O(N^2)，代碼如下：

class Solution {
public:int maxEnvelopes(vector<vector<int>>& envelopes) {sort(envelopes.begin(),envelopes.end());int n = envelopes.size() , res = 0;vector<int> dp(n,1);for(int i = 1; i < n ; ++i){for(int j = 0 ; j < i ; ++j){if(envelopes[i][1] > envelopes[j][1] && envelopes[i][0] > envelopes[j][0]) dp[i] = max(dp[j]+1 , dp[i]);}res = max(res,dp[i]);}return res;}
};

這種暴力的動態規劃會超時，那么如何快速求出dp[i]呢？我們在排序的時候，是根據長來進行升序排序的，假設不存在相同的長，那么我們其實可以把高單獨拿出來，作為一個序列，[a,b,c,d] ，由于這個序列的信封的長已經是嚴格遞增了，那么只需要高也嚴格遞增，那么就是能夠進行套娃的。比如 (1,2) (2,3) (3,2) (4,6) ,把高拿出來就是 [2,3,2,6]，那么我們要求最多能夠套娃的數量，其實就是再求一個高度的嚴格遞增序列的最大的長度。比如上面的最長遞增序列就是 [2，3，6]，所以最多能夠套娃3個信封。

但是本題的長可能相同，此時我們默認的排序規則就是長相同的情況下按照高的升序排序，那么我們求得最長遞增子序列中，就有可能會包含長度相等的信封，此時是不對的。如何避免長度相同的信封出現在一個遞增子序列中呢？很簡單，我們排序的時候，讓長度相同的信封，按照高度的降序排序，那么我們在選擇遞增子序列的時候，就不會選到兩個長度相同的信封了，因為只要長度相同，兩兩之間的高度都是遞減的。

同時，我們做動態規劃的時候就只需要解決最長遞增子序列就行了。

代碼如下：

class Solution {
public:int maxEnvelopes(vector<vector<int>>& envelopes) {sort(envelopes.begin(),envelopes.end(),[](const vector<int>& v1 , const vector<int>& v2){return v1[0] < v2[0] || (v1[0] == v2[0] && v1[1] > v2[1]); });int n = envelopes.size() , res = 0;vector<int> dp(n,1);//變成了求最長遞增子序列for(int i = 0 ; i < n ; ++i){for(int j = 0 ; j < i ; ++j){if(envelopes[j][1] < envelopes[i][1]) dp[i] = max(dp[i] , dp[j] + 1);}res = max(res,dp[i]);}return res;}
};

但是這樣下來，本質還是一個兩層循環的動態規劃，時間復雜度還是O(N^2)。而我們可以參考前面做過的最長遞增子序列的方法來進行二分的優化。

我們在動態規劃求 dp[i] 的時候，同時維護一個len數組,len[j] 表示在前i個信封中，能夠套娃j個信封的最外層信封的最小的高度，那么這樣一來我們就可以通過二分查找，來優化掉第二層O(N)的循環，二分查找的思路參考本文的第5題。其實這里的len我們并不一定要套著題目來理解，直接理解為在高度的序列中，長度為j的嚴格遞增子序列的最小的末尾元素，此時len數組一定是遞增的，我們可以通過二分查找找到len數組中大于等于第i個信封的高度的最小長度，假設為 len[x] ，那么我們可以將len[x] 更新為 envelopes[i][1]。

class Solution {
public:int maxEnvelopes(vector<vector<int>>& envelopes) {sort(envelopes.begin(),envelopes.end(),[](const vector<int>& v1 , const vector<int>& v2){return v1[0] < v2[0] || (v1[0] == v2[0] && v1[1] > v2[1]); });int n = envelopes.size() , res = 0;vector<int> len;len.push_back(envelopes[0][1]);//變成了求最長遞增子序列for(int i = 1 ; i < n ; ++i){//特殊判斷一下需要增加新長度的時候int h = envelopes[i][1];if(h > len.back()) len.push_back(h);else{//找len中大于等于h的第一個位置int l = 0 , r = len.size()-1;while(l < r){int mid = l + (r - l) / 2;if(len[mid] >= h) r = mid;else l = mid + 1;} len[l] = h;}}return len.size();}
};

27?可被三整除的最大和

https://leetcode.cn/problems/greatest-sum-divisible-by-three/

題目解析：給定一個數組，可以刪除元素，要求我們求出數組和為3的整數倍的最大和。

如果整個數組和為3的整數倍，那么不需要刪除元素，如果不為3的倍數，那么就需要刪除一些元素。要使得剩余元素的和最大，那么就要讓刪除元素的和盡可能小。我們需要從刪除的元素的角度來解決本題，所謂正難則反。

本題需要用到同余定理，也就是 a%p - b%p = (a-b)%p （a>b）.

我們可以把nums的所有元素劃分為三類， {S1,S2,S3}，S1包含所有能被三整除的元素，S2為所有模3結果為1的元素，S3為所有模三結果為2的元素。

求出所有元素的和為sum，如果sum%3==0，那么不需要刪除元素。

如果 sum % 3 == 1 ，那么此時有兩種刪除的策略，刪除S2中最小的元素，或者刪除S3中最小的兩個元素。

如果sum % 3 == 1，此時也有兩種刪除策略，刪除S3中最小的元素或者刪除S2中最小的兩個元素。

我們需要用到S2和S3的最小和次小元素，可以在求和的過程中記錄以下。

代碼如下：

class Solution {
public:int maxSumDivThree(vector<int>& nums) {int sum = 0 , a1 = INT_MAX , a2 = INT_MAX ,b1 = INT_MAX , b2 = INT_MAX;for(auto x : nums){sum += x;if(x % 3 == 1){if(x <= a1) a2 = a1 , a1 = x;else if(x < a2) a2 = x;}else if(x % 3 == 2){if(x <= b1) b2 = b1 , b1 = x;else if(x < b2) b2 = x;}}if(sum % 3 == 1){//兩種策略int del= INT_MAX; //if(a1 != INT_MAX) del = a1; //S1需要有一個元素if(b2 != INT_MAX) del = min(del , b1 + b2); //S2需要有兩個元素sum -= del;}else if(sum % 3 == 2){int del = INT_MAX;if(a2 != INT_MAX) del = a1 + a2;if(b1 != INT_MAX) del = min(del , b1);sum -= del;}return sum;}
};

貪心是求這類問題比較快的方法，同時我們也可以使用動態規劃來求，動態規劃是解決這一類問題的通用方法，定義狀態表示為: dp[i][j] 表示在前i個元素中選，使得和 sum % m?== j 的最大和。而考慮dp[i][j] 的時候可以考慮第i個元素的選和不選，如果不選，則需要找到前i-1個元素中選余數為(j -??nums[i] % m + m )%m的最大和。具體代碼就不在這里實現了。

28?距離相等的條形碼

https://leetcode.cn/problems/distant-barcodes/

題目解析：給定一個數組，數組中的元素的值表示一個條形碼，可能存在多個相同的條形碼，我們需要對所有的條形碼進行排序，使得任意兩個相鄰的條形碼不相同。

其實就是需要我們對元素進行排序，使得相鄰元素不相等。

對于這一類問題有一種很取巧的方式，就是我們先對所有元素進行計數，然后依次放每一類元素，首先放奇數下標，然后放偶數下標。

更具體的，我們先把所有的x拿出來，從下標0開始放，依次放0,2,4,6... i，直到把所有的x放完，然后再拿出下一個元素y，從i+2繼續在偶數下標處放i，以此類推直到放完偶數位置，然后再從奇數下標開始放。

但是這樣做有一種特殊情況就是 : 其中一個元素出現了超過元素總數的一半，(n+1)/2，n為奇數此時我們其實是可以使得所有元素相鄰不相等的，但是可能由于該元素不是第一個也不是最后一個放的，那么這個元素就會橫跨奇數和偶數的下標，同時由于數量過多，到最后一個奇數位置，是和該元素的偶數起始位置相鄰的，那么就出錯了。就比如： [1,2,2,2,3]，如果我們先放1，變成 [1,_,_,_,_] ，然后放2，就會變成:[1,2,_,2,2,_] ，這樣就會導致2相鄰了，但是其實我們是可以使得相鄰不相同的，[2,1,2,3,2] 。

所以我們加一個限制就是，最先放數量出現最多的元素，這樣一來就能保證相鄰不相等了。

代碼如下：

class Solution {
public:vector<int> rearrangeBarcodes(vector<int>& barcodes) {unordered_map<int,int> hash;int maxnum = barcodes[0];for(auto x : barcodes) {hash[x]++;if(x != maxnum && hash[x] > hash[maxnum]) maxnum = x;}//然后開始放元素//先把maxnum放完int cnt = hash[maxnum];hash.erase(maxnum);int i = 0 , n = barcodes.size();for(; i < n && cnt--; i += 2){barcodes[i] = maxnum;}//放完maxnum開始放剩余元素for(auto& [x,cnt] : hash){while(cnt--){if(i >= n) i = 1;//偶數放完放奇數barcodes[i] = x;i+=2;}}return barcodes;}
};

29?重構字符串

https://leetcode.cn/problems/reorganize-string/

題目解析：給定一個字符串，對其進行重新排列，使得所有相鄰元素不相等。

本題和上一題類似，但是不保證有解，什么時候無解呢？出現次數最多的元素比 (size()+1)/2還大，如果總數為偶數個，那么數量大于總數的一半就無解，如果總數為奇數個，那么大于一半加一就無解。

其余的代碼和上一題一樣，就是多了一個無解的判斷。

代碼如下：

class Solution {
public:string reorganizeString(string s) {unordered_map<char,int> hash;char maxch = s[0];for(auto ch : s){hash[ch]++;if(ch != maxch && hash[ch] > hash[maxch]) maxch = ch;}int n = s.size(),i = 0,cnt = hash[maxch];if(cnt > (n+1)/2) return ""; //無解while(cnt--) {s[i] = maxch;i += 2;}hash.erase(maxch);for(auto& [ch , cnt] : hash){while(cnt--){if(i >= n) i = 1;s[i] = ch;i += 2;}}return s;}
};