此練習主要是：關于滯后補償器。
①滯后補償器作用；
②不同滯后補償器的效果；
一、為什么使用滯后補償器
- 滯后補償器：主要用于改善系統的穩態誤差；
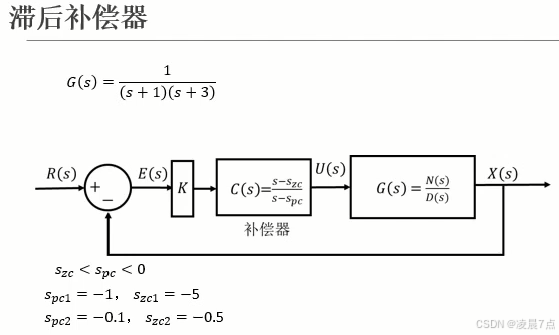
- 滯后補償器設計思路：同時為系統增加一個極點和零點，與超前補償器不同的是，滯后補償器的極點的位置比零點更加靠近虛軸；
- 選取兩組不同滯后補償器，如圖所示；
- 因為，兩組滯后補償器，零點極點的比值是一致的，所以改善穩態誤差的效果是一致的；但是，由于位置很不同，所以對系統的瞬態響應有很大影響。
- 在matlab中，繪制對應的根軌跡，以及閉環系統的單位階躍響應。
- 代碼如下：
clc;clear;close all;
%% 定義G(s)
s = tf('s');
G_s = 1/((s+1)*(s+3));
K = 2;
t = 0:0.1:20;
%% 繪制原傳遞函數根軌跡及其響應
subplot(3,2,1);
rlocus(G_s);
title('原系統根軌跡');
subplot(3,2,2);
sys_1 = feedback(K*G_s, 1);
step (sys_1,t);
title('原系統單位階躍響應');%%%% 定義補償器C1(s)
sz = -5;
sp = -1;
C1_s = (s-sz)/(s-sp);
%% 使用補償器C1(s)后的根軌跡及其響應
subplot(3,2,3);
rlocus(G_s*C1_s);
title('增加滯后補償器C1系統根軌跡');
subplot(3,2,4);
sys_2 = feedback(K*G_s*C1_s, 1);
step (sys_2,t);
title('增加滯后補償器C1系統單位階躍響應');%%%% 定義補償器C2(s)
sz = -0.5;
sp = -0.1;
C2_s = (s-sz)/(s-sp);
%% 使用補償器C1(s)后的根軌跡及其響應
subplot(3,2,5);
rlocus(G_s*C2_s);
title('增加滯后補償器C2系統根軌跡');
subplot(3,2,6);
sys_3 = feedback(K*G_s*C2_s, 1);
step (sys_3,t);
title('增加滯后補償器C2系統單位階躍響應');
二、運行結果及分析
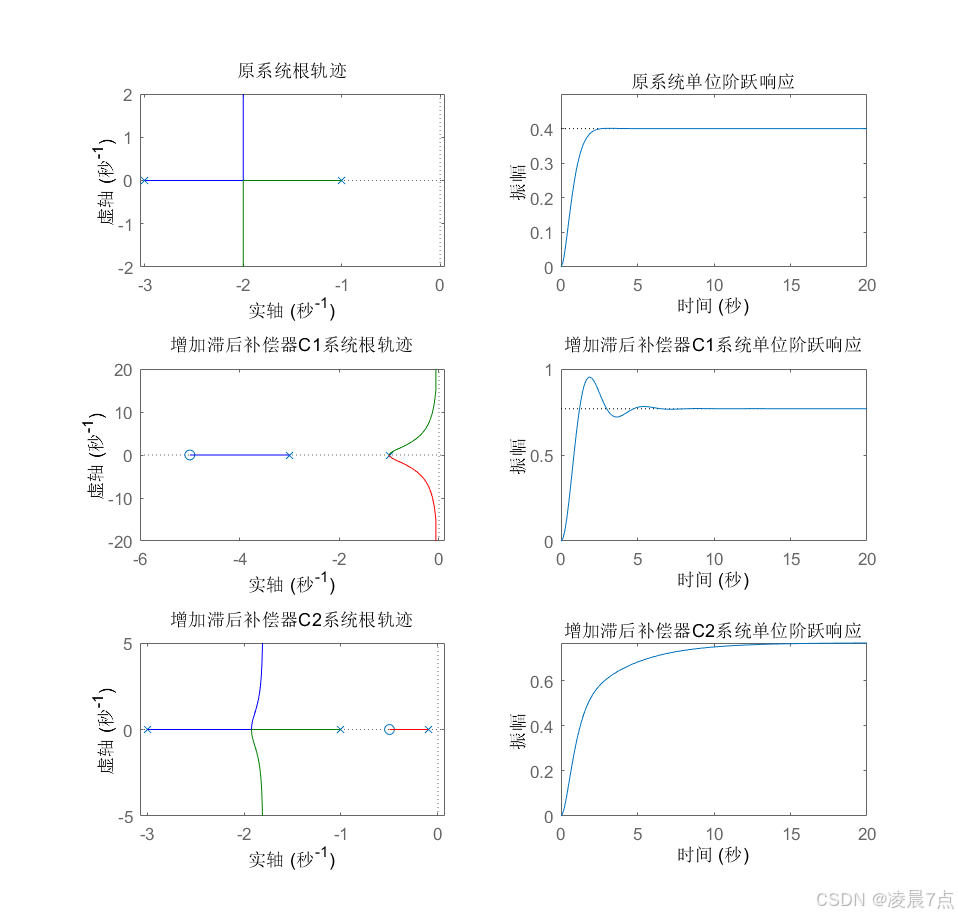
1、從原系統圖：
- 原系統單位階躍響應，最終將系統穩定在0.4左右，所以穩態誤差是1-0.4=0.6；
2、增加補償器C1系統圖：sz=-5；sp=-1；
- 增加C1補償器系統單位階躍響應，最終將系統穩定在0.8左右，所以穩態誤差是1-0.8=0.2；
- 當增加C1：sz=-5；sp=-1；此時完全改變了原因系統的根軌跡方向，因此，此時的單位階躍響應就會與原系統很不同；
3、增加補償器C2系統圖：sz=-0.5；sp=-0.1；
- 增加C2補償器系統單位階躍響應，最終將系統穩定在0.8左右，所以穩態誤差是1-0.8=0.2；
- 當增加C2：sz=-0.5；sp=-0.1；此時只是增加了一條由x=-0.1指向x=-0.5的根軌跡，對原來根軌跡影響比較小，當前根軌跡還很一致，只是增加一條距離虛軸很近的根軌跡，因此，此時的單位階躍響應就會與原系統比較類似；
4、總體來看
-
發現，增加C1和C2滯后補償器，最后的曲線截然不同。
-
當增加C1滯后補償器，就完全不同了，sz=-5；sp=-1；這對零極點就完全改變原有根軌跡的形態了，所以響應也就完全不同。
-
當增加C2滯后補償器，可以看出，從0上升到0.4的過程，幾乎和原系統一致，只是從0.4之后，再通過sz=-0.5；sp=-0.1；這對零極點來修正穩態誤差。
學習來源：《控制之美》[卷1]，王天威
)
